Движение в кулоновском поле

14.1. Принцип причинности в классической и квантовой механике

В классической механике состояние системы задается с помощью координат и скоростей частиц. Зная начальное значение координат и скоростей можно с помощью уравнения второго закона Ньютона рассчитать состояние системы в любой последующий момент времени, т.е. точно определить координаты и скорости всех частиц.

В квантовой механике состояние системы описывается волновой функцией. Если известна волновая функция в начальный момент времени, то из уравнения Шредингера

(14.1)

можно найти волновую функцию системы в любой последующий момент времени.

Одномерное уравнение Шредингера для стационарного состояния в случае свободной частицы

. (14.2)

Запишем уравнение (14.2) в виде

,

где .

Решение уравнения

,

где с₁ и с₂ - произвольные постоянные, представляет собой линейную комбинацию двух волн де Бройля.

Положим , тогда

. (14.3)

14.2. Движение частицы в одномерном потенциальном ящике с бесконечно высокими стенками

Уравнение для стационарных состояний частицы, движущейся в силовом поле с потенциальной энергией U(r)

. (14.4)

Потенциальная энергия частицы в «ящике»:

Найдем решение уравнения (14.4) при условии

.

Введем ограничение

,

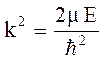отсюда

.

Решение будем искать в виде

y = с₁coskx +c₂sinkx.

На границах ящика, при x = 0 и x = a:

y(x) = 0.

Отсюда находим: y(0) = с₁ = 0,

y(а) = c₂sinka = 0.

Отсюда следует:

ka = np,

где .

Собственные волновые функции

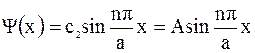. (14.5)

При x < 0, x > a y(x) = 0.

Собственные значения

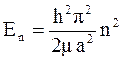, (14.6)

где n =1,2,...

Плотность вероятности обнаружить частицу в ящике

.

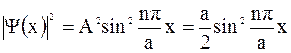Постоянную А находим из условия нормировки волновых функций

,

,

отсюда

.

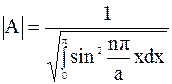Постоянная А зависит от координаты частицы и квантового числа n, характеризующего уровень энергии.

Собственная волновая функции и собственная энергия частицы в бесконечном прямоугольном ящике дискретны.

Наименьшее значение энергии частицы

.

14.3. Движение в поле с центральной симметрией

В уравнении (14.4) запишем оператор Лапласа в сферических координатах:

.

где - оператор квадрата момента импульса.

Получим уравнение Шредингера

. (14.7)

Решение будем искать в виде

y(r,q,j) = R(r)Y_lm(q,j), (14.8)

где R(r) - радиальная часть волновой функции;

Y_lm(q,j) - угловая часть волновой функции;

l, m - азимутальное и магнитное квантовое числа, соответственно.

Подставим (14.8) в уравнение (14.7). Учитывая, что

,

получим уравнение для радиальной части волновой функции

.

Введем вместо функции R(r) функцию c(r)

.

Для c(r) находим уравнение

.

При r = 0 волновая функция должна быть конечной, отсюда c(0) = 0. Введем эффективную потенциальную энергию

,

где вторая часть выражения называется центробежной энергией.

Уравнение (14.7) свелось к уравнению одномерного движения с эффективной потенциальной энергией

. (14.9)

Радиальная составляющая волновой функции R(r) зависит от вида потенциальной энергии.

Угловая часть Y_lm(q,j) определяется величиной момента импульса (азимутальное квантовое число l) и его проекцией на ось z (магнитное квантовое число m).

Состояния с заданным моментом импульса обозначаются малыми буквами латинского алфавита:

l = 0 1 2 3 4 5 6 7

s p d f g h I k

Квантовое число l определяет четность состояния. При преобразовании инверсии (отражении) волновая функция изменяется по закону

.

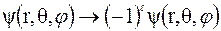Четное квантовое число соответствует четным состояниям (s,d,g,...), а при нечетном состояния (p,d,f,h,...) состояния являются нечетными.

Вероятность dW(q,j) обнаружить частицу в телесном угле dW в направлении, определяемом углами q,j:

.

Состояние с l = 0 (s - состояние) обладает сферической симметрией

.

В p - состоянии (l = 1) распределение вероятности

,

.

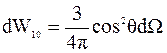Таким образом, можно сделать общие заключения о поведении волновой функции, не указывая конкретный вид потенциальной энергии U(r).

14.4. Движение в кулоновском поле

Потенциальная энергия электрона, движущегося в поле ядра с зарядом Ze

.

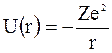Уравнение Шредингера для радиальной функции

.

Найдем энергии состояний, принадлежащих дискретному энергетическому спектру. Эти состояния соответствуют движению электрона в атоме, E < 0:

(14.10)

Здесь n = n_r + l + 1 - главное квантовое число;

n_r - радиальное квантовое число;

l - азимутальное квантовое число.

Эта формула получена Н.Бором, опиравшимся на постулаты.

Современная квантовая механика позволяет определить дискретные энергетические уровни в атоме водорода и водородоподобных атомах, не постулируя квантованность момента импульса.

Контрольные вопросы:

1. Принцип причинности в классической и квантовой механике.

2. Как описывается в квантовой механике состояние системы?

3. Какие квантовые числа отвечают дискретным значениям момента импульса?

4. Движение частицы в одномерном потенциальном ящике с бесконечно высокими стенками.

5. Собственная волновая функции и собственная энергия частицы в бесконечном прямоугольном ящике.

6. В чем заключается физический смысл процедуры нормирования волновой функции?

7. Уравнение Шредингера для радиальной функции. Движение в поле с центральной симметрией. Движение в кулоновском поле.

8. Потенциальная энергия электрона, движущегося в поле ядра.

Список литературы

1. Детлаф, А.А. Курс физики: учебное пособие для втузов / А.А. Детлаф, Б.М. Яворский. -М.: Высш. школа, 1989.- 608 с.

2. Савельев, И.В. Курс общей физики для втузов: учеб. пособие. В 5 кн. Кн. 3, 4, 5 / И.В. Савельев.- 4-е изд., перераб. - М.: Наука. Физматлит. 1998.

3. Парселл, Э. Электричество и магнетизм. В 2 т. Т 1.2. Пер. с англ. / Э. Парселл. -М.: Наука, 1975.

4. Джанколи, Д. Физика. В 2 т. Т 1.2. Пер. с англ. / Д. Джанколи. - М.: Мир, 1989.

5. Орир, Дж. Физика: В 2 т. Т 1.2. Пер. с англ. / Дж. Орир. - М.: Мир, 1981.

6. Храмов, Ю.А. Физики: биографический справочник / Ю.А. Храмов; под ред. А.И. Ахиезера.-2-е изд., исправл. и доп.- М.: Наука, 1983. – 399 с.

СОДЕРЖАНИЕ

ГЛАВА 1. Магнитное поле в вакууме.. 3

1.1. Магнитные явления. 3

1.2. Магнитная индукция. 6

1.3. Принцип суперпозиции полей. 8

1.4. Взаимодействие проводников с токами. 9

1.5. Закон Ампера. 11

ГЛАВА 2. Магнитное поле движущегося заряда и проводников с токами в вакууме.. 14

2.1. Магнитное поле движущегося заряда. 14

2.2. Закон Био-Савара-Лапласа. 16

2.3. Магнитная индукция поля прямолинейного проводника с током. 17

2.4. Магнитная индукция на оси кругового проводника с током. 19

ГЛАВА 3. Закон полного тока для магнитного поля в вакууме 22

3.1. Теорема о циркуляции. Магнитное поле соленоида с током. 22

3.2. Магнитный поток. Теорема Остроградского-Гаусса для вектора магнитной индукции. 25

3.3. Магнитный момент кругового тока. 25

3.4. Контур с током в магнитном поле. 27

3.5. Работа перемещения проводника с током в постоянном магнитном поле 30

ГЛАВА 4. Магнитное поле в веществе.. 33

4.1. Магнитные свойства вещества. 33

4.2. Атом в магнитном поле. 36

4.3. Намагниченность. Напряженность магнитного поля. 38

4.4. Магнитная проницаемость и магнитная восприимчивость. 39

4.5. Диамагнетики, парамагнетики, ферромагнетики. 40

4.6. Зависимость намагниченности от температуры. Точка Кюри. 42

ГЛАВА 5. Электромагнитная индукция.. 45

5.1. Явление электромагнитной индукции. 45

5.2. Основной закон электромагнитной индукции. 48

5.3. Закон Фарадея. 53

5.4. Правило Ленца. 54

5.5. Генератор электрического тока и электромотор. 55

5.6. Самоиндукция. Индуктивность. Замыкание и размыкание электрической цепи 56

5.7. Взаимная индукция. 59

5.8. Энергия магнитного поля. 62

ГЛАВА 6. Уравнения Максвелла.. 65

6.1. Уравнения Максвелла для постоянных электрических и магнитных полей 65

6.2. Ток смещения. 67

6.3. Полная система уравнений Максвелла. 69

6.4. Электромагнитные волны. Связь между оптическими явлениями и теорией электромагнитного поля. 71

ГЛАВА 7. Движение заряженных частиц в электрическом и магнитном полях.. 77

7.1. Движение заряженных частиц в однородном постоянном электрическом поле 77

7.2. Движение заряженных частиц в однородном постоянном магнитном поле 81

7.3. Движение заряженных частиц в постоянных однородных электрическом и магнитном полях. 82

ГЛАВА 8. Интерференция света.. 86

8.1. Монохроматичность и когерентность волн. 86

8.2. Интерференция света от двух когерентных источников. Опыт Юнга 88

8.3. Многолучевая интерференция. 91

8.4. Интерференция света в тонких пленках. 94

8.5. Кольца Ньютона. 96

ГЛАВА 9. Дифракция света.. 98

9.1. Принцип Гюйгенса – Френеля. 98

9.2. Метод зон Френеля. 101

9.3. Дифракция Фраунгофера на щели. 103

9.4. Дифракционная решетка. 106

9.5. Дифракция Френеля на круглом отверстии. 110

9.6. Дифракция на пространственной решетке. 114

ГЛАВА 10. Поляризация света.. 116

10.1. Поляризация света. 116

10.2. Поляризация при отражении и преломлении света. Закон Брюстера. Степень поляризации. 120

10.3. Поляризация при двойном лучепреломлении. 123

10.4. Анализ поляризации света. Закон Малюса. 128

10.5. Поляризационные приборы: призма Николя, стопа Столетова, поляроидные пленки. 130

10.6. Вращение плоскости поляризации. Искусственная оптическая анизотропия. Интерференция поляризованных лучей. 133

ГЛАВА 11. ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ... 138

11.1. Взаимодействие света с веществом. 138

11.2. Рефракция света. 140

11.3. Рассеяние света. 142

11.4. Поглощение света. 147

11.5. Дисперсия света. 150

ГЛАВА 12. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ И ЛЮМИНЕСЦЕНЦИЯ.. 154

12.1. Равновесное излучение. 154

12.2. Тепловое излучение абсолютно черного тела. Закон Кирхгофа. 156

12.3. Закон Стефана-Больцмана. Закон Вина. 157

12.4. Закон Рэлея-Джинса. Формула Планка. 159

12.5. Люминесценция и люминесцентный анализ 162

ГЛАВА 13. КВАНТОВЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ.. 170

13.1. Корпускулярно-волновой дуализм. 170

13.2. Фотоэффект.. 171

13.3. Эффект Комптона. 174

13.4. Постулаты Бора. Принцип неопределенности Гейзенберга. 176

ГЛАВА 14. УРАВНЕНИЕ ШРЕДИНГЕРА.. 179

14.1. Принцип причинности в классической и квантовой механике. 179

14.2. Движение частицы в одномерном потенциальном ящике с бесконечно высокими стенками. 180

14.3. Движение в поле с центральной симметрией. 182

14.4. Движение в кулоновском поле. 185

Список литературы... 187

Содержание.. 188

Поиск по сайту: