Люминесцентный анализ

При исследовании регистрируется собственное свечение объекта, либо свечение специальных люминофоров, которыми обрабатывался объект.

Люминесцентный анализ включает в себя химический и сортовой анализ. В химическом анализе наличие и концентрация примесей определяется по виду спектра и интенсивности излучения. Чувствительность химического люминесцентного анализа позволяет обнаруживать до 10^-10 – 10^-11 г/см³. Люминесцентный анализ применяют для определения подлинности документов, обнаружения следов токсических веществ, в реставрационных работах. К люминесцентному анализу относится также люминесцентная дефектоскопия (т.е. обнаружение дефектов в структуре вещества) и регистрация элементарных частиц с помощью сцинтилляционного счетчика.

Контрольные вопросы:

1. Чем отличается тепловое излучение от люминесценции?

2. Каковы источники энергии при люминесцеции?

3. Законы теплового излучения.

4. Радиолюминофоры и их применение.

5. Рентгенолюминофоры.

6. Органические люминофоры.

7. Электролюминофоры.

8. Какие люминофоры применяют в кинескопах цветного изображения?

ГЛАВА 13. КВАНТОВЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ

13.1. Корпускулярно-волновой дуализм

13.2. Фотоэффект

13.3. Эффект Комптона

13.4. Постулаты Бора. Принцип неопределенности Гейзенберга

13.1. Корпускулярно-волновой дуализм

К середине XIX в. волновая природа света было доказана теоретически и подтверждена экспериментально. Из уравнений Максвелла для электромагнитного поля можно получить уравнение для электромагнитной волны.

Решение этого уравнения имеет вид плоской волны, распространяющейся вдоль оси х:

(13.1)

где Е, Н – напряженность электрического и магнитного поля;

– амплитуда волны;

- частота;

k - волновое число;

- начальная фаза.

В конце XIX в. появились экспериментальные результаты, теоретическое обоснование которых потребовало возвращения к корпускулярному представлению.

Тепловое излучение тел в области больших частот не могло найти объяснения в классической физике. Появилась необходимость ввести понятие кванта излучения с энергией , где постоянная Планка с.

Излучение атома происходит в результате перехода электрона из одного энергетического состояния в другое. Разность энергий электронов равна энергии излученного кванта

. (13.2)

Излучение может взаимодействовать с атомом, в результате этого энергия поглощается или рассеивается.

Двойственная природа света получила название корпускулярно-волнового дуализма.

13.2. Фотоэффект

Г. Герц в 1887 г. открыл явление фотоэффекта, представляющего собой вырывание связанных в атоме электронов под действием электромагнитного излучения. На рис. 13.1 приведена схема опытов А.Г. Столетова для наблюдения фотоэффекта. Металлические пластины А и В помещены в колбу, из которой откачан воздух. Пластина В подвергается действию света. Из нее вылетают электроны, которые попадают на пластину А. В цепи течет ток, который измеряется с помощью гальванометра G. Напряжение между пластинами можно регулировать с помощью потенциометра П.

Рис. 13.1.

Зависимость фототока i от интенсивности света I приведена на рис. 13.2.

Сила тока пропорциональна числу вылетающих электронов, а поскольку интенсивность света линейно зависит от фототока, то можно сформулировать первый закон фотоэффекта:

Число электронов, вырываемых светом, прямо пропорционально интенсивности света.

Если изменить напряжение U между пластинами, то оказывается, что в цепи ток течет даже при отрицательном и равном нулю напряжении. При положительных значениях напряжения (U > 0) ток в цепи не прекращается, пока напряжение не достигнет значения U = , где – запирающий потенциал. Максимальная кинетическая энергия фотоэлектронов связана с запирающим потенциалом соотношением:

. (13.3)

Рис. 13.2.

На рис. 13.3 показана зависимость фототока i от разности потенциалов между электродами U. При увеличении интенсивности света от 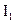до 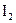, и прежней частоте, запирающий потенциал имеет то же самое значение, следовательно, не изменяется максимальная кинетическая энергия фотоэлектронов. Первый закон фотоэффекта находится в согласии с классическими представлениями.

Рис. 13.3.

Второй закон фотоэффекта:

Максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности света.

Второй закон фотоэффекта не укладывался в рамки классических представлений, т.к. интенсивность излучения была пропорциональна квадрату амплитуды электромагнитной волны, следовательно, пропорциональна энергии излучения. Поэтому чем большую энергию имеет излучение, тем больше должна быть кинетическая энергия электронов.

Запирающий потенциал зависит не от интенсивности излучения I, а от его частоты.

Третий закон фотоэффекта:

Существует наименьшая частота, зависящая от вещества пластины и называемая красной границей фотоэффекта, при которой еще возникает фотоэффект.

Классическая физика не могла дать объяснение третьему закону фотоэффекта ни для свободных, ни для связанных электронов. Теоретическое обоснование фотоэффекта было дано Альбертом Эйнштейном в 1905 году. Для объяснения фотоэффекта необходимо было введение представления о свете как о частице, что послужило началом создания квантовой механики.

Эйнштейн Альберт (1879-1955), выдающийся физик-теоретик. Родился в Ульме. Окончил Цюрихский политехникум. Создатель специальной и общей теории относительности, квантовой теории.

Свет в данном эффекте следует рассматривать как поток квантов с энергией , поглощаемых электронами. Максимальная энергия электрона 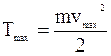находится из уравнения Эйнштейна для фотоэффекта:

, (13.4)

где А – работа выхода электрона из электрода в вакуум.

13.3. Эффект Комптона

Квантовые свойства электромагнитного излучения особенно наглядно проявляются в эффекте Комптона.

Комптон Артур Холли (1892-1962), американский физик. Родился в Вустере (штат Огайо). Окончил Принстонский университет. Работы посвящены атомной и ядерной физике, физике космических лучей.

В 1922 г. Комптон открыл явление изменения длины волны рентгеновского излучения вследствие рассеяния его электронами вещества. Длина волны рассеянного излучения возрастает с увеличением угла наблюдения. Поскольку рассеяние происходит на свободных электронах вещества, то эффект изменения длины волны не зависит от характеристик вещества.

Объяснение было получено с помощью модели упругого рассеяния квантов рентгеновского излучения на покоящихся электронах. Если рассматривать излучение как частицы, то можно применить законы сохранения энергии и импульса:

(13.5)

. (13.6)

где - начальный импульс кванта;

- импульс рассеянного кванта;

- импульс электрона после рассеяния;

- энергия покоя электрона;

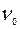- начальная частота кванта;

- частота рассеянного кванта.

Перенесем вектор импульса р в левую часть уравнения (13.5) и найдем квадрат импульса электрона:

. (13.7)

Импульсы квантов до и после рассеяния:

, (13.8)

. (13.9)

В выражение (13.7) подставим (13.8) и (13.9) и умножим полученное выражение справа и слева на :

. (13.10)

Из закона сохранения энергии (13.5) находим:

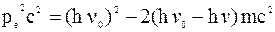, (13.11)

Приравнивая правые части уравнений (13.10) и (13.11), получим

= , (13.12)

Из (13.13) получим энергию кванта после рассеяния:

. (13.13)

Изменение длины волны связано с углом рассеяния соотношением:

, (13.14)

где 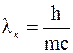- комптоновская длина волны электрона.

Тепловое излучение в ультрафиолетовой области спектра и эффект Комптона свидетельствовали о корпускулярных свойствах излучения.

13.4. Постулаты Бора. Принцип неопределенности Гейзенберга

Необходимость создания квантовой механики возникла особенно остро при попытках дать объяснение опытам Резерфорда по рассеянию - частиц на мишенях из тонкой фольги.

Резерфорд Эрнест (1871-1937), английский физик. Родился в Брайтеуотере (Новая Зеландия). Окончил Кентерберийский колледж Новозеландского университета. Исследования посвящены радиоактивности, атомной и ядерной физике.

Часть частиц проходила через фольгу, а некоторые частицы рассеивались на фольге, причем угол рассеяния мог достигать . Это явление можно было объяснить, если предположить, что в центре атома находиться ядро, создающее сильное кулоновское поле. Планетарная модель атома была устойчивой с точки зрения классической механики, но противоречила классической электродинамике.

В планетарной модели предполагалось, что электроны вращаются вокруг ядра, поэтому должны излучать электромагнитные волны. Энергия электронов при этом уменьшается, в результате чего они должны «упасть на ядро». Кроме того, согласно экспериментальным данным спектроскопии, атом может излучать не на любой частоте, а на строго определенных частотах, характерных для каждого атома. Возникли противоречия с классической физикой, которые были преодолены Нильсом Бором.

Нильс Бор (1885-1962), датский физик-теоретик. Родился в Копенгагене. Закончил Копенгагенский университет. Бор является основоположником квантовой физики. Создал квантовую модель атома и сформулировал принципы соответствия. Один из создателей капельной модели ядра. Создал большую школу физики.

Постулаты Бора:

1. Атом может излучать или поглощать энергию при переходе из одного стационарного состояния в другое. Частота света связана с разностью энергии атома в стационарных состояниях:

.

2. Могут существовать только такие орбиты, на которых момент импульса электрона L равен целому кратному постоянной Планка : .

Теория Бора была еще недостаточно последовательной, т.к. предполагала существование классических орбит электронов. Чтобы определить траекторию электрона, необходимо точно знать координату и импульс частицы в каждый момент времени. Это противоречит принципу неопределенности Гейзенберга:

Произведение неопределенностей в измерении координаты и импульса должно быть больше постоянной Планка:

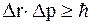. (13.15)

Гейзенберг Вернер Карл (1901-1976), немецкий физик-теоретик. Родился в Вюрцбурге. Окончил Мюнхенский и Геттингенский университеты. Работы относятся к квантовой механике, квантовой электродинамике, релятивистской квантовой теории поля, теории ядра. В 1925 году разработал матричную механику. Вслед за Д.Д.Иваненко пришел к протонно-нейтронной модели ядра.

В квантовой механике существуют и другие дополнительные физические величины, которые должны удовлетворять принципу неопределенности Гейзенберга, например, энергия и время:

. (13.16)

Доказательством справедливости принципа неопределенности является стабильность атома. Если электрон «упадет на ядро», то его координата станет точно известной, т.е. он будет находиться на расстоянии от центра ядра. Импульс покоящегося электрона также известен точно: р = 0. Отсюда следует, что , что противоречит принципу неопределенности.

Постулаты Бора и принцип неопределенности в современной квантовой механике являются следствиями волновой теории, разработанной Л. де Бройлем, Э. Шредингером, В. Гейзенбергом, П. Дираком и др.

Контрольные вопросы:

1. Чем была вызвана необходимость возвращения к корпускулярной теории света и введения понятия «квант излучения»?

2. Законы фотоэффекта и их роль в развитии квантовой механики?

3. Изменение длины волны рентгеновского излучения вследствие рассеяния его электронами вещества.

4. Постулаты Бора.

5. Принцип неопределенности Гейзенберга.

6. Принцип неопределенности в современной квантовой механике.

ГЛАВА 14. УРАВНЕНИЕ ШРЕДИНГЕРА

14.1. Принцип причинности в классической и квантовой механике

Поиск по сайту: