Теорема о циркуляции

Циркуляция магнитной индукции поля в вакууме по замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром.

В дифференциальной форме теорема о циркуляции:

,

где j - вектор плотности тока.

Найдем с помощью теоремы о циркуляции магнитную индукцию на оси соленоида с током, длина которого во много раз больше диаметра его витков. Такой соленоид называется бесконечным или тонким.

Магнитное поле бесконечного соленоида сосредоточено внутри него и равно нулю вне соленоида. Проведем контур 12341, который охватывает n витков соленоида (рис.3.2). Найдем циркуляцию вектора B по замкнутому контуру:

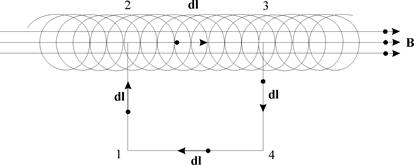
Рис. 3.2.

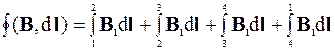. (3.4)

На участках 1-2 и 3-4 контур перпендикулярен к силовым линиям поля, поэтому проекция магнитной индукции на направление элемента контура . На участке 4-1 вне соленоида 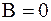, следовательно циркуляция вектора В по замкнутому контуру:

.

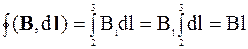Согласно теореме о циркуляции для n токов:

.

Отсюда находим магнитную индукцию бесконечного соленоида:

, (3.5)

где - число витков на единицу дины соленоида.

3.2. Магнитный поток. Теорема Остроградского-Гаусса для вектора магнитной индукции

Потоком вектора магнитной индукции В через произвольную поверхность S называется величина:

, (3.6)

где 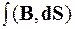- интеграл по некоторой поверхности S от вектора магнитной индукции.

Поток вектора В через замкнутую поверхность численно равен разности числа выходящих и входящих силовых линий:

. (3.7)

Поскольку отсутствуют магнитные заряды, на которых могли бы начинаться или заканчиваться силовые линии, следовательно, число выходящих линий равно числу входящих:

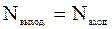, (3.8)

поэтому

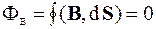. (3.9)

Теорема Остроградского-Гаусса для вектора магнитной индукции:

Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю.

3.3. Магнитный момент кругового тока

Магнитную индукцию в центре кругового тока можно представить в виде:

, (3.10)

где S = pR² - площадь, обтекаемая током.

Магнитным моментом плоского замкнутого контура с током называется вектор:

P_m = IS n,

где S – площадь поверхности, ограниченной контуром;

n - единичный вектор нормали к плоскости контура.

Направление вектора совпадает с направлением нормали n к плоскости кругового тока.

Выразим магнитную индукцию В через магнитный момент :

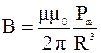. (3.11)

Рис. 3.3.

Вектор магнитного момента имеет то же направление, что и магнитная индукция В, следовательно, направление магнитного момента можно также определить по правилу правого винта (рис. 3.3).

Магнитный момент плоского контура произвольной формы с током также можно найти по формуле

P_m = IS. (3.12)

Магнитное поле плоского контура произвольной формы на расстояниях, больших по сравнению с размером системы, можно представить в виде рис. 3.4. Для сравнения на этом рисунке приведено графическое изображение электрического поля диполя, подобное магнитному полю контура с током.

Рис. 3.4.

, (3.13)

где q - угол между вектором и вектором r, проведенным из центра контура в данную точку поля А.

Магнитное поле на оси кругового тока ():

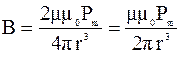. (3.14)

3.4. Контур с током в магнитном поле

Если контур с током поместить в магнитное поле, то на него, согласно закону Ампера, будет действовать механическая сила:

. (3.15)

Рассмотрим прямоугольный проволочный контур с током. Магнитное поле направлено, как показано на рис. 3.5. Силы и 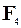равны нулю, т.к. sin a = 0, где a - угол между направлением тока и вектором В.

Силы и отличны от нуля и направлены в противоположные стороны перпендикулярно плоскости рисунка.

Рис. 3.5.

Силы, приложенные к сторонам 1 и 3, образуют пару сил, следовательно, возникает крутящий механический момент:

, (3.16)

где n - единичный вектор, направленный вдоль нормали к контуру;

S - площадь контура.

Модуль механического момента:

,

где j - угол между вектором магнитного момента P и вектором B.

Найдем механический момент при различных углах j:

1. j = 0, M_кр= 0. Магнитные силы растягивают контур в его плоскости (рис. 3.6).

Рис. 3.6.

2. . Крутящий момент имеет наибольшее положительное значение и будет стремиться повернуть контур таким образом, чтобы векторы P_m и B имели одинаковое направление (рис. 3.7).

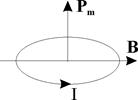
Рис. 3.7.

3. j = p, М_кр= 0. Магнитные силы сжимают контур (рис. 3.8).

Рис. 3.8.

4. . Крутящий момент принимает отрицательное значение (рис.3.9).

Рис. 3.9.

Контур с током в магнитном поле обладает потенциальной энергией:

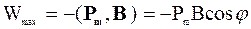. (3.17)

Рассмотрим следующие случаи:

1. j = 0, W_min = - P_mB;

2. , W = 0;

3. j = p, W_max = P_mB ;.

4. 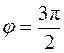, W= 0.

Максимальное значение W_max = P_mB имеет потенциальная энергия контура с током, если векторы P_m и B направлены в противоположные стороны и минимальное значение W_min = - P_mB в случае, если они одинаково направлены. Минимум потенциальной энергии соответствует положению устойчивого равновесия.

3.5. Работа перемещения проводника с током в постоянном магнитном поле

Пусть контур с током находится в магнитном поле, перпендикулярном к плоскости контура. Один из проводников, образующих контур, может перемещаться (рис. 3.10).

Рис. 3.10.

Сила Ампера, действующая на подвижный проводник длиной l:

.

Направление силы определяется по правилу левой руки. Под действием силы Fпроисходит перемещение проводника на элементарную длину dh, при этом совершается элементарная работа:

,

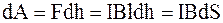где dS = ldh - заштрихованная площадь.

Eсли магнитная индукция B направлена под произвольным углом a к нормали контура, то работа записывается в виде:

.

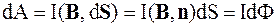Элементарная работа dA, совершаемая магнитной силой над участком контура с током, равна произведению тока на величину магнитного потока dФ через поверхность, описанную этим участком при движении.

Рассмотрим теперь произвольный контур с током в магнитном поле (рис. 3.11). Под действием силы Ампера элемент контура dl переместится на h. Работа, совершаемая над элементом контура:

.

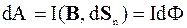где d S _n= [ h, d l ] - вектор, равный по величине площади, описанной элементом контура при перемещении и направленный вдоль положительной нормали n.

Полная работа, совершаемая магнитной силой:

, (3.18)

где Ф₁, Ф₂- магнитный поток через контур в начальном и конечном положениях.

Работа, совершаемая магнитными силами, равна произведению тока на приращение магнитного потока через контур.

Рис. 3.11.

При повороте плоского контура из положения неустойчивого равновесия (Ф₁ = - BS) в устойчивое положение (Ф₂ = BS) магнитные силы совершают над контуром работу:

A = I(BS - (-BS)) = 2IBS.

Это выражение можно также получить, пользуясь тем, что работа равна разности потенциальных энергий контура с током в магнитном поле:

A = W₁ - W₂ = P_mB - (-P_mB) = 2P_mB = 2IBS.

Магнитная сила может не только поворачивать контур, но и перемещать его на плоскости.

Магнитное поле не может совершать работы, т.к. направление перемещения заряда перпендикулярно к направлению действия силы Лоренца.

F = q[ v,B ].

Работа магнитной силы совершается за счет энергии источника тока, а не за счет энергии магнитного поля.

Контрольные вопросы:

1. Применение теоремы о циркуляции магнитной индукции для расчета магнитного поля соленоида с током.

2. Теорема Остроградского – Гаусса для вектора магнитной индукции.

3. Магнитный момент кругового тока.

4. Механический момент и потенциальная энергия контура с током в магнитном поле.

5. Элементарная работа, совершаемая магнитной силой над участком контура с током.

6. Работа магнитной силы при повороте плоского контура из положения неустойчивого равновесия в устойчивое положение.

ГЛАВА 4. Магнитное поле в веществе

4.1. Магнитные моменты атомов

4.2. Атом в магнитном поле

4.3. Намагниченность. Напряженность магнитного поля

4.4. Магнитная проницаемость и магнитная восприимчивость

4.5.Диамагнетики, парамагнетики, ферромагнетики

4.6. Зависимость намагниченности от температуры. Точка Кюри

4.1. Магнитные свойства вещества

Магнитное поле, создаваемое кольцом с током, имеет такую же структуру, как и электрическое поле, создаваемое электрическим диполем - системой двух равных по величине разноименных зарядов (рис. 3.4.).

Зависимость напряженности электрического поля от дипольного электрического момента:

, (4.1)

где - электрический момент диполя;

l - вектор, направленный по оси диполя от отрицательного заряда к положительному;

r - вектор, направленный от середины диполя в данную точку поля А;

- единичный вектор.

Модуль вектора напряженности электрического поля:

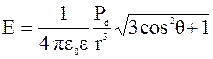, (4.2)

где q - угол между векторами P _d и r.

Магнитный дипольный момент возникает при движении заряда по окружности.

Зависимость напряженности магнитного поля H от дипольного магнитного момента имеет аналогичный вид.

, (4.3)

где P _m - дипольный магнитный момент;

r - вектор, направленный от центра витка с током в данную точку поля А (рис. 4.1).

Модуль вектора напряженности магнитного поля:

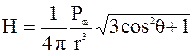, (4.4)

где q - угол между векторами P _m и r.

Рис. 4.1.

Ампер предположил, что внутри атомов и молекул существуют электрические токи, т.е. атомы и молекулы представляют собой "токовые лепестки", следовательно, могут обладать магнитным моментом.

Магнитный момент атомов и молекул измеряется в единицах элементарного магнитного момента - магнетона Бора:

, (4.5)

где e, m_e - заряд и масса электрона;

, h - постоянная Планка, .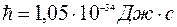

Орбитальный магнитный момент электрона связан с его моментом импульса L _e соотношением:

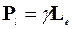, (4.6)

где 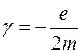- гиромагнитное отношение;

;

l – орбитальное квантовое число.

Орбитальный магнитный момент атома складывается из магнитных моментов всех электронов атома:

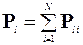. (4.7)

Электрон обладает также собственным магнитным моментом, который обусловлен наличием у электрона собственного механического момента (спина).

Собственный магнитный момент электрона связан с его собственным моментом импульса соотношением:

, (4.8)

где - гиромагнитное отношение;

;

S - спиновое квантовое число.

Гиромагнитное отношение 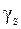в два раза больше орбитального гиромагнитного отношения электрона:

.

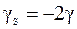Собственный магнитный момент атома:

,

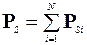Полный магнитный момент атома складывается из орбитального и собственного моментов

P = P _l + P _S. (4.9)

Если в атоме имеются спаренные электроны, то орбитальные магнитные моменты направлены противоположно друг другу. Собственные магнитные моменты также антипараллельны. В результате суммарный магнитный момент атома равен нулю.

Если в атоме имеется неспаренный электрон, то суммарный магнитный момент атома отличен от нуля. Такие атомы называются магнитными.

4.2. Атом в магнитном поле

В магнитном поле на замкнутый орбитальный ток I, вызванный движением электрона в атоме, действует вращающий момент:

, (4.10)

где угловая скорость

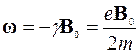. (4.11)

Магнитный момент пропорционален механическому моменту и изменяется по закону:

. (4.12)

Вектор P совершает прецессионное движение (рис. 4.2.) Такое движение магнитного момента P и орбиты электрона называется прецессией Лармора.

Поиск по сайту: