 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пример 2. Замкнем электрическую цепь
Замкнем электрическую цепь. Тогда в цепи кроме э.д.с. источника тока Е возникает э.д.с. самоиндукции Еs. Из закона Ома следует:
 .
.
Отсюда находим зависимость тока от времени при замыкании цепи:
 . (5.23)
. (5.23)
На рис. 5.13 представлены графики зависимости тока при размыкании (кривая 1) и при замыкании цепи (кривая 2).
5.7. Взаимная индукция
Явление возникновения э.д.с. в одном из контуров при изменении магнитного потока через другой контур называется взаимной индукцией.
Если рядом расположены два контура с токами I1 и I2, то первый контур может оказывать влияние на второй, что связано с изменением магнитного потока через поверхность, ограниченную вторым контуром. Аналогично, второй контур оказывает воздействие на первый контур. При этом возможны следующие случаи изменения магнитного потока через контуры:
1. При изменении величин тока в одном из неподвижных контуров;
2. При изменении расстояния между контурами;
3. При повороте одного контура относительно другого;
4. При деформации контуров;
5. При введении ферромагнетиков.
Независимо от способа, которым осуществляется изменение полного магнитного потока y через поверхность контура, в нем возникает индукционный электрический ток.
Рассмотрим близлежащие неподвижные контуры при отсутствии ферромагнетиков (рис. 5.14).
Контур 1 с током I1 создает поток магнитной индукции через контур 2:
 , (5.24)
, (5.24)
где L21 - коэффициент взаимоиндуктивности.

Рис. 5.14.
При изменении тока I1 возникает изменение магнитного потока, при этом индуцируется э.д.с.:
 . (5.25)
. (5.25)
Контур 2 также создает поток магнитной индукции через контур 1:
 . (5.26)
. (5.26)
При изменении тока I2, в нем возникает э.д.с.
 . (5.27)
. (5.27)
Контуры 1 и 2 называются связанными. Коэффициенты L12 и L21 называются взаимной индуктивностью контуров. При отсутствии ферромагнетиков:
L12 = L21. (5.28)
Трансформатором называется аппарат, преобразующий на основе явления взаимной индукции переменный ток одного напряжения в переменный ток той же частоты, но другого напряжения. Трансформатор имеет не менее двух обмоток, связанных общим магнитным потоком. Обмотка трансформатора, связанная с источником тока, называется первичной, а обмотка, отдающая электроэнергию, называется вторичной.
Полный поток, или потокосцепление, через вторичную обмотку:
 . (5.29)
. (5.29)
Найдем отсюда взаимную индуктивностьL21:
 . (5.30)
. (5.30)
Аналогично находим поток через первичную обмотку  и взаимную индуктивность L12:
и взаимную индуктивность L12:
 . (5.31)
. (5.31)

Рис. 5.15.
Поскольку m ¹ 1 нельзя считать, что L12 = L21, т.к. магнитная проницаемость зависит от напряженности магнитного поля Н в сердечнике. Если число обмоток второго контура N2 < N1, то при одинаковом токе они будут создавать различную напряженность магнитного поля, отсюда следует, что э.д.с.  . Коэффициентом трансформации называется отношение э.д.с.
. Коэффициентом трансформации называется отношение э.д.с.  в первичной обмотке к э.д.с.
в первичной обмотке к э.д.с.  во вторичной обмотке:
во вторичной обмотке:
 , (5.32)
, (5.32)
где  ,
,
 . (5.33)
. (5.33)
При  трансформатор понижает напряжение:
трансформатор понижает напряжение:

Первичную и вторичную мощности трансформатора можно считать одинаковыми:
 . (5.34)
. (5.34)
Отношение токов обратно отношению напряжений:
 , (5.35)
, (5.35)
отсюда следует, что при  трансформатор повышает ток:
трансформатор повышает ток:
I2 > I1.
5.8. Энергия магнитного поля
Рассмотрим цепь, состоящую из тонкого соленоида и источника тока (рис. 5.16).
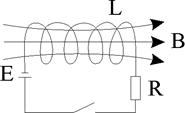
Рис. 5.16.
Пусть сначала в цепи идет ток I. Разомкнем ключ, тогда через сопротивление R будет идти постепенно убывающий ток, который поддерживается возникающей в соленоиде э.д.с. самоиндукции  . Найдем работу dA, совершаемую этим током за время dt:
. Найдем работу dA, совершаемую этим током за время dt:
 . (5.36)
. (5.36)
Если индуктивность соленоида L = const, то:
 ,(5.37)
,(5.37)
отсюда следует
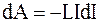 . (5.38)
. (5.38)
Найдем работу, совершаемую за время изменения тока от I до 0:
 . (5.39)
. (5.39)
Работа совершается за счет энергии магнитного поля W:
 . (5.40)
. (5.40)
Пусть теперь в начальный момент цепь разомкнута. Замкнем ключ, тогда в цепи будет нарастать ток, при этом возникает э.д.с. самоиндукции ES. Найдем работу, которую необходимо совершить против э.д.с. самоиндукции, чтобы создать магнитное поле в соленоиде:
 . (5.41)
. (5.41)
Подставляя в (5.41) индуктивность тонкого соленоида  и зависимость тока от напряженности магнитного поля I =
и зависимость тока от напряженности магнитного поля I =  , находим энергию магнитного поля:
, находим энергию магнитного поля:
 . (5.42)
. (5.42)
Плотность энергии магнитного поля, запасенной в соленоиде:
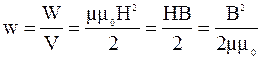 . (5.43)
. (5.43)
Контрольные вопросы:
1. Причины возникновения индукционного тока.
2. Опыты Фарадея.
3. Замыкание и размыкание электрической цепи.
4. Индуктивность.
5. Самоиндукция.
6. Взаимоиндуктивность.
7. Закон электромагнитной индукции.
8. Движение проводника с током в магнитном поле.
9. Правило правой руки.
10. Закон Фарадея. Правило Ленца.
11. Применение закона электромагнитной индукции.
12. Генератор электрического тока и электромотор.
13. Индуктивность.
14. Принцип работы трансформатора.
15. Энергия магнитного поля.
16. Генератор электрического тока.
17. Электромотор.
ГЛАВА 6. Уравнения Максвелла
6.1. Уравнения Максвелла для постоянных электрических и магнитных полей
6.2. Ток смещения
6.3. Полная система уравнений Максвелла для электромагнитного поля
6.4. Электромагнитные волны. Связь между оптическими явлениями и теорией электромагнитного поля
6.1. Уравнения Максвелла для постоянных электрических и магнитных полей
Закон электромагнитной индукции Фарадея завершил открытие ряда законов: Кулона, Ампера, Био-Савара-Лапласа.
Теоремы Остроградского-Гаусса и Стокса для постоянных электрических и магнитных полей позволили от дифференциальной формы законов:
 , (6.1)
, (6.1)
 , (6.2)
, (6.2)
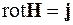 , (6.3)
, (6.3)
 , (6.4)
, (6.4)
связывающих напряженность электрического поля E, напряженность магнитного поля H, магнитную индукцию B, электрическое смещение D с плотностью заряда ρ и плотностью электрического тока j, перейти к интегральной форме законов:
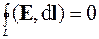 , (6.5)
, (6.5)
 , (6.6)
, (6.6)
 , (6.7)
, (6.7)
 . (6.8)
. (6.8)
На замкнутом пути в электрическом поле работа силы, действующей на заряд q, равна 0:
 .
.
Отсюда следуют уравнения (6.5, 6.1) указывающие на соленоидальный характер электрического поля.
Уравнения (6.2, 6.6) связывают возникновение электрического поля с наличием электрического заряда плотностью ρ.
Вихревой характер магнитного поля отражают уравнения (6.3, 6.7). Источником магнитного поля являются токи с плотностью j.
Уравнения (6.4, 6.8) указывают на отсутствие в природе магнитных зарядов.
При внешних схожести нет полной симметрии между уравнениями для электрического и магнитного полей. Следует отметить, что хотя найти магнитный заряд пока не удалось, но попытки восстановления симметрии полей пока не оставлены.
Уравнения для электрического и магнитного полей следует дополнить “ материальными “ уравнениями:
 , (6.9)
, (6.9)
 , (6.10)
, (6.10)
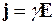 , (6.11)
, (6.11)
где g - удельная электропроводность.
Полученная система уравнений описывает электрические и магнитные взаимодействия неподвижных зарядов и постоянных токов.
6.2. Ток смещения
Физический смысл закона электромагнитной индукции заключается в том, что меняющееся во времени магнитное поле создает электрическое поле.
Электродвижущая сила Ei равна циркуляции вектора напряженности электрического поля E по замкнутому контуру L:
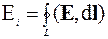 .
.
Возникновение индукционного тока связано с изменением магнитного потока:
 .
.
Изменяя порядок интегрирования и дифференцирования, находим:
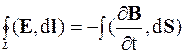 , (6.12)
, (6.12)
или в дифференциальной форме:
 . (6.13)
. (6.13)
Максвелл предположил, что изменяющееся во времени электрическое поле создает магнитное поле, циркуляция которого по замкнутому контуру:
 ,
,
где jсмещ - введенный Максвеллом ток смещения, имеющий размерность плотности тока. Сумма тока проводимости j и тока смещения jсмещ называется полным током:
 .
.
В отличие от тока смещения, ток проводимости может протекать в разомкнутой электрической цепи.
Если в цепь постоянного тока включить конденсатор, то конденсатор зарядится, между пластинами возникнет электрическое поле (рис. 6.1).

Рис. 6.1.
Между обкладками конденсатора отсутствуют носители заряда, поэтому ток прекратится.
Переменный электрический ток вызовет периодическую перезарядку конденсатора, при этом изменяется полярность пластин, направление и величина электрического поля. Этот процесс можно описать с помощью введения тока смещения, пропорционального скорости изменения электрического поля. Если между пластинами конденсатора имеется диэлектрик, то плотность тока смещения пропорциональна скорости изменения вектора электрического смещения:
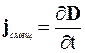 . (6.14)
. (6.14)
Уравнение (6.7) будет теперь иметь вид:
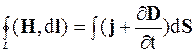 , (6.15)
, (6.15)
или в дифференциальной форме:
 . (6.16)
. (6.16)
В диэлектрике ток смещения состоит из двух слагаемых:
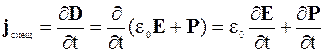 , (6.17)
, (6.17)
где  - “ истинный “ ток смещения;
- “ истинный “ ток смещения;
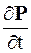 - ток поляризации.
- ток поляризации.
В вакууме вектор поляризации P = 0, но ток смещения  не равен 0, если электрическое поле изменяется во времени.
не равен 0, если электрическое поле изменяется во времени.
Максвелл Джеймс Клерк (1831 – 1879) – английский физик, родился в Эдинбурге. Учился в Эдинбургском и Кембриджском университетах. Создал Кавендишскую лабораторию в Кембридже. Работы посвящены электродинамике, молекулярной физике, общей статистике, оптике, механике, теории упругости. Создал в 1860 – 65 г.г. теорию электромагнитного поля, сформулированную в виде уравнений, носящих его имя. Ввел понятия тока смещения и дал определение электромагнитного поля, предсказал излучение электромагнитных волн движущимися зарядами. Установил связь между оптическими и электромагнитными явлениями.
6.3. Полная система уравнений Максвелла
Запишем уравнения Максвелла в дифференциальной и в интегральной формах для случая переменных электрического и магнитного полей:
 ,
,  , (6.18)
, (6.18)
 ,
,  . (6.19)
. (6.19)
 ,
, 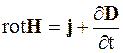 , (6.20)
, (6.20)
 ,
,  . (6.21)
. (6.21)
Уравнения Максвелла позволяют по заданным распределениям зарядов и токов, а также по заданным законам изменения электрического и магнитного полей, найти величину полей E и B в каждой точке пространства.
Плотности ρ и j связаны соотношением:
 , (6.22)
, (6.22)
или в интегральной форме:
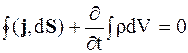 .
.
Это соотношение основано на законе сохранения заряда в замкнутой изолированной области и называется уравнением непрерывности для тока. Из условия 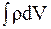 = const следует:
= const следует:

Четыре векторных уравнения Максвелла образуют систему восьми скалярных уравнений для двенадцати переменных, которые дополняются уравнением непрерывности (6.22) и материальными уравнениями (6.9 – 6.11).
Уравнения Максвелла и уравнение Лоренца, описывающее движение заряженной частицы в электрическом и магнитном полях:  , образуют фундаментальную систему уравнений.
, образуют фундаментальную систему уравнений.
Уравнения Максвелла являются феноменологическими, т.е. основаны на опытных данных.
В теории Максвелла не рассматриваются явления, происходящие в веществе на микроскопическом уровне, поэтому она является макроскопической. Поля зарядов и токов усредняются по времени.
Физической основой теории Максвелла является принцип дальнодействия электромагнитного поля. Согласно этому принципу, электромагнитное поле распространяется от источника не мгновенно, а с постоянной скоростью с, называемой скоростью света:
 .
.
Ньютон придерживался теории близкодействия, т.е. предполагал, что поле мгновенно распространяется от одного тела к другому.
Уравнения Максвелла инвариантны относительно преобразований Лоренца для электрического и магнитного полей, поэтому они являются релятивистскими уравнениями, и справедливы для описания полей, создаваемых частицами, движущимися со скоростями, близкими к скорости света.
Уравнения Максвелла справедливы во всех инерциальных системах отсчета.
6.4. Электромагнитные волны. Связь между оптическими явлениями и теорией электромагнитного поля
В случае однородной нейтральной (ρ = 0) и непроводящей ( ) среды с постоянными проницаемостями (
) среды с постоянными проницаемостями ( = const,
= const,  = const) уравнения Максвелла в дифференциальной форме имеют симметричный вид:
= const) уравнения Максвелла в дифференциальной форме имеют симметричный вид:
 (6.23)
(6.23)
Продифференцируем по времени материальные уравнения  и
и  , находим:
, находим:
 (6.24)
(6.24)
Найдем дивергенцию магнитной индукции B и электрического смещения D:
 (6.25)
(6.25)
Уравнения (6.23) с учетом (6.24) и (6.25) запишем в виде пары уравнений:
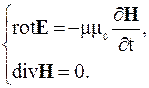 (6.26)
(6.26)
и пары уравнений:
 (6.27)
(6.27)
Эти уравнения можно преобразовать к виду волновых уравнений:
 (6.28)
(6.28)
где  - оператор Лапласа;
- оператор Лапласа;
с =  - скорость света.
- скорость света.
В декартовой системе координат:
 (6.29)
(6.29)
Найдем волновые уравнения и их решения для случая плоской электромагнитной волны.
Пусть в нейтральной ( ), непроводящей среде с постоянными проницаемостями (
), непроводящей среде с постоянными проницаемостями ( ) вдоль оси х распространяется волна
) вдоль оси х распространяется волна  .
.
Уравнения (6.23) в скалярной форме будут иметь вид:
 (6.30)
(6.30)
Здесь использовались условия, справедливые для плоской волны:  не зависят от координаты на оси х, вдоль которой распространяется волна; они могут быть отличны от нуля только в том случае, если вдоль оси х накладываются однородные постоянные поля
не зависят от координаты на оси х, вдоль которой распространяется волна; они могут быть отличны от нуля только в том случае, если вдоль оси х накладываются однородные постоянные поля  .
.
Отсюда следует, что 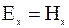 = 0, поэтому векторы напряженности электрического и магнитного полей перпендикулярны к оси х.
= 0, поэтому векторы напряженности электрического и магнитного полей перпендикулярны к оси х.
Получим уравнения:
 (6.31)
(6.31)
 (6.32)
(6.32)
Пусть вначале создана компонента электрического поля  . Изменение во времени этого поля вызовет появление переменного магнитного поля
. Изменение во времени этого поля вызовет появление переменного магнитного поля  . Напомним, что
. Напомним, что 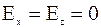 ,
, 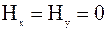 .
.
Продифференцируем уравнения (6.31) по х:
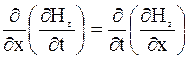 ,
,  .
.
Получим волновые уравнения для компонент электромагнитного поля  и
и  :
:
 (6.33)
(6.33)
Из уравнений (6.33) следует, что вектор E в плоской электромагнитной волне перпендикулярен вектору H. Эти векторы лежат в плоскости, перпендикулярной к направлению распространения волны (рис. 6.2).
Решение уравнений (6.33):

где w - циклическая частота волны;
 - волновое число;
- волновое число;
 - фазовая скорость волны;
- фазовая скорость волны;
 - скорость электромагнитной волны в вакууме;
- скорость электромагнитной волны в вакууме;
 - начальная фаза колебаний;
- начальная фаза колебаний;
 ,
,  - амплитуды переменных электрического и магнитного полей.
- амплитуды переменных электрического и магнитного полей.

Рис. 6.2.
В вакууме (e = 1, m = 1) фазовая скорость волны v совпадает со скоростью света c.
Максвеллу принадлежит заслуга установления связи между электромагнитными и оптическими явлениями. Он предположил, что свет - электромагнитные волны в видимом диапазоне частот излучения.
Г.Герц экспериментально доказал в 1888 г. существование электромагнитных волн.
Плоская электромагнитная волна является монохроматической, т.к. проекции электрического и магнитного полей на оси, перпендикулярные к оси x, вдоль которой распространяется волна, совершают гармонические колебания с одинаковой частотой w.
Электромагнитные волны являются поперечными, в отличие от механических волн в среде, которые могут быть как продольными, так и поперечными.
Для распространения механических волн необходима среда, частицы которой приходят в движение и передают возмущение от точки к точке. Вначале Максвелл также предполагал, что для распространения электромагнитных волн нужна особая среда - эфир, но позже он отказался от этой теории.
Электромагнитная волна может распространяться и при отсутствии среды, т.е. в вакууме, со скоростью света с= 3×108 м/с. При движении в среде с постоянными значениями проницаемостей e и m скорость распространения электромагнитной волны меньше скорости света:
 ,
,
где  - показатель преломления среды.
- показатель преломления среды.
Для большинства прозрачных сред m = 1, отсюда  .
.
Показатель преломления n называется оптической плотностью среды.
ГЛАВА 7. Движение заряженных частиц в электрическом и магнитном полях
7.1. Движение заряженных частиц в однородном постоянном электрическом поле
7.2. Движение заряженных частиц в однородном постоянном магнитном поле
7.3. Движение заряженных частиц в однородных постоянных электрическом и магнитном полях
7.1. Движение заряженных частиц в однородном постоянном электрическом поле
В электрическом поле на заряженную частицу действует сила:
 , (7.1)
, (7.1)
где q – заряд частицы;
E – напряженность электрического поля.
Согласно второму закону Ньютона,  , тогда уравнение (7.1.) запишем в виде:
, тогда уравнение (7.1.) запишем в виде:
 . (7.2)
. (7.2)
Поскольку  то уравнение (7.2) можно записать в виде:
то уравнение (7.2) можно записать в виде:
 .
.
Отсюда находим:
 . (7.3)
. (7.3)
В скалярной форме получим уравнения для скоростей  :
:
 (7.4)
(7.4)
После интегрирования по t получим уравнения для координат:

 (7.5)
(7.5)
 .
.
Пример 1. Пусть начальная скорость  направлена вдоль силовых линий электрического поля
направлена вдоль силовых линий электрического поля  , тогда систему уравнений (7.4) запишем в виде:
, тогда систему уравнений (7.4) запишем в виде:
 (7.6)
(7.6)
Частица движется с ускорением вдоль оси x. Решение уравнений (6.33):

где w - циклическая частота волны;
 - волновое число;
- волновое число;
 - фазовая скорость волны;
- фазовая скорость волны;
 - скорость электромагнитной волны в вакууме;
- скорость электромагнитной волны в вакууме;
 - начальная фаза колебаний;
- начальная фаза колебаний;
 ,
,  - амплитуды переменных электрического и магнитного полей.
- амплитуды переменных электрического и магнитного полей.
Проинтегрируем уравнения (7.6) по времени и найдем координаты частицы в любой момент времени:

где  - начальная координата частицы.
- начальная координата частицы.
Пройдя разность потенциалов U в однородном поле, частица приобретает кинетическую энергию:
 .
.
Пример 2. Пусть теперь частица влетает в электрическое поле с напряженностью  в плоскости Oxy, под углом a к оси x, (рис. 7.1), тогда систему (7.5) запишем в виде:
в плоскости Oxy, под углом a к оси x, (рис. 7.1), тогда систему (7.5) запишем в виде:
 (7.7)
(7.7)
После интегрирования по времени находим координаты частицы в любой момент времени:
 (7.8)
(7.8)
Пусть  . Найдем зависимость x(y), для этого исключим время из уравнений (7.8):
. Найдем зависимость x(y), для этого исключим время из уравнений (7.8):
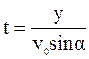 . (7.9)
. (7.9)
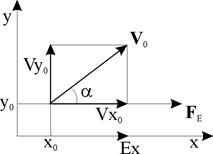
Рис. 7.1.
Получим уравнение вида 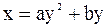 . На рис. 7.2 приведена траектория частицы:
. На рис. 7.2 приведена траектория частицы:

Рис. 7.2.
Частица одновременно движется ускоренно вдоль оси x и с постоянной скоростью  =
=  sina вдоль оси y.
sina вдоль оси y.
7.2. Движение заряженных частиц в однородном постоянном магнитном поле
В магнитном поле на заряженную частицу, движущуюся со скоростью 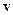 , действует сила Лоренца:
, действует сила Лоренца:
 , (7.10)
, (7.10)
где B - магнитная индукция.
Сила Лоренца направлена перпендикулярно к скорости движения частицы и к направлению вектора магнитной индукции, следовательно, она лежит в плоскости векторов v и B.
Направление силы Лоренца определяется по правилу левой руки (так же, как и силы Ампера):
Направим указательный палец по направлению магнитной индукции B, а средний палец вдоль вектора скорости положительно заряженных частиц v, тогда отогнутый большой палец покажет направление силы Лоренца.
Если  , то
, то 
 , следовательно, на покоящуюся частицу магнитное поле не действует.
, следовательно, на покоящуюся частицу магнитное поле не действует.
Найдем траектории заряженных частиц в магнитном поле в следующих случаях:
Пример 3. Пусть заряженная частица влетает в однородное магнитное поле вдоль силовых линий, тогда  , отсюда следует
, отсюда следует  . Частица будет двигаться с постоянной скоростью
. Частица будет двигаться с постоянной скоростью  вдоль силовых линий магнитного поля.
вдоль силовых линий магнитного поля.
Пример 4. Положительно заряженная частица влетает в магнитное поле перпендикулярно его силовым линиям. Сила Лоренца направлена перпендикулярно к вектору скорости, поэтому она не может изменить величину, а изменяет только направление скорости. Сила Лоренца представляет собой центростремительную силу  .
.
Частица будет двигаться по окружности радиуса R:
 . (7.11)
. (7.11)
Период обращения:
 , (7.12)
, (7.12)
не зависит от скорости частицы.
Пример 5. Скорость заряженной частицы направлена под острым углом к вектору магнитной индукции. Представим вектор v в виде суммы векторов v || и v ^:
 .
.
Компонента скорости v ||, параллельная силовым линиям магнитного поля, не изменяется, а скорость v ^ будет изменять направление. Частица будет двигаться поступательно вдоль силовых линий магнитной индукции и совершать вращательное движение в перпендикулярной плоскости. Траектория заряженной частицы представляет собой винтовую линию с шагом:
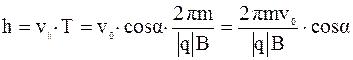 .
.
7.3. Движение заряженных частиц в постоянных однородных электрическом и магнитном полях
Действие электрического и магнитного полей на заряженную частицу характеризуется силой:
 . (7.13)
. (7.13)
Из выражения (7.13) следует, что напряженность электрического поля и магнитная индукция являются силовыми характеристиками полей.
Рассмотрим характер движения частиц в электрическом и магнитном полях.
Пример 6. Пусть вектора E и B сонаправлены. Заряженная частица влетает в область полей вдоль силовых линий. Проекцию уравнения (7.13) на направление силовых линий:  . Частица будет ускоренно двигаться вдоль силовых линий электрического и магнитного полей.
. Частица будет ускоренно двигаться вдоль силовых линий электрического и магнитного полей.
Пример 7. Вектора E и B взаимно перпендикулярны. Заряженная частица влетает со скоростью v перпендикулярно к силовым линиям однородных электрического и магнитного полей. Начальные координаты x0 = y0 = z0 =0. Начальные скорости:  . Пусть для определенности магнитная индукция направлена вдоль оси z, а напряженность электрического поля вдоль оси у. Уравнения движения частицы:
. Пусть для определенности магнитная индукция направлена вдоль оси z, а напряженность электрического поля вдоль оси у. Уравнения движения частицы:
 (7.14)
(7.14)
Продифференцируем первое уравнение системы (7.14) по времени и подставим 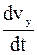 из второго уравнения:
из второго уравнения:
 .
.
Найдем скорости частицы вдоль осей x и y:

 ),
),
 ,
,
где  .
.
В начальный момент времени vx = vx0, vy = 0, отсюда находим:  , C = 0. Компоненты скорости частицы в момент времени t:
, C = 0. Компоненты скорости частицы в момент времени t:
 ,
,
 .
.
После интегрирования, при условии x0 = y0 = z0 = 0, получим уравнения:
 ,
,
 .
.
Кривая называется трохоидой. Частица совершает периодическое движение и дрейфует вдоль оси x со скоростью дрейфа:
 .
.
Полученный результат справедлив только в нерелятивистском случае, когда скорость частицы  , следовательно, при условии
, следовательно, при условии  .
.
Если силы F E и F Л, действующие на частицу сонаправлены, то ускорение равно
 ,
,  .
.
Ускорение частицы в случае противоположного направления сил F E и F Л:
 ,
,  .
.
Контрольные вопросы:
1. Уравнения Максвелла для постоянных электрических и магнитных полей в дифференциальной и интегральной формах.
2. Материальные уравнения. Уравнение непрерывности.
3. Полная система уравнений Максвелла для электромагнитного поля в дифференциальной и интегральной формах.
4. Плоская электромагнитная волна.
5. Связь между оптическими явлениями и теорией электромагнитного поля.
6. Сила Лоренца.
7. Правило правой руки.
8. Траектории заряженных частиц в электрических
и магнитных полях.
ГЛАВА 8. Интерференция света
8.1. Монохроматичность и когерентность волн
8.2. Интерференция света от двух когерентных источников. Опыт Юнга
8.3. Многолучевая интерференция
8.4. Интерференция света в тонких пленках
8.5. Кольца Ньютона
8.1. Монохроматичность и когерентность волн
Монохроматическими называются волны одинаковой частоты и постоянной амплитуды. Атомы источника света испускают волны определенной частоты в течение времени t  10-8с, затем излучение прекращается. Отдельный импульс излучения называется цугом волн. В следующий момент времени снова испускается цуг волн, но уже с другой частотой. Поскольку колебания электрона в атоме затухают в процессе излучения цуга волн, то амплитуда волн не является постоянной. Понятие монохроматической волны является идеализацией, так как атом излучает немонохроматические волны, кроме того, источник света состоит из большого числа независимо излучающих атомов.
10-8с, затем излучение прекращается. Отдельный импульс излучения называется цугом волн. В следующий момент времени снова испускается цуг волн, но уже с другой частотой. Поскольку колебания электрона в атоме затухают в процессе излучения цуга волн, то амплитуда волн не является постоянной. Понятие монохроматической волны является идеализацией, так как атом излучает немонохроматические волны, кроме того, источник света состоит из большого числа независимо излучающих атомов.
Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов.
Когерентными называются волны одинаковой частоты и постоянной разности фаз.
 (8.1)
(8.1)
Две монохроматические волны, распространяющиеся вдоль одного направления можно считать когерентными.
Для когерентности существуют временные и пространственные границы. Это связано с тем, что реальный источник нельзя рассматривать как точечный, испускающий монохроматические волны. Источник света испускает волны, частота которых лежит в диапазоне  . Изменение разности фаз на 2p, связанное с изменением частоты на Dw, происходит за время tког
. Изменение разности фаз на 2p, связанное с изменением частоты на Dw, происходит за время tког 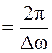 , называемое временем когерентности. За это время волна с частотой w и фазовой скоростью
, называемое временем когерентности. За это время волна с частотой w и фазовой скоростью  распространяется на расстояние lког, которое называется длиной когерентности:
распространяется на расстояние lког, которое называется длиной когерентности:
 . (8.2)
. (8.2)
Чем меньше ширина спектра частот  , тем ближе волна к монохроматической и тем больше время и длина ее когерентности.
, тем ближе волна к монохроматической и тем больше время и длина ее когерентности.
Для видимого света  Гц,
Гц,  ,
, 
Высокой степени когерентным может считаться вынужденное излучение лазеров, для которых время и длина когерентности:
tког = 10-5с, lког = 103 м.
Свет, испускаемый неточечным источником, является некогерентным, т.к. начальные фазы волн, из которых складывается излучение, изменяются хаотично, кроме того, частота этих волн различна.
Рассмотрим наложение двух колебаний, возбуждаемых в некоторой точке пространства:  и
и 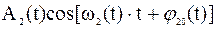 .
.
Пусть A1 = A2 = const. Интенсивность колебаний в данной точке I ~ A2, где  , отсюда следует:
, отсюда следует:
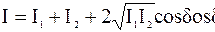 , (8.3)
, (8.3)
где  - разность фаз колебаний.
- разность фаз колебаний.
Прибор, регистрирующий интенсивность, имеет время срабатывания tприб. Если разность фаз d(t) быстро изменяется за время tприб, то прибор обнаружит интенсивность I = I1 + I2, т.к. среднее значение cos d(t) = 0.
Если разность фаз двух колебаний постоянна, то прибор обнаружит зависимость интенсивности результирующего колебания от разности фаз:
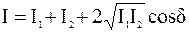 . (8.4)
. (8.4)
Интерференцией называется явление перераспределения интенсивности колебаний в данной точке, в зависимости от разности фаз колебаний.
Результат интерференции волн зависит от длины волны света l и оптической разности хода волн D от двух когерентных источников.
Необходимым условием наблюдения интерференции является когерентность двух волн. Для получения интерференционной картины необходимо, чтобы оптическая разность хода волн D была меньше, чем длина когерентности lког, т.е. волны должны принадлежать к одному акту испускания.
8.2. Интерференция света от двух когерентных источников. Опыт Юнга
Когерентные световые волны можно получить, если каким либо способом разделить волну, испускаемую одним источником на две или несколько волн, а затем соединить их (рис. 8.1).
Связь разности фаз d с оптической разностью хода
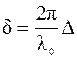 . (8.5)
. (8.5)
Условие интерференционного максимума:
 ,
,  , (m = 0,1,2,…). (8.6)
, (m = 0,1,2,…). (8.6)
Условие интерференционного минимума:
 ,
,  , (m = 0,1,2,…). (8.7)
, (m = 0,1,2,…). (8.7)

Рис. 8.1.
Поиск по сайту: