 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МОДЕЛИРОВАНИЕ ВНЕЗАПНЫХ ОТКАЗОВ
Построим интегральную функцию экспоненциального распределения:
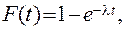
где l — интенсивность отказов.
Интенсивность отказов рассчитывается по формуле:
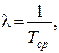
где Тср — среднее время наработки на отказ.
Примем среднюю наработку на отказ устройства при срезе валика (Х1) Тср = 20000 час;
F(4000)=0,18 F(24000)=0,7
F(8000)=0,33 F(32000)=0,8
F(14000)=0,5 F(48000)=0,9
F(20000)=0,63 F(800000)=0,98
По расчетным данным построим интегральную функцию экспоненциального распределения. На оси абсцисс отложим время t в 3¸4 раза больше Тср. На оси ординат — значение функции F (t).
На основе метода «Монте-Карло» промоделируем вероятность случайных отказов. Выбрасываем с помощью генератора случайных чисел числовую последовательность R в диапазоне значений (0¸1).

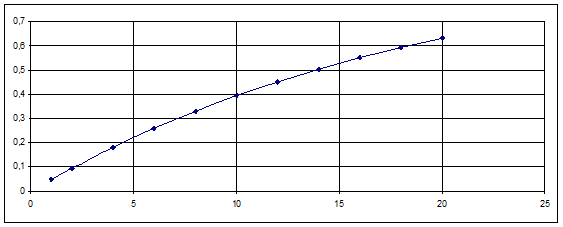
Интегральная функция экспоненциального распределения,
l=5´10-5, 1/час.
Временная выборка из пяти реализаций для шести элементов (X1) t ´103 час
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,5828 | |||||||||
| 0,525 | ||||||||||
| 0,609 | ||||||||||
| 0,565 | ||||||||||
| 0,4869 | ||||||||||
| Итого: 2,769 |
RX1= 0,554
 |
Далее временные значения ti, приведенные в таблице, сравниваем с Тср /2, поскольку нас интересует поведение системы в первый полупериод эксплуатации. Затем получим время t 0 нерабочего состояния элемента системы Х1, выбирая лишь те случаи, когда ti < Тср /2. Расчет производится по формуле

Полученное значение t 0 заносим в таблицу, указав его в скобках, затем суммируем нерабочее время в единичной реализации t 0 и берем отношение к сумме общего времени tобщ работы элемента в этой реализации. На основе полученных значений определим вероятность отказа элемента системы Х1 для данной реализации по формуле:

и так для каждой реализации.
Вероятность отказа элемента системы Х1 является средним арифметическим этих значений:
RX=1/5ΣRi,
RX1=0,554
Аналогично определяем вероятности отказов элементов системы RX2, Rx3, Rx4.
Примем среднюю наработку на отказ устройства Тср = 80 000 час;
F(12000)=0,26 F(48000)=0,7
F(16000)=0,33 F(80000)=0,865
F(28000)=0,5 F(92000)=0,9
F(36000)=0,6 F(196000)=0,99
 |
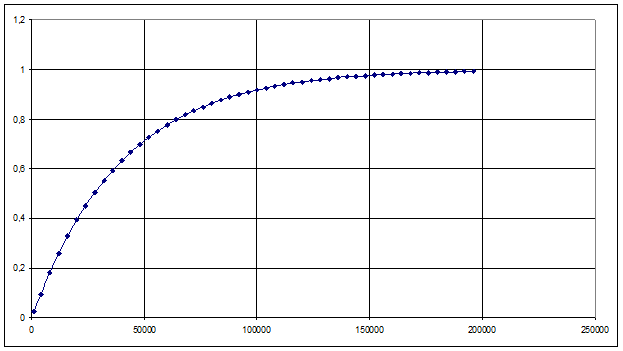
Интегральная функция экспоненциального распределения,
l=2,5´10-5, 1/час.
 Временная выборка из пяти реализаций для шести элементов (X2) t ´103 час
Временная выборка из пяти реализаций для шести элементов (X2) t ´103 час
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,333137 | |||||||||
| -15155 | ||||||||||
| 0,541155 | ||||||||||
| 0,559676 | ||||||||||
| 0,5695 | ||||||||||
| 0,480027 | ||||||||||
| Итого: 2,483 |
RX2=0,497
Временная выборка из пяти реализаций для шести элементов (Х3) t ´103 час
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,201993 | |||||||||
| 0,621473 | ||||||||||
| 0,295705 | ||||||||||
| 0,32163 | ||||||||||
| 0,21783 | ||||||||||
| Итого:1,6586 |
RX3=0,332
Временная выборка из пяти реализаций для шести элементов (Х4) t ´103 час
| m n | Количество элементов | S t 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,049345 | |||||||||
| -8742 | ||||||||||
| 0,3013 | ||||||||||
| 0,41087 | ||||||||||
| 0,287638 | ||||||||||
| 0,248673 | ||||||||||
| Итого: 1,2978 |
RX4=0,26

Поиск по сайту: