 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МОДЕЛИРОВАНИЕ ПОСТЕПЕННЫХ ОТКАЗОВ
Постепенные отказы подчиняются нормальному закону распределения. Интегральная функция нормального закона имеет вид:
где d — среднеквадратичное отклонение;
a — математическое ожидание.
Для того чтобы не рассчитывать интеграл, воспользуемся половинной функцией Лапласа и с ее помощью рассчитаем нормальный закон распределения по формуле:
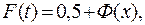
где Ф (х) — половинная функция Лапласа;
х =(t - Tср)/d, где
х — аргумент функции Лапласа;
t — время функционирования;
Тср — средняя наработка на отказ;
d — среднеквадратичное отклонение.
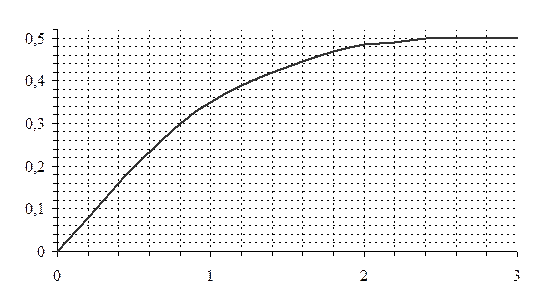
На рисунке представлен график половинной функции Лапласа.
 |
Рассчитаем интегральную функцию F (t) нормального распределения для Х1, задавшись Тср = 80000 час., d=500, определим аргумент функции Лапласа и занесем данные в таблицу.
Сводная таблица расчета интегральной функции
нормального распределения (Х1)
| t´104, час. | 6,5 | 7,5 | 8,5 | 9,5 | |||||
| Х | -4 | -3 | -2 | -1 | |||||
| Ф(х) | -0,5 | -0,5 | -0,48 | -0,34 | 0,34 | 0, 48 | 0,5 | 0,5 | |
| F(t) | 0,02 | 0,16 | 0,5 | 0,84 | 0,98 |
На основе расчетных данных построим график нормального распределения.
Полученную выборку 6´5 заносим в таблицу.
Полученные в таблице значения сравниваем с Тср, т. к. нас интересуют характеристики системы в первый период эксплуатации. В тех случаях, если t 0< Tср, находим нерабочее время t 0 элемента системы Х1 по формуле 
. Полученное время указано в скобках в таблице. Затем, просуммировав время t 0 по реализации, берем отношение t 0 к суммарному времени функционирования элемента системы Х5 в этой реализации 
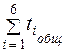. Вероятность отказа элемента системы Х5 в данной реализации определяем по формуле:
 |
| m n | Количество элементов | Σt 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,37232 | |||||||||
| 0,4373 | ||||||||||
| 0,48296 | ||||||||||
| -2 | ||||||||||
| 0,33227 | ||||||||||
| 0,2901 | ||||||||||
| Итого: 1,915 |
Полный коэффициент отказа системы RX1 рассчитывается как
RX5=1/5ΣRi,
RX5= 1,915/5=0,383
Аналогично промоделируем для остальных элементов Х6, Х7, Х8, Х9, Х10. Эти элементы системы имеют тоже самое время наработки на отказ, необходимо повторить процесс моделирования по графику.
 |
Временная выборка из 6х5 элементов (Х6).
| m n | Количество элементов | Σt 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,23419 | |||||||||
| 0,58578 | ||||||||||
| 0,5466 | ||||||||||
| 0,6768 | ||||||||||
| 0,4618 | ||||||||||
| Итого: 2,505 |
RX6=0,501
Временная выборка из 6х5 элементов (Х7).
| m n | Количество элементов | Σt 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,64312 | |||||||||
| 0,78007 | ||||||||||
| 0,33688 | ||||||||||
| 0,46261 | ||||||||||
| 0,5134 | ||||||||||
| Итого: 2,736 |
RX7=0,547
 |
Временная выборка из 6х5 элементов (Х8).
| m n | Количество элементов | Σt 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,54863 | |||||||||
| 0,61155 | ||||||||||
| 0,39376 | ||||||||||
| 0,34994 | ||||||||||
| 0,43222 | ||||||||||
| Итого: 2,336 |
RX8=0,467
 |
Временная выборка из 6х5 элементов (Х9).
| m n | Количество элементов | Σt 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,470063 | |||||||||
| 0,484683 | ||||||||||
| 0,239198 | ||||||||||
| 0,458069 | ||||||||||
| 0,422876 | ||||||||||
| Итого: 2,075 |
RX9=0,415
Временная выборка из 6х5 элементов (Х10).
| m n | Количество элементов | Σt 0 | S tобщ | S t 0/S tобщ | ||||||
| Количество реализаций | 0,445789 | |||||||||
| 0,527041 | ||||||||||
| 0,303196 | ||||||||||
| 0,447158 | ||||||||||
| 0,455696 | ||||||||||
| Итого: 2,17888 |
RX10=0,436
Вероятности отказа элементов системы:
RX1=0,554 RX6 = 0,501
RX2=0,497 RX7 = 0,547
RX3=0,332 RX8 =0,467
RX4=0,26 RX9= 0,415
RX5 = 0,383 RX10 = 0,436
В результате процедуры моделирования получим коэффициенты отказов каждого элемента системы. Рассчитаем коэффициент отказа всей системы, используя формулы для последовательного и параллельного соединения.
для «ИЛИ» 
для «И» 
Рассчитаем коэффициент отказа системы
RА = RХ7∙RХ 
8=0,255
RВ = RХ9∙RХ 10=0,181
RС = RХ5∙RХ 
6=0,192
Рассчитаем коэффициент отказа системы RКС по формуле:
RКС = 1- (1 – RХ2) ∙ (1 – RХ3) ∙ (1 – RХ4) ∙ (1 - RА) ∙ (1 – RХ1) ∙ (1 – RВ) ∙ (1 - - RС)
RКС =0,945
Вывод: данное устройство рассчитано на работу с вероятностью отказа 0,945.
Поиск по сайту: