АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Реальные газы. Уравнение Ван-дер-Ваальса

Читайте также:
  1. V2: Волны. Уравнение волны
  2. V2: Уравнение Шредингера
  3. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  4. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  5. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  6. В простом случае обычное дифференциальное уравнение имеет вид
  7. Взаимосвязь мероприятий по охране труда и рентабельности работы хозяйственных субъектов. Реальные способы улучшения условий труда и его охраны без конфликтов с работодателями.
  8. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  9. Волна вероятности. Уравнение Шредингера
  10. Волновая функция.Уравнение Шредингера
  11. Волновое уравнение для упругих волн и его общее решение.
  12. Волновое уравнение для электромагнитных волн

Поведение реальных газов хорошо удовлетворяет модели идеального газа при уравнении Менделеева-Клапейрона только при малых плотностях. Малые плотности газа реализуются только при малых давлениях и высоких температурах. С ростом давления при постоянной температуре левая часть уравнения должна оставаться постоянной, однако при давлениях порядка в 100 атмосфер наблюдается заметное отклонение от равенства. Для описания поведения газа в широком интервале давлений и температур записывается уравнение Ван-дер-Ваальса:

где

· — давление,

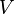· — молярный объём,

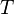· — абсолютная температура,

· — универсальная газовая постоянная.

Коэффициенты a и b - есть константы Ван-дер-Ваальса, имеющие разные значения для различных газов.

Анализ формулы показывает, что - есть добавка к внешнему давлению, которое обусловлено взаимным притяжением молекул друг к другу. Их взаимодействие существенно на небольших расстояниях, определяемых R молекулярного действия. = .

Коэффициент «b» определяет объём молекул в сосуде.

Внутренняя энергия 1 моля газа: U = T +

Уравнение Ван-дер-Ваальса представляет собой уравнение третьей степени относительно объёма. Это уравнение имеет три вещественных корня.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)