 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Симплексные таблицы
Признак оптимальности опорного плана. Задача максимизации
Если для некоторого опорного плана все оценки dj неотрицательны, то такой план оптимален. Если же исходная задача на минимум и dj не положительны, то такой план оптимален.
Рассмотрим переход к нихудшему опорному плану на примере задачи ЛП на макс.
Если в индексной строке dj < 0, то план не оптимален и его можно улучшить. Среди отрицательных оценок находят максимальную по абсолютной величине.
Max|dj|=|dj0|
Если задача на минимум, то разрешающий столбец Max|dj|=|dj0|
Переменную Xj0, следует ввести в базис. Для определения переменной, выводимой из базиса, находят отношения: Bi/Aij, Aij >0
Min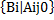 
= Bi0/Ai0j0
НА пересечении разрешающей строки и разреш столбца находиться разр элемент.
1.Элементы строки I0 новой таблицы равны соответствующим элементам разрешающей строки предыдущей таблицы деленной на разреш элемент.
2.Все элементы столбцы J0 равны 0, за исключением разрешающего элемента.
3.Все остальные элементы новой таблицы высчитываются по правилу: произведение главной диагонали минус произведение побочной диагонали деленной на разрешающий элемент.
Три признака:
1.Альтернативный оптимум (признак бесконечности множества оптимальных планов). Если в индексной строке последней симплексной таблицы (содержащей оптимальный план) имеется хотя бы одна нулевая оценка, соответствующая свободной переменной, то задача ЛП имеет бесконечное множество оптимальных планов.
2.Признак неограниченности целевой функции. Если в разрешающем столбце нет ни одного положительного элемента, то целевая функция на множестве допустимых планов не ограничена.
3.Признак несовместности системы ограничений. Если в оптимальном плане М-задачи не все искусственные переменные равны 0, то система ограничений исходной задачи несовместна.
Пример:
MaxZ = 5X1+7X2+6X3+9X4+8X5
0,7X1+0,9X2+1,3X3+2,3X4+1,8X5<=50000|+ X6
1,4X1+0,3X2+0,7X3+2,5X4+2X5<=28000 |+ X7
0,5X1+2,1X2+1,8X3+0,7X4+2X5<=40000 |+ X8
| БП | СБ | А0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 |
| Х6 | 0,7 | 0,9 | 1,5 | 2,3 | 1,8 | |||||
| Х7 | 1,4 | 0,3 | 0,7 | 2,5 | ||||||
| Х8 | 0,5 | 0,5 | 1,8 | 0,7 | ||||||
| -5 | -7 | -6 | -9 | -8 | ||||||
| Х6 | -0,59 | 0,62 | 0,86 | 0,04 | 0,92 | |||||
| Х4 | 0,56 | 0,12 | 0,28 | 0,8 | 0,4 | |||||
| Х8 | 0,11 | 2,02 | 1,6 | 0,8 | 0,4 | |||||
| 0,04 | -5,92 | -3,48 | -0,8 | 3,6 | ||||||
| Х6 | -1,05 | |||||||||
| Х4 | 1,1168 | |||||||||
| Х2 | 0,05 | |||||||||
Оптим Х = (0,15952,0,9286,0,14286,0,0)
Желтый столбец – разрешающий
А0 - Вi
Bi/A0i – 28000/2,5 => Х4 заменит Х7
Начиная с А0 итое делим все на разреш элемент
(50000*2,5 – 2,3*2800)/2,5 =
Пример:
Zmax = 9X1+6X2-3X3+0X4-0X5-0X6 – M(W1+W2)
-X1+X2+X3=4|
X2+X1<=10 | +X4
3X1+X2>=9 | -X5+W1
-X1+3X2>=3 | -X6+W2
| БП | СБ | А0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | W1 | W2 |
| -3 | -M | -M | ||||||||
| X3 | -3 | -1 | ||||||||
| X4 | ||||||||||
| W1 | -M | -1 | ||||||||
| W2 | -M | -1 | -1 | |||||||
| -12-12M | -6- 2M | -9-4M | M | M | ||||||
| БП | СБ | А0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | W1 | W2 |
| -3 | -M | -M | ||||||||
| X3 | -3 | -2/3 | 1/3 | -1/3 | ||||||
| X4 | 4/3 | 1/3 | -1/3 | |||||||
| W1 | -M | 10/3 | -1 | 1/3 | -1/3 | |||||
| X2 | -1/3 | -1/3 | 1/3 | |||||||
| -3-8M | -10M/3 | M | -3-m/3 | 3+4M/3 | ||||||
| БП | СБ | А0 | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | W1 | W2 |
| -3 | -M | -M | ||||||||
| X3 | -3 | 4,6 | -0,2 | 12/30 | 0,2 | -8/30 | ||||
| X4 | 5,8 | 0,4 | 6/30 | 0,4 | -6/30 | |||||
| X1 | 2,4 | -0,3 | 0,1 | 0,3 | -0,1 | |||||
| X2 | 1,8 | -0,1 | -9/30 | 0,1 | 9/30 | |||||
| 18,6 |
С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Первоначальная задача – прямая или исходная. Пара симметричных двойственных задач ЛП имеет следующий вид:
Прямая - maxZ = 
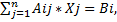Xj>=0
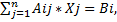minZ = Xj>=0
Пара двойственных задач может быть экономически интерпретирована:
Примая – Сколько и какой продукции Xj надо произвести чтобы при заданных стоимостях единицы продукции Cj объемах ресурсов Bi и нормах расхода Aij максимизироваит выпуск продукции в стоимостном выражениии.
Двойственная – Какова должна быть оценка единицы каждого из ресурсов чтобы при заданных Bi Cj Aij минимизировать общую оценку затрат на все ресурсы.
Правила построения:
1.Упорядочивается запись исходной задачи, т.е. если целевая функция задачи максимизируется, то ограничения неравенства должны быть > или =(для минимиз < или =) Достигается умножением ограничений на -1.
2.Если прямая задача решается на максимум, то двойственная на минимум.
3.Каждому ограничению прямой задачи соответствует переменная двойственной задачи и наоборот.
4.Матрица системы ограничений двойственной задачи получается из матрицы системы ограничений прямой задачи путем транспонирования.
5.Свабодные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции прямой задачи и наоборот.
6.Если на перенесение прямой задачи наложено условие не отрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение неравенства, если де нет – как ограничение равенства.
7.Если какое-либо ограничение прямой задачи записывается как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.
Пример
-12X1+10 X2 -15 X3 -11 X4 =maxZ
2X1-4 X2 +4 X4 >=3 |домножим на -1
X1+ X2 +2 X3 +2 X4 =4 |-1
…
-2X1+4 X2 -4 X4 <=-3 |y1
X1+ X2 +2 X3 +2 X4 =4 |y2
Далее транспонируем матрицу исходной задачи
-2 y1 + 1 y2 >=(из исходной функции максимизации)-12
4 y1 +1 y2=10
0 y1 +2 y2=-15
-4 y1 +2 y2>=-11
Если какой либо y* >0, те ресурсы используются полностью, равны 0 – избыточные.
Поиск по сайту: