Поперечное сечение, плоское до деформации, остается плоским и после деформации (гипотеза плоских сечений Бернулли)

1.4. Определение внутренних усилий. Метод мысленных сечений

Итак, в сопротивлении материалов не учитывается реальная атомная структура материала твердого тела. Исходя из этого, сплошность и однородность тела обеспечивается не межатомными силами, а гипотетическими внутренними усилиями.

Внутренние усилия – силы взаимодействия (сцепления) между частицами тела, возникающие внутри элемента конструкции, как противодействие внешнему нагружению.

Внутренние усилия во всех случаях стремятся сохранить тело как единое целое, противодействуя всякой попытке изменить взаимное расположение частиц, т. е. деформировать и разрушить тело. Поэтому именно величиной внутренних усилий определяется возможность разрушения в том или ином опасном сечении элемента конструкции. Таким образом, для решения задач сопротивления материалов необходимо уметь выявлять, а затем определять величину и направление внутренних усилий. При их нахождении широко используется метод мысленных сечений.

Выполнение гипотезы сплошности твердого деформируемого тела обеспечивается внутренними связя ми, природа которых не рассматривается в сопротивлении материалов. Разрезая тело какой-либо плоскостью, мы мысленно разрушаем эти связи, но для равновесия системы заменяем нарушенные связи силами, которые называются внутренними. Для их определения следует рассмотреть равновесие любой части тела по одну сторону от плоскости мысленного сечения.

Необходимо подчеркнуть, что из уравнений равновесия для оставленной части тела определяется не закон распределения внутренних сил, а их статический эквивалент в выбранной точке приведения, то есть главный вектор с проекциями N, Q_y, Q_z и главный момент с проекциями M_x, M_y, M _z. В сопротивлении материалов эти проекции часто называют внутренними усилиями.

Метод мысленных сечений позволяет отбросить ненужный для расчета элемент конструкции (или часть этого элемента), заменить его силой, действие которой будет эквивалентно действию отброшенного элемента (его части).

Если задача статически определима, то для определения этой силы достаточно использовать уравнения равновесия (уравнения статики).

Рассмотрим какой-либо элемент (например, брус), находящийся в равновесии под действием внешних сил. Пусть требуется определить внутренние усилия в произвольном сечении бруса.

Применим для этого метод мысленных сечений:

а) мысленно рассечем элемент плоскостью А – А;

б) отбросим ненужную (наиболее сложно нагруженную) часть элемента, действие отброшенной части заменим внутренними усилиями;

в) внутренние усилия приведем к главному вектору R и главному моменту M, главный вектор и главный момент разложим по трем взаимно перпендикулярным осям x, y и z (ось x – нормальна к сечению элемента);

г) внутренние усилия (N, Q_y, Q_z, M_x, M_y, M_z) определим из уравнений равновесия оставшейся части элемента

N – осевое (продольное) усилие. Осевое усилие равно сумме проекций на ось x всех внешних сил, действующих с одной стороны сечения:

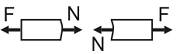Осевое усилие вызывает растяжение (сжатие) элемента.

Q_y, Q_z – поперечные силы. Поперечные силы равны сумме проекций всех внешних сил (с одной стороны сечения) на оси y и z соответственно:

Поперечные силы вызывают сдвиг в сечении элемента.

M_x – крутящий момент (T, M_кр). Крутящий момент равен сумме моментов внешних сил (с одной стороны сечения) относительно оси x:

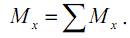
Крутящий момент вызывает кручение элемента.

M_y, M_z – изгибающие моменты. Изгибающие моменты равны сумме моментов внешних сил относительно осей y и z соответственно:

Изгибающие моменты вызывают изгиб элемента.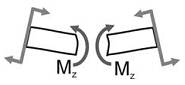

Таким образом, введя понятие внутренних усилий, мы получили возможность свести все многообразие внешних нагрузок и конфигураций элементов к 6-ти силовым факторам (N, Q_y, Q_z, M_x, M_y, M_z) и представить даже самое сложное внешнее воздействие как сочетание 4-х видов нагружения: растяжения, сдвига, кручения, изгиба.

Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.

Сопротивления, при которых в поперечном сечении бруса дей­ствует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий сопротивление бруса называется сложным.

При выполнении практических рас­четов, для наглядности, как правило, определяются графики функ­ций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изме­нения внутренних усилий вдоль продольной оси стержня называ­ются эпюрами.

1.5. Понятие о нормальных и касательных напряжениях

Установить закон (характер) распределения внутренних усилий по сечению элемента методами статики не представляется возможным: составляя уравнения равновесия для сил, приложенных к отсеченной части элемента, можем найти лишь статический эквивалент внутренних усилий, возникающих в рассматриваемом сечении. Чтобы характеризовать закон распределения внутренних усилий по сечению элемента, необходимо ввести для них числовую меру. За такую меру принимается напряжение.

В сопротивлении материалов неявно предполагается, что внутренние усилия достаточно равномерно распределены на малой площадке в окрестности любой точки мысленного сечения. Поэтому отношение главного момента к величине площадки стремится к нулю вместе с этой площадкой. В результате

на данной площадке dA остается главный вектор сил dR, отношение которого

к величине площадки dA при стягивании последней в точку, называется полным напряжением p:

Напряжение – есть внутренняя сила, отнесенная к единице площади в данной точке рассматриваемого сечения (иначе говоря, интенсивность внутреннего усилия в данной точке сечения).

Размерность напряжения: Н/м², то есть Па (МПа, кПа)

В расчетах удобнее пользоваться не полным напряжением p, а его нормальной σ и касательными τ составляющими. Рассмотрим эти понятия.

Проекциями вектора dR на оси x, y, z будут элементарное осевое усилие dN и элементарные поперечные силы dQ_y, dQ_z. Разделив величины dN, dQ_y, dQ_z на бесконечно малую площадь dA, получим величины продольных и поперечных сил, приходящихся на единицу площади в данной точке сечения.

Нормальное напряжение (σ_x) – интенсивность осевого внутреннего усилия, или осевое усилие, приходящееся на единицу площади в данной точке рассматриваемого сечения

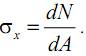
Касательное напряжение (τ_y, τ_z) – интенсивность внутренних поперечных сил, или поперечная сила, приходящаяся на единицу площади в данной точке рассматриваемого сечения

Таким образом, на площадке могут возникать два вида напряжений: нормальные и касательные. В соответствии с двумя видами напряжений на наиболее опасной площадке (там, где напряжения максимальны) может реализовываться два различных механизма разрушения – отрыв или срез.

Поиск по сайту: