Системы координат

В зависимости от решаемых задач и от размеров отображаемых участков земной поверхности используются различные системы координат. Основными критериями при их выборе служат точность и эффективность решения возникающих задач. Наиболее часто применяются сфероидические координаты, плоские и пространственные прямоугольные координаты, полярные координаты.

В системах сфероидических координат положение точки на эллипсоиде задается широтой и долготой. Широта и долгота определяются относительно экватора и начального меридиана. Меридианом называют сечение эллипсоида плоскостью, проходящей через малую ось эллипсоида, а соответствующую плоскость - плоскостью меридиана. Гринвичский меридиан принято считать начальным, или нулевым. Долготой точки на эллипсоиде называют двугранный угол между плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку (рис. 1.5). Долгота обычно обозначается латинской буквой L или греческой буквой λ и отсчитывается от Гринвичского меридиана от 0° до 180° на восток (восточная долгота) и на запад (западная долгота). Более удобным является отсчитывание долгот от Гринвичского меридиана на восток от 0° до 360°.

Сечения эллипсоида плоскостями, перпендикулярными малой оси, образуют окружности, называемые параллелями. Экватором называют сечение эллипсоида плоскостью, перпендикулярной малой оси и проходящей через центр эллипсоида. Таким образом, экватор – это параллель с наибольшим радиусом.

Геоцентрической широтой φ точки на эллипсоиде называют угол между радиус-вектором этой точки и плоскостью экватора (рис. 1.5). Геодезической широтой B точки на эллипсоиде называют угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора. Приведенной широтой u точки на эллипсоиде называют широту точки на сфере, являющейся прообразом точки на эллипсоиде при линейном отображении сферы на эллипсоид.

Геодезические координаты представляют собой три величины, две из которых характеризуют направление нормали к поверхности земного эллипсоида в данной точке пространства относительно экватора (геодезическая широта) и начального меридиана (долгота), а третья является высотой точки над поверхностью земного эллипсоида [ГОСТ 22268].

В системе прямоугольных пространственных геоцентрических координат XYZ начало координат совпадает с центром эллипсоида, ось Z направлена по малой полуоси от центра эллипсоида к северному полюсу, ось X совпадает с пересечением плоскости экватора и плоскости начального меридиана; ось Y лежит в пересечении плоскости экватора и плоскости меридиана с долготой 90° (рис. 1.6). Данная система координат используется преимущественно в космической геодезии.

Рис. 1.5. Долготы и широты

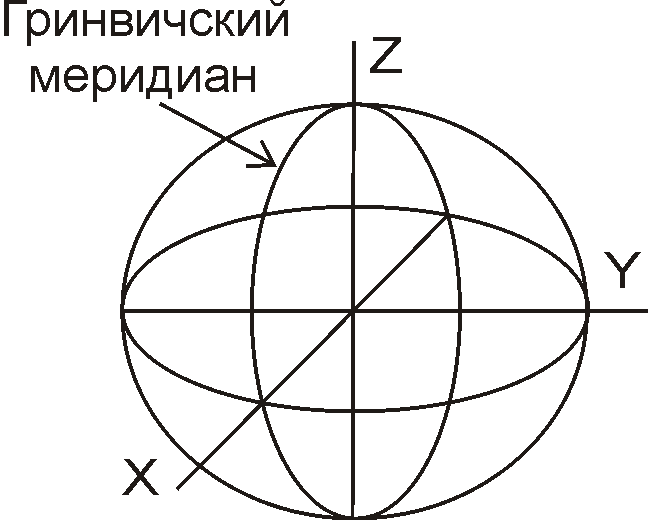Рис. 1.6. Система прямоугольных пространственных координат

Положение точки на плоскости может определяться в системе плоских прямоугольных координат и в системе полярных координат. Плоские прямоугольные геодезические координаты представляют собой прямоугольные координаты на плоскости, на которой отображена по определенному математическому закону поверхность земного эллипсоида [ГОСТ 22268]. В системе полярных координат на прямой, называемой полярной осью, выбирается точка, служащая полюсом, и на этой прямой задается направление, от которого отсчитываются углы по часовой стрелке. Положение точки определяется значением угла и значением расстояния от нее до полюса.

При съемках сравнительно небольших участков местности используются условные системы координат. Хотя такие координаты более удобны, так как они изменяются в небольших пределах, и оперировать ими проще, они обладают тем недостатком, что не дают возможности представить положение точки на земном эллипсоиде.

Проекция Гаусса – Крюгера. Для выполнения съемок в пределах всей территории России используются проекция Гаусса - Крюгера и общегосударственная система координат, введенная в действие в 1928 г.

Построение проекции Гаусса – Крюгера можно пояснить следующим образом (рис. 1.7). Вся поверхность земного эллипсоида, начиная с Гринвичского меридиана, разбивается на сферические двуугольники - зоны шириной 6° по широте. Далее каждая зона из центра эллипсоида проектируется на поверхность цилиндра, после чего цилиндр разрезается по образующей и разворачивается в плоскость. В результате получают картину, представленную на рис. 1.8. В такой проекции средний меридиан отображаемой зоны, называемый осевым меридианом, и дуга экватора изображаются отрезками прямых линий; остальные меридианы и параллели изображаются кривыми.

Счет зон ведется на восток от Гринвича от 1 до 60. В каждой зоне вводится система плоских прямоугольных координат (рис. 1.9), начало которой совпадает с точкой пересечения осевого меридиана и экватора. Долгота 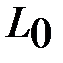осевого меридиана зоны связана с ее номером n соотношением

.

Ось X совпадает с изображением осевого меридиана, положительным направлением оси X считается направление на север, положительным направлением оси Y – направление на восток. Значение X в начале координат принимается равным 0. Значение Y в начале системы координат принимается равным выражению N 500 000 + у, где N - номер зоны, 500 000 м - значение, прибавляемое к y, чтобы избавиться от отрицательных значений ординат, y – расстояние от осевого меридиана до заданной точки. Пусть, например, заданная точка находится в 37 зоне, и ее ордината равна 123 456,78 м. Тогда запись ординаты в проекции Гаусса-Крюгера будет представлена значением 37 623 456,78 м.

Рис. 1.7. Проекция Гаусса - Крюгера

Рис. 1.8. Зоны в проекции Гаусса – Крюгера

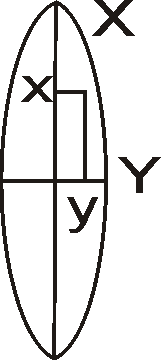Рис. 1.9. Система координат в проекции Гаусса - Крюгера

Значения координат зависят от ориентации эллипсоида внутри тела Земли. Такие работы были закончены в СССР в 1942 г, в связи с чем соответствующая система координат получила название Системы координат 1942 года (СК-42). В 1990-х годах было выполнено уточнение размеров и фигуры эллипсоида и его ориентации в теле Земли, и новая система координат получила название СК-95 (Система координат 1995 г). Различия между значениями координат в СК-42 и СК-95 возрастают с запада на восток и на северо-востоке России достигают 30 м.

Для представления положения точек в пределах всего земного шара в России принята система координат, называемая ПЗ-90 (Параметры Земли 1990 г).

Поиск по сайту: