Фигура Земли

Исходными понятиями при определении фигуры и размеров Земли служат понятия отвесной линии и уровенной поверхности. Отвесная линия есть прямая, совпадающая с направлением действия силы тяжести в данной точке [ГОСТ 22268]. Уровенной поверхностью называют поверхность, в каждой точке которой нормаль к поверхности совпадает с отвесной линией. Существует бесконечное множество уровенных поверхностей: через каждую точку околоземного пространства можно провести (единственную) уровенную поверхность. Уровенные поверхности всюду непрерывны, замкнуты и выпуклы (рис. 1.2). За фигуру Земли в целом принимается геоид - уровенная поверхность, совпадающая с поверхностью Мирового океана в состоянии полного покоя и равновесия и продолженная под материками [ГОСТ 22268].

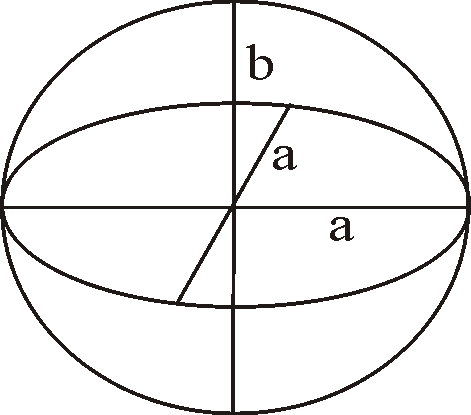
Рис. 1.2. Уровенные поверхности Рис. 1.3. Земной эллипсоид

Форма уровенных поверхностей зависит от распределения масс внутри Земли, центробежной силы, возникающей вследствие суточного вращения Земли, влияния Луны и планет солнечной системы и других менее значимых факторов, например, распределения воздушных масс в околоземном пространстве. Уравнение геоида является очень сложной функцией, которая не может быть определена без знания распределения плотностей масс внутри Земли. Поэтому по предложению советского геодезиста М. С. Молоденского изучение геоида заменяется изучением квазигеоида – поверхности, на океанах совпадающей с геоидом, а на материках отклоняющейся от него не более чем на 2 м.

Поверхность геоида является физической моделью Земли, она близка к поверхности сфероида, или эллипсоида вращения, полученного вращением эллипса вокруг малой оси. Поэтому в качестве геометрической модели земной поверхности принимают эллипсоид вращения. Отклонение геоида от эллипсоида не превышает 150 м. При этом различают земной эллипсоид и референц-эллипсоид. Под земным эллипсоидом понимается эллипсоид, характеризующий фигуру и размеры Земли в целом. Референц-эллипсоид – эллипсоид, принятый для обработки геодезических измерений и установления системы геодезических координат в пределах страны или группы стран.

В СССР (а теперь и в России) в качестве геометрической модели Земли был принят эллипсоид Красовского, большая полуось которого a = 6 378 245 м, малая полуось b = 6 356 863 м, сжатие a, называемое иногда полярным и представляющее собой отношение (рис. 1.3)

.

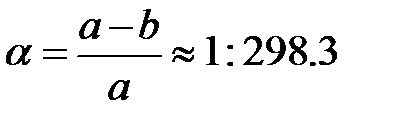Другими величинами, характеризующими форму эллипсоида, являются первый эксцентриситет

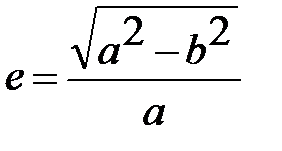
и второй эксцентриситет

.

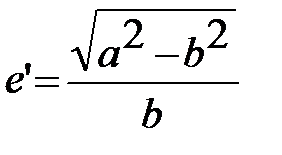В математике эксцентриситет e эллипса определяется как отношение расстояния любой точки эллипса до фокуса к расстоянию ее до соответствующей директрисы [МЭС]:

. (*)

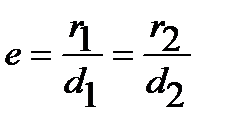Можно показать, что данное определение эксцентриситета e и “геодезическое” определение первого эксцентриситета являются эквивалентными. С этой целью запишем значение эксцентриситета эллипса для точки P (рис. 1.3.а):

, (**)

где δ – расстояние от точки экватора до директрисы 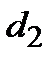. Значение эксцентриситета для точки 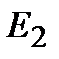на экваторе может быть представлено выражением

. (***)

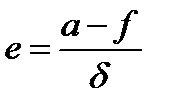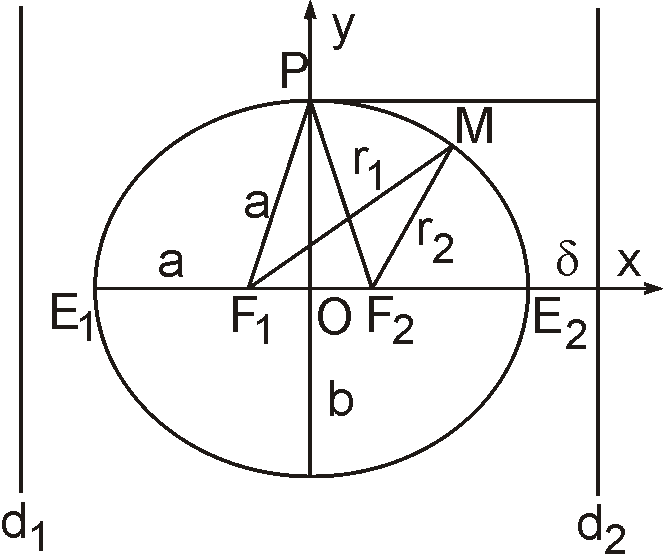
Рис. 1.3.а. Параметры эллипса

Из сравнения двух последних выражений следует

.

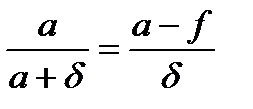Отсюда далее находим

.

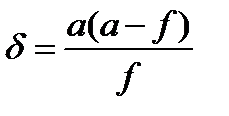Подставив данное значение в (**) или в (***), получаем

,

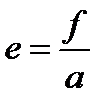а это и есть значение первого эксцентриситета. Таким образом, мы установили эквивалентность “математического” определения эксцентриситета и “геодезического” определения первого эксцентриситета. Преимущество формулы (*) в том, что значение эксцентриситета служит характеристикой не только эллипса, но и других конических сечений – параболы и гиперболы. Достоинство выражения для первого эксцентриситета состоит в очевидности, оно более наглядно выражает форму эллипса: чем больше разность полуосей a и b, тем больше эксцентриситет, и наоборот. При 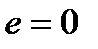эллипс превращается в окружность.

Можно дать другую интерпретацию первого и второго эксцентриситетов. На рис. 1.3.b точки F ₁ и F ₂ - фокусы эллипса, P - полюс, отрезок прямой PF ₁ равен большой полуоси. Легко видеть, что первый эксцентриситет

,

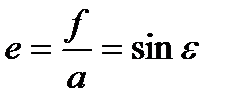второй эксцентриситет

,

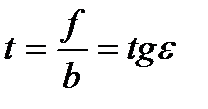где символ t использован для обозначения второго эксцентриситета как более удобный и как напоминание о тангенсе угла ε между отрезком PF ₁ и малой полуосью b.

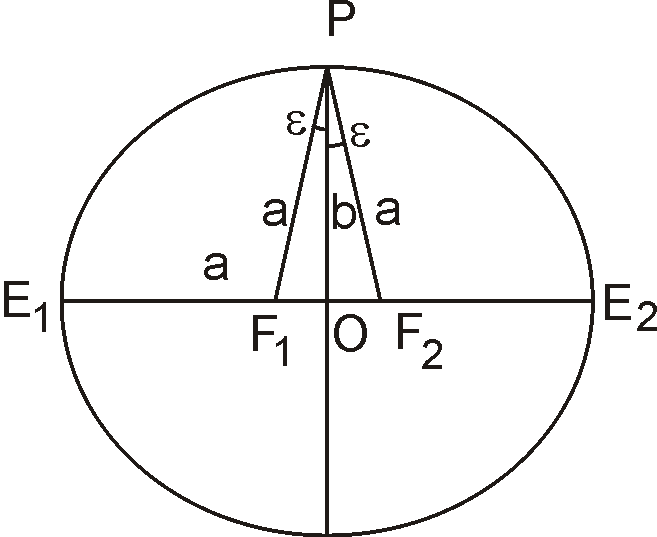
Рис. 1.3.b. К интерпретации

основных параметров эллипса.

Таким образом, основным (или первичным) параметром формы эллипса можно считать угол ε. Значения всех величин, характеризующих форму эллипса, легко могут быть получены как функции угла ε, в частности: 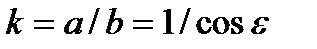и т.п.

Поиск по сайту: