Мощности конечных множеств

В комбинаторном анализе существует целый ряд подходов для изучения комбинаторных объектов и чисел.

Теоретико-множественный подход.

Данный подход связан с вычислением мощностей конечных множеств. Пусть – система подмножеств конечного множества. Спрашивается, как найти мощности множеств, образованных из множеств с помощью теоретико-множественных операций. Оказывается, что для этого надо знать только мощности самих множеств и их пересечений.

Теорема 5. (принцип включения-выключения)

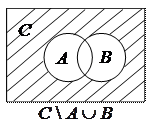Пусть А и В два произвольных подмножества множества С. Тогда для мощностей множеств справедливо соотношение:

. (2.4.1)

Следствие. Пусть А и В два конечных множества, тогда для мощности их объединения справедливо соотношение:

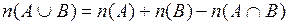. (2.4.2)

Доказательство:

Из формулы (14) в случае 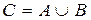находим

.

Что и требовалось доказать. ■

Формула (2.4.2) допускает обобщения на случай объединения любого конечного числа множеств. В частности, для трех множеств имеем:

Поиск по сайту: