АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод конечных разностей. Включает следующие этапы

Читайте также:
  1. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Методические основы
  4. I. Методические основы оценки эффективности инвестиционных проектов
  5. I. Предмет и метод теоретической экономики
  6. I. Что изучает экономика. Предмет и метод экономики.
  7. I. ЭТАПЫ ПРОТЕКАНИЯ КОНФЛИКТА
  8. I.3. Основные этапы исторического развития римского права
  9. II. Метод упреждающего вписывания
  10. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  11. II. Методы непрямого остеосинтеза.
  12. II. Организация и этапы статистического исследования

1) Замена области непрерывного изменения аргумента дискретным множеством точек, называемых узлами сетки;

2) Аппроксимация производных в узлах конечно-разностными аналогами;

3) Аппроксимация дифференциального уравнения системой линейных или нелинейных разностных уравнений;

Решение полученной системы разностных уравнений.

Разностные методы позволяют находить только частное решение. Результат численного решения дифференциального уравнения представляется в виде таблицы 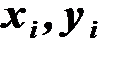. Аналитический вид решения 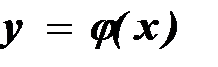может быть получен аппроксимацией.

Математические системы. Mathcad.

Mathcad – это многофункциональная интерактивная вычислительная система для аналитического и численного решения разнообразных математических задач и документирования результатов работы. Она включает следующие функциональные компоненты.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)