АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Затем находится уточненное окончательное значение

Читайте также:
  1. B) наиболее часто встречающееся значение признака в данном ряду
  2. I и II ополчения: их состав, значение.
  3. I. Понятие и значение охраны труда
  4. V. Grammatik. Wiederholen Sie die Grammatik zum Thema « Словообразование. Значение суффиксов »
  5. Write ('Значение В-',В)
  6. XI. ЦЕЛЬ МИРА И ЦЕЛЬ ЖИЗНИ (НАЗНАЧЕНИЕ ЧЕЛОВЕКА)
  7. XX съезд КПСС. Процесс политической реабилитации и десталинизации во второй половине 1950 – начале 1960-х гг. и его значение.
  8. А затем дважды в неделю в течение 2 мес.) является достаточно эффективной дополнительной терапией в
  9. А) исходное расположение; б) назначение позиционного допуска; в) указание предельных отклонений размеров, координирующих оси отверстий
  10. А) Спектр света и значение разного типа излучений
  11. А.) Значение Психической Энергии
  12. Абсолютное значение одного процента прироста

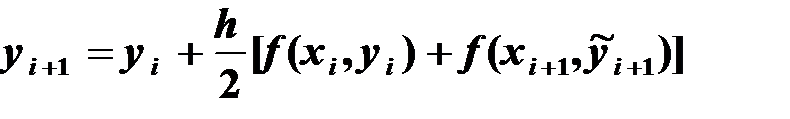(6.6)

Такая схема решения называется модифицированным методом Эйлера и имеет второй порядок точности.

Метод Рунге-Кутта.

Формулы (6.5-6.6) можно представить в виде

Где

Такая формулировка модифицированного метода Эйлера представляет собой метод Рунге-Кутта второго порядка. На основе метода Рунге-Кутта могут быть построены разностные схемы разного порядка точности. Наиболее употребительной является следующая схема четвертого порядка:

(6.7)

Где

(6.8)

Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения. Однако это окупается повышенной точностью, что дает возможность проводить счет с относительно большим шагом.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)