Если функция задана в виде полинома, то он называется интерполяционным полиномом и может быть записан, например, в форме Лагранжа или Ньютона

Интерполяционные многочлены Лагранжа

Пусть на некотором промежутке 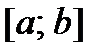заданы 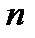различных узлов , , , …, , а также значения некоторой функции , , , …, в этих узлах. Необходимо построить полином , проходящий через заданные точки, т.е.

Интерполяционный полином Лагранжа имеет следующую формулу:

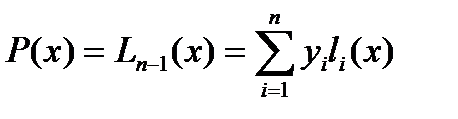
где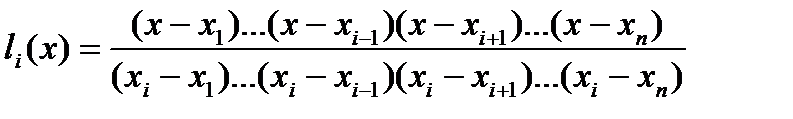

- фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам

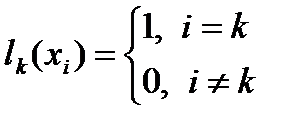
и зависят лишь от заданных узлов , но не от значений интерполируемой функции .

Интерполяционные многочлены Ньютона

Интерполяционный полином Ньютона имеет вид:

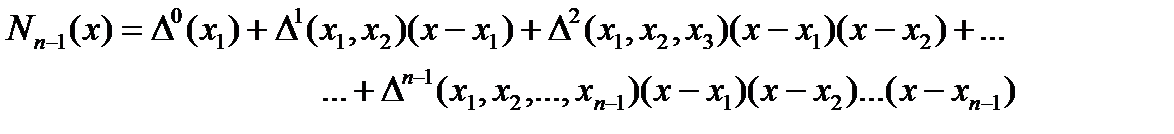
Где

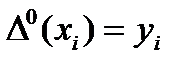
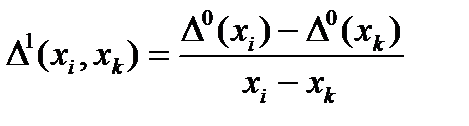- разделенная разность первого порядка,

- разделенная разность второго порядка,

- разделенная разность третьего порядка и т.д.

Поиск по сайту: