АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Для получения единственного решения задачи аппроксимации необходимо

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  3. I. Ситуационные задачи и тестовые задания.
  4. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  5. II. Основные задачи и функции
  6. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  7. II. Цель и задачи государственной политики в области развития инновационной системы
  8. III. Закупка у единственного поставщика.
  9. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  10. IV. Далее в этой лабораторной работе необходимо создать и сохранить запрос для отображения средних цен на все товары по таблице «Товары».
  11. MathCad: способы решения системы уравнений.
  12. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка

1. Задать общий вид аппроксимирующей функции, включающий неизвестные параметры. Вид функции задается, исходя из формы распределения аппроксимируемых значений, из предполагаемой функциональной зависимости, или просто в виде полинома некоторой степени;

Определить значения параметров на основе заданного критерия близости. Здесь существует два основных подхода – интерполяция и сглаживание(МНК).

Интерполяция.

Для задачи интерполяции критерий близости аппроксимирующей функции 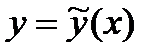к исходным данным 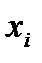, 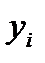рассматривается как совпадение значений в заданных точках, называемых узлами интерполяции, т.е.

.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)