Метод наименьших квадратов (МНК)

Аппроксимация на основе интерполяции не имеет смысла или невозможна, когда исходные данные содержат погрешности, повторы или очень большое количество точек. В этих случаях используют сглаживание: критерий близости аппроксимирующей функции к исходным данным , рассматривается как минимальное отклонение значений в заданных точках. Количественно отклонение может быть оценено методом наименьших квадратов (МНК), согласно которому необходимо минимизировать сумму квадратов:

где 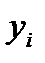_, - значения данных - значение аппроксимирующей функции в точке ; - число данных, - незвестные параметры. Задача сводится к нахождению экстремума функции параметров .

Линейная аппроксимация. В случае линейной формулы сумма квадратов принимает вид:

Эта ункция имеет минимум в точках, в которых частные производные от 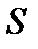по параметрам и обращаются в нуль, т.е.

,

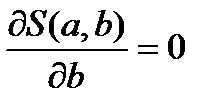
Решая систему уравнений, получим значения и уравнения .

Полиномиальная аппроксимация. В случае выбора зависимости в виде полинома, например, 2-й степени сумма квадратов принимает вид:

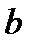Эта функция имеет минимум в точках, в которых частные производные от по параметрам , , обращаются в нуль, т.е.:

, ,

В результате дифференцирования и элементарных преобразований для определения параметров получают систему из трех линейных уравнений с тремя неизвестными:

Или

Поиск по сайту: