АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Шаг разбиения для равноотстоящих узлов определяем по формуле

Читайте также:
  1. Анатомо-физиологические особенности кожи, подкожной клетчатки, лимфатических узлов. Методика обследования. Семиотика.
  2. АНГИИТ УЗЛОВАТЫЙ
  3. Вещи индивидуальные и определяемые родовыми признаками, находящиеся в обороте и вне оборота по римскому праву.
  4. Гамма-функция точно определяется по формуле
  5. Генераторы транзитных и локальных узлов
  6. Если посмотреть на эту формулу более внимательно, то можно увидеть что соответствует формуле расчёта ВВП по расходам.
  7. Жилая площадь в районе определяется по формуле
  8. Зняття вузлових швів на фантомі
  9. Интерполяционные и экстраполяционные формулы при равноотстоящих значениях аргумента.
  10. Йогическая концепция психоэнергетических узлов
  11. КЛАССИФИКАЦИЯ ВОДНЫХ ПУТЕЙ СООБЩЕНИЙ И ГИДРОТЕХНИЧЕСКИХ УЗЛОВ
  12. Количество дежей, необходимое для приготовления полуфабрикатов, n, шт., рассчитывают по формуле

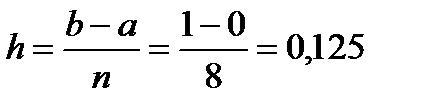
Сравнивая формулы, обратим внимание, что определенный интеграл приближенно можно вычислять по формуле

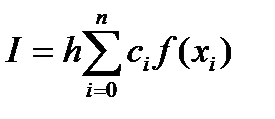
где - числовые коэффициенты, на которые умножаются значения функции в узлах :

- для метода левых прямоугольников;

- для метода правых прямоугольников;

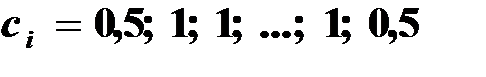- для метода трапеций;

- для метода парабол

Вычислим значения функции в узлах (табл. 5.3).

Таблица 5.3

  0,125 0,25 0,375 0,5 0,625 0,75 0,875  
1,000 1,016 1,061 1,132 1,225 1,335 1,458 1,591 1,732

Вычислим интеграл:

По формуле левых прямоугольников

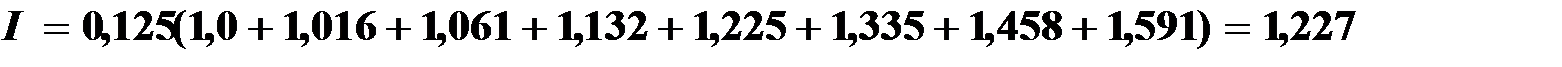
По формуле правых прямоугольников

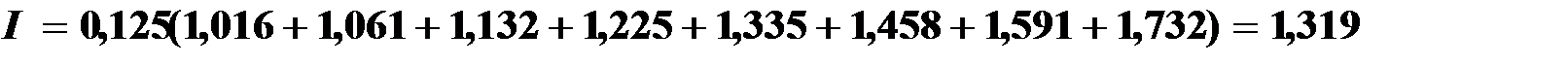
По формуле трапеций

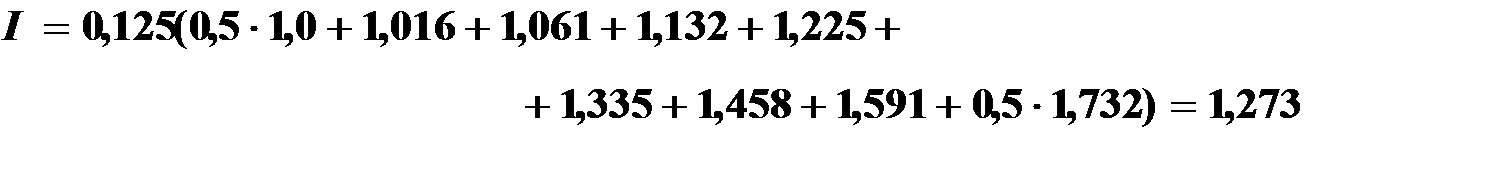
По формуле парабол

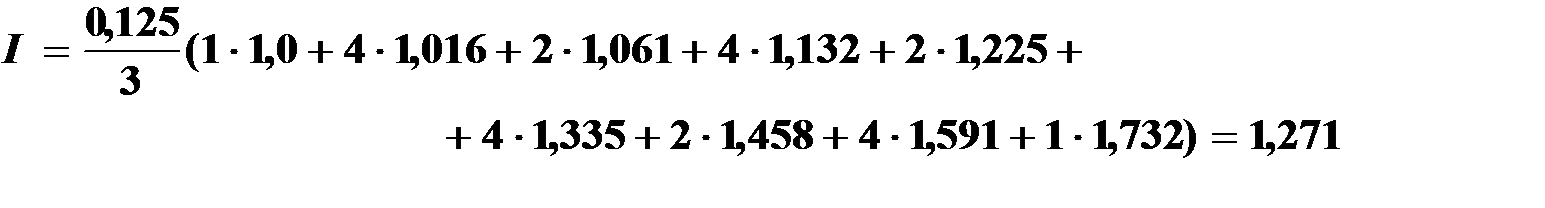
Численное дифференцирование


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)