АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Правило Рунге (Оценка точности вычисления определенного интеграла)

Читайте также:
  1. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  2. V2: Спектр атома водорода. Правило отбора
  3. Адаптивные программы вычисления определенных интегралов
  4. Алгоритм вычисления кодов Шеннона — Фано
  5. Алгоритм вычисления произведения
  6. Алгоритм Гаусса вычисления ранга матрицы
  7. Але монетарне правило не враховує мінливості швидкості обігу грошей та чутливості попиту до зміни процентної ставки.
  8. АНАЛИЗ БЕЗУБЫТОЧНОСТИ
  9. Анализ безубыточности
  10. Анализ безубыточности деятельности. Влияние на безубыточность деятельности производителей цены продукции, затрат на производство, объемов продаж
  11. Анализ безубыточности и оценка запаса финансовой прочности
  12. Анализ безубыточности и оценка запаса финансовой прочности

Погрешность вычисления значения интеграла 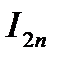при числе шагов , равном 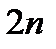, определяется по формуле Рунге:

- значения интеграла при числе шагов, равном ,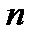

- порядок точности, равный 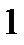для формулы левых (правых) прямоугольников, 2 для формулы трапеций и 4 для формулы Симпсона.

Таким образом, интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) для последовательных значений числа шагов , , 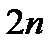, 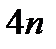и т.д. Процесс вычислений заканчивается, когда для очередного значения 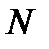будет выполнено условие 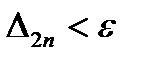, где ε ‑ заданная точность.

Пример 5.1. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол:

Решение. Выберем на отрезке интегрирования 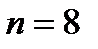различных узлов


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)