АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

При расчете удобно использовать таблицу

Читайте также:
  1. В отделении находится запас белья на сутки. Запрещается сушить белье на радиаторах центрального отопления и использовать его повторно.
  2. Витовт вёл двойную игру- с одной стороны он хотел использовать союз с Москвой против татар, а с другой стороны – использовать татар против Москвы.
  3. Вы можете использовать эту встречу для того, чтобы дать христианскую литературу тем подросткам, которые заинтересованы узнать больше об Иисусе или о христианской вере.
  4. Выявить знания, выходящие за предполагаемые границы проблемы, которые можно было бы использовать при трансформации проблемы.
  5. Где можно использовать рекламные листовки
  6. Для решения задачи следует использовать следующие сведения
  7. Задание 3. Заполнить таблицу
  8. ЗАДАНИЕ № 26. Создать и отформатировать таблицу с данными.
  9. Использование физико- механических свойств пищевых продуктов при расчете технологического оборудования.
  10. Как использовать жимовую майку
  11. КАК ИСПОЛЬЗОВАТЬ ОТВЛЕЧЕНИЕ, ЧТОБЫ ПЕРЕНАПРАВИТЬ РЕБЕНКА
  12. Как называется деформационная характеристика грунта при расчете конструкций на упругом основании
 
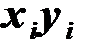
  -2     -8   -12  

Точность аппроксимации можно оценить среднеквадратической ошибкой

, которая не должна превышать погрешность исходных данных.

Формулы численного интегрирования Формулы прямоугольников и трапеций.

Численное интегрирование.

Требуется вычислить определенный интеграл:

Выберем на отрезке интегрирования различных узлов

и интерполируем функцию по ее значениям в этих узлах некоторым полиномом . Тогда определенный интеграл приближенно можно вычислять по формуле

,


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.706 сек.)