АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Модифицированный метод Эйлера

Читайте также:
  1. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Методические основы
  4. I. Методические основы оценки эффективности инвестиционных проектов
  5. I. Предмет и метод теоретической экономики
  6. I. Что изучает экономика. Предмет и метод экономики.
  7. II. Метод упреждающего вписывания
  8. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  9. II. Методы непрямого остеосинтеза.
  10. II. Проблема источника и метода познания.
  11. II. Рыночные методы.
  12. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ

Модифицированный метод Эйлера позволяет уменьшить погрешность на каждом шаге до величины 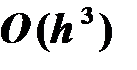вместо 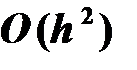в обычном методе (6.2). Запишем разложение функции в ряд Тейлора в виде:

(6.3)

Аппроксимируем вторую производную с помощью отношения конечных разностей:

Подставляя это соотношение в (6.3) и пренебрегая членами порядка 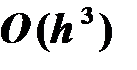, получаем:

(6.4)

Полученная схема является неявной, поскольку искомое значение входит в обе части соотношения (6.4), но можно построить приближенное решение с использованием двух итераций.

Сначала по формуле Эйлера (6.2) вычисляют первое приближение

(6.5)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)