Теорема обращения и ее приложения

Алгебраический подход в комбинаторике основан на использовании вспомогательных комбинаторных тождеств.

Пусть имеются два семейства комбинаторных чисел и , где ; .

Теорема 2.5.1. (теорема обращения)

Если для любого и имеет место разложение

, (2.5.1)

причем при , коэффициенты удовлетворяют соотношению

(2.5.2)

где – определенный набор комбинаторных чисел, то при справедливо разложение

. (2.5.3)

Доказательство:

Для правой части (2.5.3) с использованием соотношения (2.5.2) находим

.

Что и требовалось доказать. ■

В качестве комбинаторных чисел-коэффициентов , как правило, выбирают биномиальные коэффициенты , которые удовлетворяют следующим соотношениям:

1). - разложение бинома Ньютона; (2.5.4)

2). ; (2.5.5)

3). (2.5.6)

– свойство симметрии биномиальных коэффициентов;

4). (2.5.7)

– свойство суммы биномиальных коэффициентов.

Доказательство 4):

Из формулы (19) при находим . ■

5). (2.5.8)

–свойство суммы .

Доказательство 5):

Из формулы (19) , ,

Из формулы (19) . ■

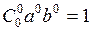6). (2.5.9)

– мультипликативное свойство.

Доказательство 6):

Используя выражение для через факториалы, находим:

,

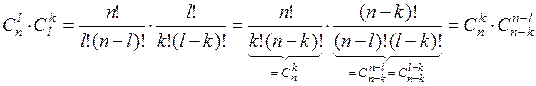что и требовалось доказать. ■

7). . (2.5.10)

Доказательство 7):

Используя соотношение (22), получаем:

что и требовалось доказать. ■

Сравнивая (2.5.10) и (2.5.2), коэффициенты и можно выбрать в виде

(2.5.11)

Доказательство:

Имеем:

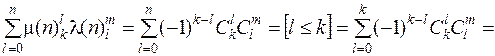
ф. (2.5.2),

что и требовалось доказать. ■

С учетом выбора (2.5.11), соотношения между числами и можно записать как

, (2.5.12)

где .

Применим этот результат для получения явных формул для чисел и .

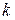Рассмотрим множество всех возможных отображений из -множества А в -множество В. Удобно изображать эти отображения в форме таблицы

:

Число различных отображений такого рода, очевидно, равно

. (2.5.13)

С другой стороны, это же число можно найти, используя и числа , выбирая из множества В для отображений сначала 1 элемент, затем 2 элемента и т.д. Поэтому получаем равенство

. (2.5.14)

С учетом доопределения суммирование можно начинать с 0. Тогда, используя равенство (2.5.12), находим:

, (2.5.15)

. (2.5.16)

Поиск по сайту: