АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

График линейной функции

Читайте также:
  1. B3.4. Правила оформления графиков
  2. II. Основные задачи и функции
  3. III. Предмет, метод и функции философии.
  4. IV. Конструкция бент-функции
  5. MathCad: построение, редактирование и форматирование графиков в декартовой системе координат.
  6. Ms Excel: мастер функций. Логические функции.
  7. V2: ДЕ 29 - Введение в анализ. Предел функции на бесконечности
  8. V2: ДЕ 32 - Дифференциальное исчисление функции одной переменной. Производная
  9. V2: ДЕ 35 - Дифференциальное исчисление функции одной переменной. Производные высший порядков
  10. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  11. V2: Функции исторической науки
  12. VIII. ФУНКЦИИ НАУЧНОГО ИССЛЕДОВАНИЯ

Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если , то

Берем еще какую-нибудь точку, например, 1.

Если 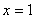, то

При оформлении заданий координаты точек обычно сводятся в таблицу:

Две точки найдены, выполним чертеж:

 

 

1) Линейная функция вида () называется прямой пропорциональностью. Например, . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

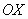2) Уравнение вида задает прямую, параллельную оси , в частности, сама ось 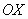задается уравнением . График функции строится сразу, без нахождения всяких точек. То есть, запись следует понимать так: «игрек всегда равен –4, при любом значении икс».

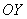3) Уравнение вида задает прямую, параллельную оси , в частности, сама ось 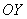задается уравнением . График функции также строится сразу. Запись 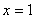следует понимать так: «икс всегда, при любом значении игрек, равен 1».


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)