График квадратичной, кубической функции, график многочлена

Парабола.

График квадратичной функции () представляет собой параболу. Рассмотрим знаменитый случай:

Вспоминаем некоторые свойства функции .

Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси 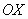мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: . Область определения любой функции стандартно обозначается через или 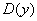. Буква обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву , а жирную букву R).

Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае: – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через или .

Функция является чётной. Если функция является чётной, то ее график симметричен относительно оси 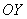. Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием . Как проверить любую функцию на чётность? Нужно вместо подставить в уравнение . В случае с параболой проверка выглядит так: 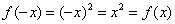, значит, функция является четной.

Функция не ограничена сверху. Аналитически свойство записывается так: .

Пример 2

Построить график функции .

Я рассмотрю важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто. Я предлагаю следующий алгоритм построения.

Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:

Итак, решение нашего уравнения: 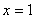– именно в этой точке и находится вершина параболы.. А пока рассчитываем соответствующее значение «игрек»:

Таким образом, вершина находится в точке

Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция – не является чётной, но, тем не менее, симметричность параболы никто не отменял.

В каком порядке находить остальные точки, думаю, будет понятно из итоговой таблицы:

Выполним чертеж:

Из рассмотренных графиков вспоминается еще один полезный признак:

Для квадратичной функции () справедливо следующее:

Если , то ветви параболы направлены вверх.

Если , то ветви параболы направлены вниз.

Поиск по сайту: