Кубическая парабола

Кубическая парабола задается функцией .

Перечислим основные свойства функции

Область определения – любое действительное число: .

Область значений – любое действительное число: .

Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»:
, значит, функция является нечетной.

Функция не ограничена. На языке пределов функции это можно записать так: ,

Кубическую параболу тоже эффективнее строить с помощью алгоритма представленного выше.

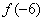Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении уже не нужно ничего считать, автоматом записываем, что 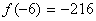. Эта особенность справедлива для любой нечетной функции.

Теперь немного поговорим о графиках многочленов.

График любого многочлена третьей степени () принципиально имеет следующий вид:

В этом примере коэффициент при старшей степени , поэтому график развёрнут «наоборот». Такой же вид имеют графики многочленов 5-ой, 7-ой, 9-ой и других нечетных степеней. Многочлены 4-ой, 6-ой и других четных степеней имеют график следующего вида:

График функции

Он представляет собой одну из ветвей параболы. Выполним чертеж:

Основные свойства функции :

Область определения: .

Область значений: .

То есть, график функции полностью находится в первой координатной четверти.

Функция не ограничена сверху. Или с помощью предела:

При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:

Поиск по сайту: