 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Математическая модель регулярной линии передачи
Наиболее простая теория, описывающая работу линии передачи с волной типа Т была построена очень давно и уравнения, описывающие процессы в такой линии, получили название телеграфных уравнений. Это система двух дифференциальных уравнений 1-го порядка. Они вводят понятие токов и напряжений в линии.
В этой теории линия передачи представляется последовательностью периодически повторяющихся L, R и C, G цепочек.
Рис.2.1. Эквивалентная схема отрезка линии длиной 
здесь R – погонное сопротивление и G – погонная проводимость характеризуют, соответственно, потери в металле и в диэлектрике, L – погонная индуктивность; C погонная емкость.
Уравнения длинной линии имеют вид:
где V и I мгновенные значения напряжения и тока.
Если временная зависимость полей вводится как 
, то
Решение этих уравнений имеет вид:
(2.5.)
где 
; 
.
При отсутствии потерь
; 
(2.6)
β - коэффициент фазы (м-1), связанный с длинной волны в линии передачи λв, круговой частотой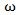 
и фазовой скоростью vф соотношением:
Учитывая, что погонная индуктивность L меняется при изменении геометрии линии в меньшей степени чем погонная емкость С, легко, используя (2.6) понять, как изменяется zв при изменении геометрии линии.
Введем далее обозначения:
где 
– комплексная амплитуда волны напряжения, распространяющейся в сторону увеличения координаты x (падающая волна).
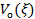- комплексная амплитуда волны напряжения, распространяющейся в линии навстречу падающей, эта волна носит название отраженной.
Тогда полные напряжения и ток в сечении линии x могут быть записаны как
(2.7)
Падающая и отраженная волны движутся навстречу друг другу с изменяющейся фазой, в результате чего в распределении напряжения и тока вдоль тракта возникают максимумы и минимумы.
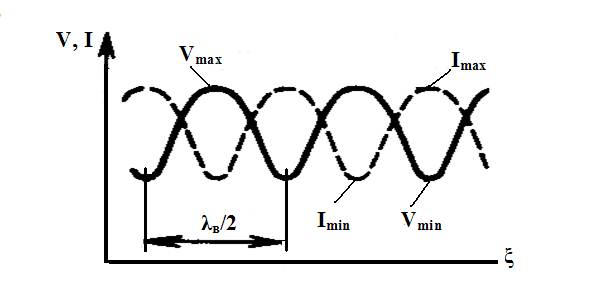
Рис.2.2 Распределение напряжения и тока вдоль линии
Отношение 
называется коэффициентом отражения по напряжению и обозначается как 
.
(2.8)
Так как напряжения падающей и отраженной волн пропорциональны поперечным компонентам соответствующих электрических полей и имеют одинаковые с ними фазы, то коэффициент отражения по напряжению совпадает с коэффициентом отражения по электрическому полю.
Учитывая (2.8) выражения для напряжения и тока можно записать в виде
(2.9)
Принимая, что
где 
и 
значения комплексных амплитуд падающей и отраженной волн в некотором сечении 
можно записать, что
При отсутствии потерь (α=0)
Из (2.9) следует, что напряжение в максимуме равно:
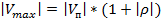
(2.10)
Отношение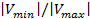 
называется коэффициентом бегущей волны КБВ, обратное отношение - коэффициентом стоячей волны КСВ. Учитывая (2.10) можно записать
Отсюда следует, что КБВ в линии меняется от 1 до 0 при изменении коэффициента отражения от 0 до 1, а КСВ соответственно от 1 до бесконечности.
Отношение напряжения к току в некотором сечении ξ линии называется эквивалентным полным сопротивлением линии в этом сечении
(2.11)
Эквивалентное полное сопротивление в заданном сечении имеет тот физический смысл, что оно является входным сопротивлением отрезка линии длиной, равной расстоянию от сечения 
до сечения входа нагрузки, с подключенной на конце нагрузкой.
На практике вместо продольной координаты ξ удобно ввести координату 
с нулевым значением в некотором произвольном сечении линии и положительным отсчетом в направлении от нагрузки к генератору (рис.2.3)
Рис.2.3 Замена продольной координаты
В этом случае соотношения (2.9) для тока и напряжения выглядят следующим образом
(2.12)
коэффициент отражения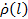 
имеет соответственно вид
При отсутствии в линии потерь (α=0)
Отсюда коэффициент отражения в сечении 
может быть определен через известное значение в сечении 
с помощью соотношения
(2.13)
где 
положительно, если сдвиг от сечения осуществляется в сторону генератора, и отрицательно, если сдвиг в сторону к нагрузке.
Из (2.13) следует, что в линии без потерь модуль коэффициента отражения не зависит от координаты , а фаза меняется от 0 до 2π на интервале, равном половине длины волны в линии.
Теперь можно связать значение сопротивления нагрузки в сечениях и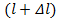 
Используя для экспоненты представление
получаем
Поделим числитель и знаменатель на величину 
.
С учетом того, что
получаем соотношение, связывающее сопротивления в сечениях линии и 
(2.14)
Для проводимости аналогично можно получить представленное ниже выражение
(2.15)
Поиск по сайту: