Доказательство. ( с учетом того, что если Dx®0, то Du®0, т.к

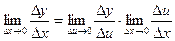
(с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)

Тогда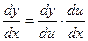

Теорема доказана.

Логарифмическое дифференцирование.

Рассмотрим функцию .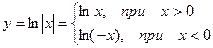

Тогда (lnïxï)¢= , т.к. .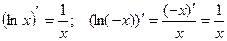

Учитывая полученный результат, можно записать .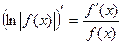

Отношение называется логарифмической производной функции f(x).

Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

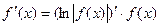
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.

Производная показательно- степенной функции.

Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.

Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.

Найдем производную функции y = u^v. Логарифмируя, получим:

lny = vlnu

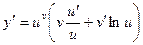
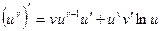
Пример. Найти производную функции .

По полученной выше формуле получаем:

Производные этих функций: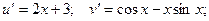

Окончательно:

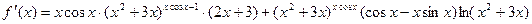
Производная обратных функций.

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g(y) по х:

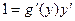
т.к. g¢(y) ¹ 0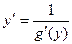

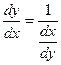
т.е. производная обратной функции обратна по величине производной данной функции.

Пример. Найти формулу для производной функции arctg.

Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом:

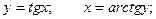
Известно, что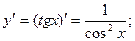

По приведенной выше формуле получаем:

Т.к. то можно записать окончательную формулу для производной арктангенса:

Таким образом получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.

Дифференциал функции.

Пусть функция y = f(x) имеет производную в точке х:

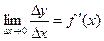
Тогда можно записать: , где a®0, при Dх®0.

Следовательно: .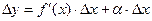

Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.

Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.

Обозначается dy или df(x).

Из определения следует, что dy = f¢(x)Dx или

dy = f¢(x)dx.

Можно также записать: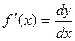

Геометрический смысл дифференциала.

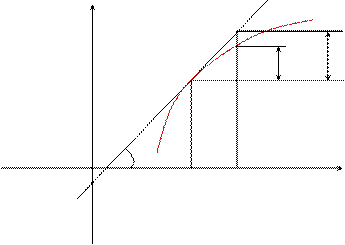y

f(x)

K

dy

M Dy

L

a

x x + Dx x

Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx

Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Свойства дифференциала.

Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv

2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv

3) d(Cu) = Cdu

4)

Дифференциал сложной функции.

Инвариантная форма записи дифференциала.

Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f¢(x)g¢(t)dt = f¢(x)dx.

Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

Однако, если х- независимая переменная, то

dx = Dx, но

если х зависит от t, то Dх ¹ dx.

Таким образом форма записи dy = f¢(x)Dx не является инвариантной.

Пример. Найти производную функции .

Сначала преобразуем данную функцию: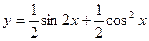

Пример. Найти производную функции .

Пример. Найти производную функции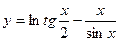

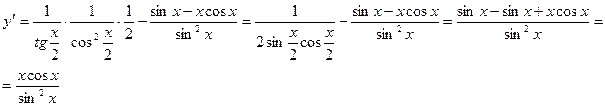
Пример. Найти производную функции

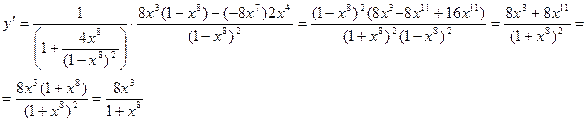
Пример. Найти производную функции

Формула Тейлора.

Поиск по сайту: