 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Способ. Метод неопределенных коэффициентов
Рассмотрим интегралы следующих трех типов:
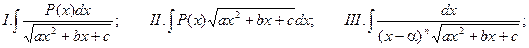
где P(x) – многочлен, n – натуральное число.
Причем интегралы II и III типов могут быть легко приведены к виду интеграла I типа.
Далее делается следующее преобразование:

в этом выражении Q(x)- некоторый многочлен, степень которого ниже степени многочлена P(x), а l - некоторая постоянная величина.
Для нахождения неопределенных коэффициентов многочлена Q(x), степень которого ниже степени многочлена P(x), дифференцируют обе части полученного выражения, затем умножают на 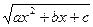 и, сравнивая коэффициенты при одинаковых степенях х, определяют l и коэффициенты многочлена Q(x).
и, сравнивая коэффициенты при одинаковых степенях х, определяют l и коэффициенты многочлена Q(x).
Данный метод выгодно применять, если степень многочлена Р(х) больше единицы. В противном случае можно успешно использовать методы интегрирования рациональных дробей, рассмотренные выше, т.к. линейная функция является производной подкоренного выражения.
Пример.
 .
.
Теперь продифференцируем полученное выражение, умножим на 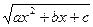 и сгруппируем коэффициенты при одинаковых степенях х.
и сгруппируем коэффициенты при одинаковых степенях х.
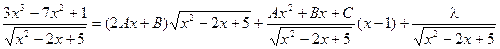
 =
= 
 =
= 


Итого  =
=
= 
Пример.








Пример.






Второй способ решения того же самого примера.

С учетом того, что функции arcsin и arccos связаны соотношением  , а постоянная интегрирования С – произвольное число, ответы, полученные различными методами, совпадают.
, а постоянная интегрирования С – произвольное число, ответы, полученные различными методами, совпадают.
Как видно, при интегрировании иррациональных функций возможно применять различные рассмотренные выше приемы. Выбор метода интегрирования обуславливается в основном наибольшим удобством, очевидностью применения того или иного метода, а также сложностью вычислений и преобразований.
Пример.

Несколько примеров интегралов, не выражающихся через
элементарные функции.
К таким интегралам относится интеграл вида  , где Р(х)- многочлен степени выше второй. Эти интегралы называются эллиптическими.
, где Р(х)- многочлен степени выше второй. Эти интегралы называются эллиптическими.
Если степень многочлена Р(х) выше четвертой, то интеграл называется ультраэллиптическим.
Если все – таки интеграл такого вида выражается через элементарные функции, то он называется псевдоэллиптическим.
Не могут быть выражены через элементарные функции следующие интегралы:
1)  - интеграл Пуассона (Симеон Дени Пуассон – французский математик (1781-1840))
- интеграл Пуассона (Симеон Дени Пуассон – французский математик (1781-1840))
2)  - интегралы Френеля (Жан Огюстен Френель – французский ученый (1788-1827) - теория волновой оптики и др.)
- интегралы Френеля (Жан Огюстен Френель – французский ученый (1788-1827) - теория волновой оптики и др.)
3)  - интегральный логарифм
- интегральный логарифм
4)  - приводится к интегральному логарифму
- приводится к интегральному логарифму
5)  - интегральный синус
- интегральный синус
6)  - интегральный косинус
- интегральный косинус
Определенный интеграл.
Пусть на отрезке [a, b] задана непрерывная функция f(x).
 y
y
M
m
0 a xi b x
Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]
Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.
x0 < x1 < x2 < … < xn
Тогда x1 – x0 = Dx1, x2 – x1 = Dx2, …,xn – xn-1 = Dxn;
На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции.
[x0, x1] ® m1, M1; [x1, x2] ® m2, M2; … [xn-1, xn] ® mn, Mn.
Составим суммы:
 n = m1Dx1 + m2Dx2 + … +mnDxn =
n = m1Dx1 + m2Dx2 + … +mnDxn = 
 n = M1Dx1 + M2Dx2 + … + MnDxn =
n = M1Dx1 + M2Dx2 + … + MnDxn = 
Сумма  называется нижней интегральной суммой, а сумма
называется нижней интегральной суммой, а сумма  – верхней интегральной суммой.
– верхней интегральной суммой.
Т.к. mi £ Mi, то  n £
n £  n, а m(b – a) £
n, а m(b – a) £  n £
n £  n £ M(b – a)
n £ M(b – a)
Внутри каждого отрезка выберем некоторую точку e.
x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].
Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn = 
Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi
Следовательно, 

Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.
Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.
Если  , то
, то 
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма  стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
Обозначение: 
а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции f(x) существует предел 
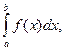 то функция называется интегрируемой на отрезке [a, b].
то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения: 

Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
1) 
2) 
3) 
4) Если f(x) £ j(x) на отрезке [a, b] a < b, то 
5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что

Доказательство: В соответствии со свойством 5:
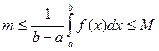
т.к. функция f(x) непрерывна на отрезке [a, b], то она принимает на этом отрезке все значения от m до М. Другими словами, существует такое число eÎ [a, b], что если
 и m = f(e), а a £ e £ b, тогда
и m = f(e), а a £ e £ b, тогда  . Теорема доказана.
. Теорема доказана.
7) Для произвольных чисел a, b, c справедливо равенство:

Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.
8) 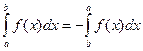
Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке [a, b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что

Вычисление определенного интеграла.
Пусть в интеграле  нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
Обозначим  = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.
= Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.

Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то

это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция  - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
- первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то

при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:



Тогда  .
.
А при х = b: 
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:

Теорема доказана.
Иногда применяют обозначение F(b) – F(a) = F(x)  .
.
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
Замена переменных.
Пусть задан интеграл  , где f(x) – непрерывная функция на отрезке [a, b].
, где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t).
Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то

Тогда 
Пример.

При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.
Пример.
 , с другой стороны, если применить тригонометрическую подстановку,
, с другой стороны, если применить тригонометрическую подстановку,

Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная tgx имеет на отрезке интегрирования разрыв (в точке х = p/2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
Интегрирование по частям.
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше, поэтому здесь приводить его нет смысла.
Приближенное вычисление определенного интеграла.
Как было сказано выше, существует огромное количество функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подинтегральная функция заменяется “близкой” к ней функцией, интеграл от которой выражается через элементарные функции.
Формула прямоугольников.
Если известны значения функции f(x) в некоторых точках x0, x1, …, xm, то в качестве функции “близкой” к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.

Если разбить отрезок интегрирования на n равных частей  . При этом:
. При этом:
y0 = f(x0), y1 = f(x1), …., yn = f(xn).
Составим суммы: y0Dx + y1Dx + … + yn-1Dx
y1Dx + y2Dx + … + ynDx
Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной.
Тогда  или
или
 - любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.
- любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.
Формула трапеций.
Эта формула является более точной по
 у сравнению с формулой прямоугольников.
у сравнению с формулой прямоугольников.
Подинтегральная функция в этом случае
заменяется на вписанную ломаную.
y1 у2 уn
a x1 x2 b x
Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.
Площади вписанных трапеций вычисляются по формулам:
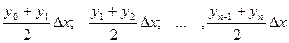

После приведения подобных слагаемых получаем формулу трапеций:

Формула парабол
(формула Симпсона или квадратурная формула).
(Томас Симпсон (1710-1761)- английский математик)
Разделим отрезок интегрирования [a, b] на четное число отрезков (2m). Площадь криволинейной трапеции, ограниченной графиком функции f(x) заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями f(x0), f(x1), f(x2).
Для каждой пары отрезков построим такую параболу.
 у
у
0 х0 х1 х2 х3 х4 х
Уравнения этих парабол имеют вид Ax2 + Bx + C, где коэффициенты А, В, С могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
 (1)
(1)
Обозначим  .
.

Если принять х0 = -h, x1 = 0, x2 = h, то 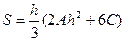 (2)
(2)
Тогда уравнения значений функции (1) имеют вид:

C учетом этого:  .
.
Отсюда уравнение (2) примет вид: 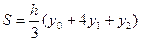
Тогда

Складывая эти выражения, получаем формулу Симпсона:

Чем больше взять число m, тем более точное значение интеграла будет получено.
Пример. Вычислить приближенное значение определенного интеграла
 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей.
По формуле Симпсона получим:

| m | |||||||||||
| x | -2 | -1 | |||||||||
| f(x) | 2.828 | 3.873 | 4.123 | 4.899 | 6.557 | 8.944 | 11.874 | 15.232 | 18.947 | 22.978 |

Точное значение этого интеграла – 91.173.
Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.
Для сравнения применим к этой же задаче формулу трапеций.

Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая вычисляет любой определенный интеграл всеми рассмотренными выше методами.
 |
Для запуска программы дважды щелкните на значке
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Кроме вышеперечисленных способов, можно вычислить значение определенного интеграла с помощью разложения подинтегральной функции в степенной ряд.
Принцип этого метода состоит в том, чтобы заменить подинтегральную функцию по формуле Тейлора и почленно проинтегрировать полученную сумму.
Пример. С точностью до 0,001 вычислить интеграл

Т.к. интегрирование производится в окрестности точки х =0, то можно воспользоваться для разложения подинтегральной функции формулой Маклорена.
Разложение функции cos x имеет вид:

Зная разложение функции cos х легко найти функцию 1 – cos x:

В этой формуле суммирование производится по п от 1 до бесконечности, а в предыдущей – от 0 до бесконечности. Это – не ошибка, так получается в результате преобразования.
Теперь представим в виде ряда подинтегральное выражение.

Теперь представим наш интеграл в виде:

В следующем действии будет применена теорема о почленном интегрировании ряда. (Т.е. интеграл от суммы будет представлен в виде суммы интегралов членов ряда).
Вообще говоря, со строго теоретической точки зрения для применения этой теоремы надо доказать, что ряд сходится и, более того, сходится равномерно на отрезке интегрирования [0, 0,5]. Эти вопросы будут подробно рассмотрены позже (См. Действия со степенными рядами.) Отметим лишь, что в нашем случае подобное действие справедливо хотя бы по свойствам определенного интеграла (интеграл от суммы равен сумме интегралов).
Итак:

Итого, получаем:

Как видно, абсолютная величина членов ряда очень быстро уменьшается, и требуемая точность достигается уже при третьем члене разложения.
Для справки: Точное (вернее – более точное) значение этого интеграла: 0,2482725418…
При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая вычисляет любой определенный интеграл с помощбю степенных рядов и выводит подробный отчет о ходе решения.
 |
Для запуска программы дважды щелкните на значке
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Несобственные интегралы.
Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].
Определение: Если существует конечный предел  , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение: 
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:


Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
 - не существует.
- не существует.
Несобственный интеграл расходится.
Пример.
 - интеграл сходится
- интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие  и интеграл
и интеграл  сходится, то
сходится, то 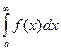 тоже сходится и
тоже сходится и  ³
³ 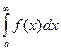 .
.
Теорема: Если для всех х (x ³ a) выполняется условие  и интеграл
и интеграл  расходится, то
расходится, то 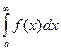 тоже расходится.
тоже расходится.
Теорема: Если 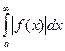 сходится, то сходится и интеграл
сходится, то сходится и интеграл 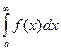 .
.
В этом случае интеграл 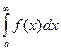 называется абсолютно сходящимся.
называется абсолютно сходящимся.
Интеграл от разрывной функции.
Если в точке х = с функция либо неопределена, либо разрывна, то

Если интеграл  существует, то интеграл
существует, то интеграл  - сходится, если интеграл
- сходится, если интеграл  не существует, то
не существует, то  - расходится.
- расходится.
Если в точке х = а функция терпит разрыв, то  .
.
Если функция f(x) имеет разрыв в точке b на промежутке [a, с], то

Таких точек внутри отрезка может быть несколько.
Если сходятся все интегралы, входящие в сумму, то сходится и суммарный интеграл.
Геометрические приложения определенного интеграла.
Вычисление площадей плоских фигур.
 |
у
+ +
0 a - b x
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула  .
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.


Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
 (ед2)
(ед2)
Нахождение площади криволинейного сектора.
 |
r = f(j)
b
a
О r
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид r = f(j), где r - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а j - угол наклона этого радиус – вектора к полярной оси.
Подробнее о полярной системе координат и ее связи с декартовой прямоугольной системой координат см. Полярная система координат. “Курс высшей математики. Часть 1.”
Площадь криволинейного сектора может быть найдена по формуле

Вычисление длины дуги кривой.
 y y = f(x)
y y = f(x)
DSi Dyi
Dxi
a b x
Длина ломаной линии, которая соответствует дуге, может быть найдена как  .
.
Тогда длина дуги равна  .
.
Из геометрических соображений: 
В то же время 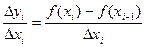
Тогда можно показать (см. Интегрируемая функция.), что

Т.е. 
Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем
 ,
,
где х = j(t) и у = y(t).
Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

Если кривая задана в полярных координатах, то
 , r = f(j).
, r = f(j).
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
1 способ. Выразим из уравнения переменную у. 
Найдем производную 
Тогда 
Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r,  тогда
тогда

Вычисление объемов тел.
Вычисление объема тела по известным площадям его параллельных сечений.

Q(xi-1)
Q(xi)
a xi-1 xi b x
Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [xi-1, xi] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Mi и mi.
Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны MiDxi и miDxi здесь Dxi = xi - xi-1.
Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно  и
и  .
.
При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:

Таким образом, объем тела может быть найден по формуле:

Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.
Пример: Найти объем шара радиуса R.
y

R y
-R 0 x R x
В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле  .
.
Тогда функция площадей сечений имеет вид: Q(x) =  .
.
Получаем объем шара:
 .
.
Пример: Найти объем произвольной пирамиды с высотой Н и площадью основания S.
 |
Q S
x H x
При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.

Отсюда получаем функцию площадей сечений: 
Находим объем пирамиды: 
Объем тел вращения.
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
 y = f(x)
y = f(x)
x
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса  , то объем тела вращения может быть легко найден по полученной выше формуле:
, то объем тела вращения может быть легко найден по полученной выше формуле:

Площадь поверхности тела вращения.
 Мi B
Мi B
А
х
xi
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, …, Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DPi. Эта площадь может быть найдена по формуле:

Здесь DSi – длина каждой хорды.

Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению  .
.
Получаем: 
Тогда 
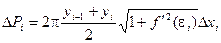
Площадь поверхности, описанной ломаной равна:

Эта сумма не является интегральной, но можно показать, что

Тогда 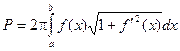 - формула вычисления площади поверхности тела вращения относительно оси Ох.
- формула вычисления площади поверхности тела вращения относительно оси Ох.
Заметим, что уравнение поверхности вращения относительно оси Ох имеет вид
y2 + z2 = f2(x).
Функции нескольких переменных
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.
z = f(x, y)
Определение: Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.
Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Определение: Окрестностью точки М0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию 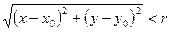 .
.
Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М0(х0, у0), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие
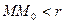
также верно и условие 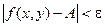 .
.
Записывают: 
Определение: Пусть точка М0(х0, у0) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М0(х0, у0), если
 (1)
(1)
причем точка М(х, у) стремится к точке М0(х0, у0) произвольным образом.
Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:
1) Функция z = f(x, y) не определена в точке М0(х0, у0).
2) Не существует предел  .
.
3) Этот предел существует, но он не равен f(x0, y0).
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой и
ограниченной области D, то в этой области найдется по крайней мере одна точка
N(x0, y0, …), такая, что для остальных точек верно неравенство
f(x0, y0, …) ³ f(x, y, …)
а также точка N1(x01, y01, …), такая, что для всех остальных точек верно неравенство
f(x01, y01, …) £ f(x, y, …)
тогда f(x0, y0, …) = M – наибольшее значение функции, а f(x01, y01, …) = m – наименьшее значение функции f(x, y, …) в области D.
Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка
N0(x0, y0, …) такая, что f(x0, y0, …) = m.
Проще говоря, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция по крайней мере один раз обращается в ноль.
Свойство. Функция f(x, y, …), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство  .
.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х1, y1) и (х2, у2) области, находящихся на расстоянии, меньшем D, выполнено неравенство

Приведенные выше свойства аналогичны свойствам функций одной переменной, непрерывных на отрезке. См. Свойства функций, непрерывных на отрезке.
Производные и дифференциалы функций
нескольких переменных.
Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина Dxz = f(x + Dx, y) – f(x, y) называется частным приращением функции по х.
Можно записать
 .
.
Тогда  называется частной производной функции z = f(x, y) по х.
называется частной производной функции z = f(x, y) по х.
Обозначение: 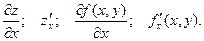
Аналогично определяется частная производная функции по у.

Геометрическим смыслом частной производной (допустим  ) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
) является тангенс угла наклона касательной, проведенной в точке N0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
Полное приращение и полный дифференциал.
Определение. Для функции f(x, y) выражение Dz = f(x + Dx, y + Dy) – f(x, y) называется полным приращением.
Если функция f(x, y) имеет непрерывные частные производные, то

Применим теорему Лагранжа (см. Теорема Лагранжа.) к выражениям, стоящим в квадратных скобках.

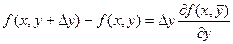
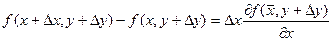
здесь 
Тогда получаем

Т.к. частные производные непрерывны, то можно записать равенства:


Определение. Выражение  называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
называется полным приращением функции f(x, y) в некоторой точке (х, у), где a1 и a2 – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.
Определение: Полным дифференциалом функции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).

Для функции произвольного числа переменных:

Пример. Найти полный дифференциал функции  .
.



Пример. Найти полный дифференциал функции 



Геометрический смысл полного дифференциала.
Касательная плоскость и нормаль к поверхности.
 нормаль
нормаль
N
j N0
касательная плоскость
Пусть N и N0 – точки данной поверхности. Проведем прямую NN0. Плоскость, которая проходит через точку N0, называется касательной плоскостью к поверхности, если угол между секущей NN0 и этой плоскостью стремится к нулю, когда стремится к нулю расстояние NN0.
Определение. Нормалью к поверхности в точке N0 называется прямая, проходящая через точку N0 перпендикулярно касательной плоскости к этой поверхности.
В какой – либо точке поверхность имеет, либо только одну касательную плоскость, либо не имеет ее вовсе.
Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М0(х0, у0), касательная плоскость в точке N0(x0,y0,(x0,y0)) существует и имеет уравнение:
 .
.
Уравнение нормали к поверхности в этой точке:

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке (х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Dх, у0+Dу).
Как видно, геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
Пример. Найти уравнения касательной плоскости и нормали к поверхности

в точке М(1, 1, 1).
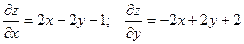

Уравнение касательной плоскости:

Уравнение нормали:

Приближенные вычисления с помощью полного дифференциала.
Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:


Если подставить в эту формулу выражение

то получим приближенную формулу:

Пример. Вычислить приближенно значение  , исходя из значения функции
, исходя из значения функции 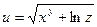 при x = 1, y = 2, z = 1.
при x = 1, y = 2, z = 1.
Из заданного выражения определим Dx = 1,04 – 1 = 0,04, Dy = 1,99 – 2 = -0,01,
Dz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) = 
Находим частные производные:



Полный дифференциал функции u равен:



Точное значение этого выражения: 1,049275225687319176.
При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая решает рассмотренный выше пример для произвольной функции трех переменных.
 |
Для запуска программы дважды щелкните на значке
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Частные производные высших порядков.
Если функция f(x, y) определена в некоторой области D, то ее частные производные  и
и  тоже будут определены в той же области или ее части.
тоже будут определены в той же области или ее части.
Будем называть эти производные частными производными первого порядка.
Производные этих функций будут частными производными второго порядка.


Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
Определение. Частные производные вида 
 и т.д. называются смешанными производными.
и т.д. называются смешанными производными.
Теорема. Если функция f(x, y) и ее частные производные  определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:
определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:
 .
.
Т.е. частные производные высших порядков не зависят от порядка дифференцирования.
Аналогично определяются дифференциалы высших порядков.
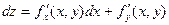


…………………

Здесь n – символическая степень производной, на которую заменяется реальная степень после возведения в нее стоящего в скобках выражения.
При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая находит все производные до второго порядка включительно для функции двух переменных.
Поиск по сайту: