Импульс тела. Закон сохранения механической энергии

Импульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:
Закон сохранения импульса утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.., при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
находят применение при создании современной ракетно-космической техники. Движение с помощью реактивной струи по закону сохранения импульса лежит в основе гидрореактивного двигателя. В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактивный принцип.

Снова обратимся к простой системе тел, состоящей из земного шара и поднятого над Землей тела, например камня.
Камень падает под действием силы тяжести. Силу сопротивления воздуха учитывать не будем. Работа, совершаемая силой тяжести при перемещении камня из одной точки в другую, равна изменению (увеличению) кинетической энергии камня:

В то же время эта работа равна уменьшению потенциальной энергии:

Работа силы всемирного тяготения, действующей со стороны камня на Землю, практически равна нулю. Из-за большой массы Земли ее перемещением и изменениемскорости можно пренебречь. Так как в формулах (6.24) и (6.25) левые части одинаковы, то равны и правые части:

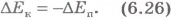
Равенство (6.26) означает, что увеличение кинетической энергии системы равно убыли ее потенциальной энергии (или наоборот). Отсюда вытекает, что

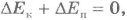
или

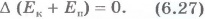
Изменение суммы кинетической и потенциальной энергий системы равно нулю.
Величину E, равную сумме кинетической и потенциальной энергий системы, называют механической энергией системы:

Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (6.27) равно нулю, то энергия остается постоянной:

Таким образом, в изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется. В этом состоит закон сохранениямеханической энергии. Энергия не создается и не уничтожается, а только превращается из одной формы в другую: из кинетической в потенциальную и наоборот.
Учитывая, что в рассматриваемом конкретном случае и , можно закон сохранения механической энергии записать так:

или

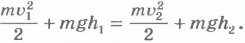
Это уравнение позволяет очень просто найти скорость камня v₂ на любой высоте h₂ над землей, если известна начальная скорость v₁ камня на исходной высоте h₁.
Закон сохранения механической энергии (6.29) легко обобщается на случай любого числа тел и любых консервативных сил взаимодействия между ними. Под E_к нужно понимать сумму кинетических энергий всех тел, а под Е_п - полную потенциальную энергию системы.
Для системы, состоящей из тела массой m и пружины, закон сохранения механической энергии имеет вид

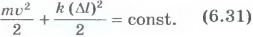
Полная механическая энергия системы равна сумме ее кинетической и потенциальной энергий. В изолированной системе, в которой действуют только консервативные силы, механическая энергия сохраняется.

Поиск по сайту: