 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Комбінації
|
Читайте также: |
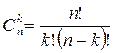 .
. 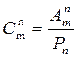 .
.
1) З 12 членів туристичної групи потрібно вибрати трьох чергових. Скількома способами можна виконати цей вибір?
Коментар
Оскільки порядок слідування елементів не враховується (для чергових не важливо, у якому порядку їх виберуть), то відповідна сполука є комбінацією з 12 елементів по 3 (без повторень). Для обчислення можна використати формулу: 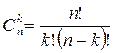
| Розв’язання
Кількість способів вибрати з 12 туристів трьох чергових дорівнює кількості комбінацій з 12 елементів по 3 (без повторень), тобто  Відповідь: 220.
Відповідь: 220.
|
2) Із вази з фруктами, у якій лежать 10 різних яблук і 5 різних груш, потрібно вибрати 2 яблука і 3 груші. Скількома способами можна виконати такий вибір?
Коментар
Спочатку окремо виберемо 2 яблука з 10 і 3 груші з 5. оскільки при виборі яблук і груш порядок слідування елементів не враховується, то відповідні сполуки – комбінації без повторень.
Враховуючи, що потрібно вибрати і 2 яблука, і 3 груші, використовуємо правило добутку і перемножуємо одержані можливості вибору яблук ( ) і груш ( ) і груш (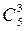 ). ).
| Розв’язання
Вибрати 2 яблука з 10 можна  способами. При кожному виборі яблук груші можна вибрати способами. При кожному виборі яблук груші можна вибрати 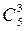 способами. Тоді за правилом добутку вибір потрібних фруктів можна виконати способами. Тоді за правилом добутку вибір потрібних фруктів можна виконати  × × 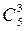 способами. Одержуємо: способами. Одержуємо:
 × × 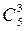 = = 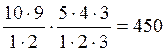 Відповідь: 450.
Відповідь: 450.
|
3) Обчислити: 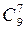 .
.

4) Скількома способами можна розподілити уроки в шести класах між трьома вчителями, якщо кожний учитель викладатиме у двох класах?
Розв’язання:
Перший учитель може вибрати два класи з шести 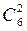 різними способами. Після вибору першого вчителя другий може вибрати два класи з чотирьох, що залишилися,
різними способами. Після вибору першого вчителя другий може вибрати два класи з чотирьох, що залишилися, 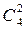 різними способами. Тоді два вчителя можуть вибрати два класи
різними способами. Тоді два вчителя можуть вибрати два класи 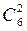 ×
× 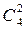 різними способами. Якщо вони вже зробили вибір, то третій може взяти лише ті два класи, що залишилися. Тому шукане число способів дорівнює:
різними способами. Якщо вони вже зробили вибір, то третій може взяти лише ті два класи, що залишилися. Тому шукане число способів дорівнює: 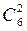 ×
× 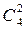 =
=  .
.
Відповідь: 90.
Поиск по сайту: