Денелерді жылжымайтын цилиндрлік топсамен байланыстыру

Бұл денені топсалы байланыстан босату кезінде реакция күшін және 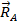құраушыларға жіктейді. Оның толық реакциясының модульі мен бағыты мына формуламен анықталады:

; ;

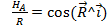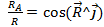
мұнда , -тіктөртбұрышты декарттық координаталар осьтерінің бірлік векторлары.

4.3-сурет. Жылжымайтын топса арқылы байланыс.

4. Денелерді жылжымалы топса арқылы байланыстыру. Жылжымалы топса дененің тіреу жазықтығы бетімен қозғалыс жасауына кедергі келтірмейді және тіреуге перпендикуляр бағытта қозғалысын шектейді. Сондықтан реакция күші топса арқылы өтіп әр уақытта тіреу жазықтығына перпендикуляр бағытталады.

4.4-сурет. Жылыжымалы топсалы байланыс.

5. Денелерді өзектер (стерженьдер) арқылы байланыстыру. Өзектік байланыстар дененің өзек бойындағы екі бағыттағы қозғалысын шектейді және реакция күштері өзек бойымен бағытталады. Реакция күштерінің бағыттарына байланысты өзек созылуға немесе сығылуға қарсы жұмыс істейді.

4.5-сурет. Өзек арқылы байланыс.

6. Қатаң бекініс. Арқалық өзінің бір ұшымен қабырғаға қазықша қадалып бекітілген. Бұл бекітуді қатаң бекініс деп атаймыз. Егер осы арқалыққа белсенді күштер әсер етсе реакция күшімен бірге А нүктесінде теңгеретін шамасы белгісіз моменті қос күш пайда болады.

4.6-сурет. Қатаң бекітілген арқалықтың реакция күштері.

5-тақырып. Арқалық жүйелері. Жүктеме класификациясы. Тіректің түрлері.

Арқалық деп ұзындығы биіктігінен әлдеқайда үлкен болатын, бекіністермен бекітілген, иілуге жұмыс істейтін сырықты (брус) айтамыз.

Арқалықтар машина жасауда, құрылыста, кеме жасауда, авиацияда және тағы басқа салаларда қолданылады. Олар жиі қолданылатын конструкциялардың негізгі элементтері болғандықтан арқалықтарды есептеу маңызды әрі жауапты мәселе болып табылады.

Арқалықтар ағаштың және темірлердің түрлерінен және композиттік материалдардан жасалуы мүмкін. Арқалықты бойлық оське перпендикуляр бағытта қиып алсақ ол көлденең қима болып табылады.

Келесі көлденең қималардағы арқалықтар кеңінен таралған:

5.1-сурет. Көлденең қималардың түрлері.

Арқалықтарды қатаң бекініс арқылы, жылжымайтын топсалы бекініс арқылы және жылжымалы топсалы бекіністер арқылы бекітуге болады. Ол байланыстардың әсерін қандай реакция күштерімен алмастыру керек екендігі төртінші тақырыпта көрсетілген болатын.

Егер жүктемені бір нүктеге әсер етеді деп қабылдауға болатын болса, ондай жүктеме шоғырланған жүктеме деп аталады. Егер жүктеме белгілі бір ауданға немесе белгілі бір ұзындыққа әсер ететін болса ондай жүктемені таралған жүктеме деп атаймыз.

5.2-сурет. Жүктемелердің түрлері.

Есеп шығару кезінде таралған жүктемені формуласы арқылы шоғырланған жүктемеге келтіреміз, мұнда q-таралған жүктеменің қарқындылығы, 𝑙-жүктеменің таралу ұзындығы. Келтірілген Q шоғырланған жүктемені таралған жүктеменің дәл ортасына саламыз.

Кез-келген статикалық анықталған арқалықтың байланыс реакцияларын мына алгоритм бойынша анықтауға болады:

1. Арқалықты байланыстардан босатып байланыстар әсерін сәйкес реакция күштерімен алмастырамыз.

2. Координаталар жүйесін қабылдап аламыз.

3. Егер таралған жүктеме әсер етсе, шоғырланған жүктемеге келтіреміз.

4. Шоғырланған күштерді және шоғырланған қос күш моменттерін орындарына саламыз.

5. Тепе-теңдік теңдеулерін құрамыз:

; 2) 0; 3) .

Осы тепе-теңдік теңдеулерінің шешімі, байланыс реакцияларының мәндері болып табылады.

Егер, жазықтықта белгісіз реакциялар саны үшеуден артық болса, ондай арқалық статикалық анықталмаған арқалық деп аталады.

6-тақырып. Ауырлық центр. Кейбір фигуралардың ауырлық центрларының орыны.

Дененің жерге тартылу күшін дененің ауырлық күші деп, ал сол ауырлық күшінің түсу нүктесін дененің ауырлық ценрті деп атаймыз.

Егер, дене бірнеше күрделі бөлшектерден тұратын болса, онда денені ойша элементар бөлшектерге бөліп қарастырамыз, оның әрбір бөлшегіне вертикаль төмен бағытталатын және бөлшектің центріне түсірілетін ауырлық күштері әсер етеді. Дене өлшемдері жер радиусынан әлдеқайда аз болғандықтан, дене бөлшектеріне әсер ететін ауырлық күштерін тұрақты және біріңғай параллель бағытталған күш деп есептейміз.

Бөлшектердің ауырлық күштерінің тең әсер етуші күші дененің ауырлық күші, ал осы параллель күштер жүйесінің С центрі дененің ауырлық центрі деп аталады.

Денені кез-келген бағытта бұрғаннан дене бөлшектерінің ауырлық күштері түсірілген нүктелер орнын өзгертпейді. Сондықтан денені кез-келген бағытта бұрғанннан дененің ауырлық центрінің орны өзгермейді. Дененің ауырлық центрінің орынын анықтау үшін параллель күштер жүйесінің центрін анықтайтын теңдіктерді қолданамыз.

Дененің С центрінің Охуz координаталар жүйесіне қатысты координаталарын 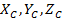деп белгілесек:

мұнда, дене бөлшектерінің ауырлық центрінің түсу нүктелерінің орыны.

, , дененің хуz координаталарына қатысты статикалық моменттері деп аталады.

Егер, хуz координаталар жүйесі дененің ауырлық центрі арқылы өтетін болса, онда статикалық моменттер нольге тең болады, себебі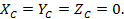

Егер дене қалыңдығы тұрақты біртекті жазық жұқа фигура арқылы берілсе, она дене бөлшектерінің салмағы бет ауданына, ал фигураның Р салмағы жалпы S ауданына тәуелді болады. µ∙ және 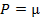∙S(мұнда фигураның бірлік ауданының салмағы, өлшем бірілігі ). Ендеше, жазық фигура үшін, жоғарыдағы формулада дененің ауырлық күшінің орнына, дененің ауданын қолдануға болады.

Жазық біртекті фигураның жоғарыдағы формулалар негізінде ауырлық центрінің координаталары былайша анықталады:

Тіктөртбұрыш ауданының ауырлықцентрі оның диоганальдарының қиылысу нүктесінде орналасады, ал оның ауырлық центрынан кез-келген қабырғасына түсірілген перпендикуляр қабырғаны екіге бөледі.

Үшбұрыш ауданының ауырлықцентрі оның медианаларының қиылысу нүктесінде орналасады, ал ауырлық центрдан кез-келген табанына түсірілген перпендикулярдың ұзындығы үшбұрыштың биіктігінің 1/3 бөлігіне тең болады.

6.1-сурет. Тіктөртбұрыштың және үшбұрыштың ауырлық центрі.

Поиск по сайту: