 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН. Центром паралельних сил називається точка на лінії дії рівнодійної цих сил, яка не змінює свого положення при повороті всіх сил навколо точок їх прикладення
Центром паралельних сил називається точка на лінії дії рівнодійної 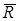 цих сил, яка не змінює свого положення при повороті всіх сил навколо точок їх прикладення
цих сил, яка не змінює свого положення при повороті всіх сил навколо точок їх прикладення 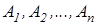 на один і той самий кут в одному напрямку, наприклад
на один і той самий кут в одному напрямку, наприклад 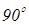 (рис. 3.20).
(рис. 3.20).
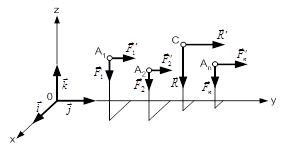 Рис. 3.20
Рис. 3.20
| Якщо головний вектор системи паралельних сил 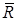 не дорівнює нулю, то існує центр паралельних сил (точка не дорівнює нулю, то існує центр паралельних сил (точка  ), який визначається за формулою ), який визначається за формулою  , ,
|
або в проекціях на координатні осі:
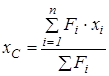 ;
; 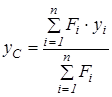 ;
; 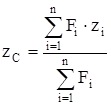 ,
,
де 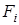 - модуль її сили;
- модуль її сили; 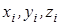 - координати її точки прикладення.
- координати її точки прикладення.
Положення центра паралельних сил не залежить від напряму сил, а залежить тільки від їхніх модулів і їхніх точок прикладення.
Центром ваги тіла  називається центр паралельних сил ваги його елементарних частин (рис. 3.21). Якщо тіло можна поділити на деяку кількість частин, в яких положення центра ваги відоме, то координати центра ваги тіла будуть:
називається центр паралельних сил ваги його елементарних частин (рис. 3.21). Якщо тіло можна поділити на деяку кількість частин, в яких положення центра ваги відоме, то координати центра ваги тіла будуть:
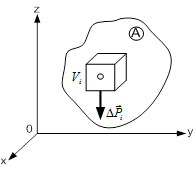 Рис. 3.21
Рис. 3.21
| 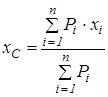 ; ;  ; ; 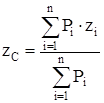 , ,
|
де  - вага окремої частини;
- вага окремої частини; 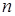 - кількість частин;
- кількість частин; 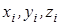 - координати центра ваги окремої частини.
- координати центра ваги окремої частини.
Ці вирази визначають центр ваги неоднорідного тіла.
Центр ваги однорідного твердого тіла (або центр об’єму тіла) визначається за формулами
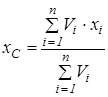 ;
; 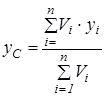 ;
;  ,
,
де 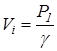 ,
, 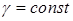 - щільність, вага одиниці об’єму.
- щільність, вага одиниці об’єму.
Чисельники мають назву статичних моментів об’єму відносно координатних площин  . У разі, якщо паралельні сили неперервно розподілені по деякій однорідній (
. У разі, якщо паралельні сили неперервно розподілені по деякій однорідній (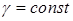 ) площині
) площині 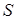 , то вага частини
, то вага частини  пропорційна їх площам
пропорційна їх площам  (рис. 3.22).
(рис. 3.22).
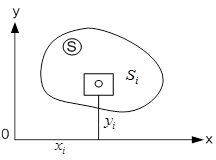 Рис. 3.22
Рис. 3.22
| У цьому випадку координати центра ваги площини визначаються за формулами
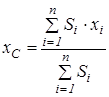 ; ; 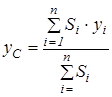 . .
|
Вирази 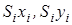 називаються статичними моментами площі плоскої фігури відносно координатних осей
називаються статичними моментами площі плоскої фігури відносно координатних осей 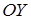 і
і 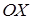 (рис. 3.22).
(рис. 3.22).
Центр ваги лінії.
Якщо однорідне тіло має форму тонкого криволінійного стержня з постійною площею 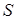 поперечного перерізу, то вага частини
поперечного перерізу, то вага частини  пропорційна її довжині
пропорційна її довжині 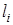 . Тоді координати центра ваги стержня визначаються формулами
. Тоді координати центра ваги стержня визначаються формулами
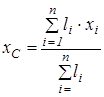 ;
; 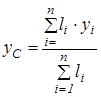 ;
;  .
.
Чисельники є статичними моментами лінії відносно координатних площин  .
.
Методи визначення координат центра ваги однорідних тіл
1) Метод симетрії – якщо тіло має площину, вісь або центр симетрії, то його центр ваги лежить відповідно у площині, на осі або в центрі симетрії.
Приклади:
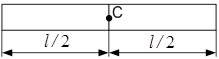 а а
| а) стержень: центр ваги  розташований у середині стержня (рис. 3.23,a); розташований у середині стержня (рис. 3.23,a);
|
 б б
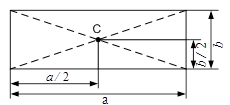
| б) прямокутник: центр ваги  - точка перетину діагоналей прямокутника (рис.3.23,б); - точка перетину діагоналей прямокутника (рис.3.23,б);
|
 c c
| c) трикутник (рис. 3.23,с): центр ваги  - точка перетину медіан трикутника - точка перетину медіан трикутника  , , 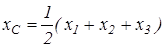 де де  - координати точок - координати точок 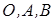 . Площа . Площа 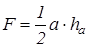 ; ;
|
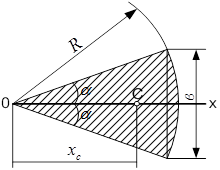 d d
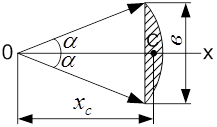
| d) коловий сектор (рис. 3.23,d): центр ваги  лежить на бісектрисі сектора і його відстань від центра сектора лежить на бісектрисі сектора і його відстань від центра сектора 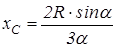 . Площа . Площа 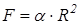 , тому , тому 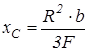 .
Півколо ( .
Півколо (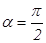 ). Площа ). Площа 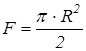 , координата точки , координата точки   ; ;
|
 k
Рис. 3.23 k
Рис. 3.23
| k) коловий сегмент (рис. 3.23,k). Площа 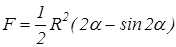 . Координата точки . Координата точки  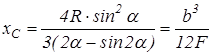 ,
де кут ,
де кут 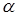 має бути виражений у радіанах. має бути виражений у радіанах.
|
2) Метод розбивання. Якщо тіло (або площину) можна розбити на скінчене число елементарний фігур, в яких положення центра ваги відоме, то координати центра ваги визначаються формулами, доведеними вище.
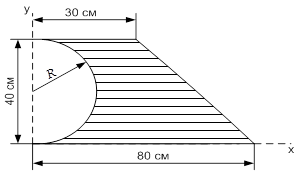
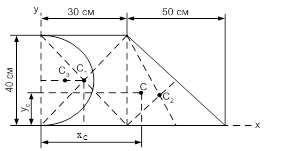
Приклад. Визначити координати центра ваги площі фігури (рис. 3.24,а).
 а а
| Розв’язання. Розіб’ємо фігуру на три елементарні фігури, для яких відомі центри ваги, та легко визначаються площі: прямокутник, трикутник і півколо (рис. 3.24,б). Площу півкола, вирізану з прямокутника, вважаємо тілом з від’ємною площиною.
Координати центра ваги плоскої фігури визначаємо за формулами
 ; ; 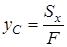 , ,
|
 б
Рис. 3.24 б
Рис. 3.24
|
де 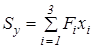 ,
, 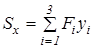 - статичні моменти фігури відносно координатних осей
- статичні моменти фігури відносно координатних осей 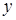 і
і 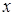 ,
,  - площа фігури.
- площа фігури.
Дані про площі елементарних фігур (прямокутника, трикутника та півкола), координати їхніх центрів ваги, статичних моментів відносно координатних осей запишемо в таблиці.
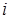
| 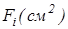
| 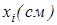
| 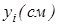
| 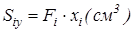
| 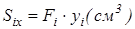
|
| 15,0 | 20,0 | ||||
| 46,7 | 13,3 | ||||
| -628 | 8,5 | 20,0 | -5338 | -12500 | |
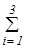
| ‑ | ‑ |
Координати центра ваги всієї фігури:
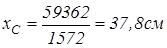 ;
;
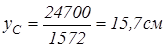 .
.
Центр ваги  площі всієї фігури показуємо на рисунку.
площі всієї фігури показуємо на рисунку.
Запитання для самоконтролю
1. Які властивості має центр паралельних сил?
2. За якими формулами визначаються координати центра паралельних сил?
3. За якими формулами визначаються координати центра ваги тіла?
4. Що називають статичним моментом площі плоскої фігури відносно осі?
5. За якими формулами визначаються центри ваги плоскої фігури?
6. Як визначити положення центра ваги плоскої фігури з отворами?
3.10. Завдання для контрольних робіт з розділу “Статика”
Завдання для роботи “Визначення реакцій опор складеної конструкції”
Конструкція складається з двох тіл. Визначити реакції А і В, а також тиск у проміжному шарі С. Схеми конструкцій наведені на рис. 3.25 – 3.27. Необхідні для розрахунків дані наведені в таблиці.
| Номер варіанта | 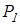
| 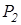
| М, кН 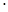 м м
| q, кН/м |
| кН | ||||
| 5,0 | - | 24,0 | 0,8 | |
| 6,0 | 10,0 | 22,0 | 1,0 | |
| 7,0 | 9,0 | 20,0 | 1,2 | |
| 8,0 | - | 18,0 | 1,4 | |
| 9,0 | - | 16,0 | 1,6 | |
| 10,0 | 8,0 | 25,0 | 1,8 | |
| 11,0 | 7,0 | 20,0 | 2,0 | |
| 12,0 | 6,0 | 15,0 | 2,2 | |
| 13,0 | - | 10,0 | 2,4 | |
| 14,0 | - | 12,0 | 2,6 | |
| 15,0 | 5,0 | 14,0 | 2,8 | |
| 12,0 | 4,0 | 16,0 | 3,0 | |
| 9,0 | 6,0 | 18,0 | 3,2 | |
| 6,0 | - | 20,0 | 3,4 | |
| 5,0 | 8,0 | 22,0 | 3,6 | |
| 7,0 | 10,0 | 14,0 | 3,8 | |
| 9,0 | 12,0 | 26,0 | 4,0 | |
| 11,0 | 10,0 | 18,0 | 3,5 | |
| 13,0 | 9,0 | 30,0 | 3,0 | |
| 15,0 | 8,0 | 25,0 | 2,5 | |
| 10,0 | 7,0 | 20,0 | 2,0 | |
| 5,0 | 6,0 | 15,0 | 1,5 | |
| 8,0 | 5,0 | 10,0 | 1,4 | |
| 11,0 | 4,0 | 5,0 | 1,3 | |
| 14,0 | 6,0 | 7,0 | 1,2 | |
| 12,0 | 8,0 | 9,0 | 1,1 | |
| 10,0 | 7,0 | 11,0 | 1,0 | |
| 8,0 | 9,0 | 13,0 | 1,2 | |
| 5,0 | 7,0 | 10,0 | 1,5 | |
| 10,0 | 12,0 | 17,0 | 1,6 |

Рис. 3.25
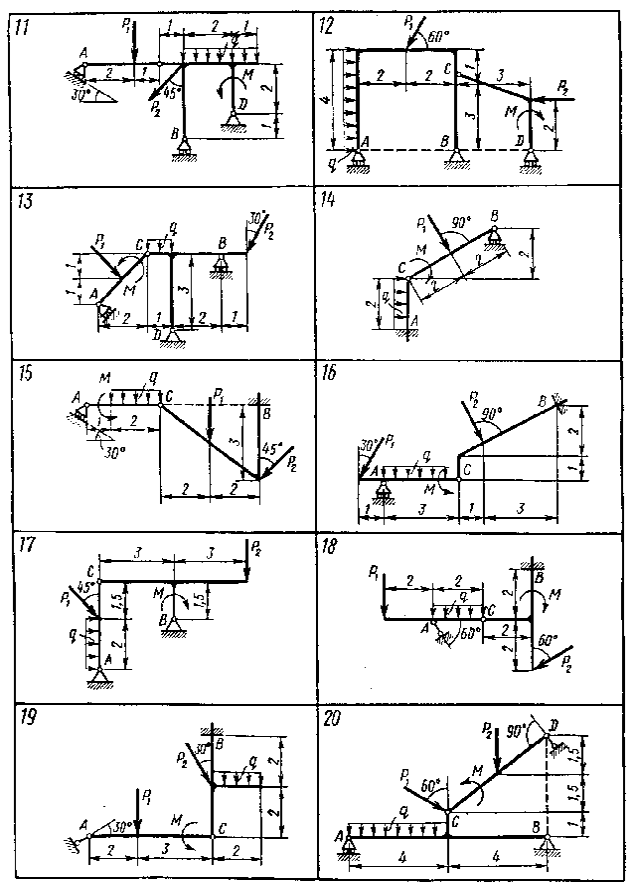
Рис. 3.26
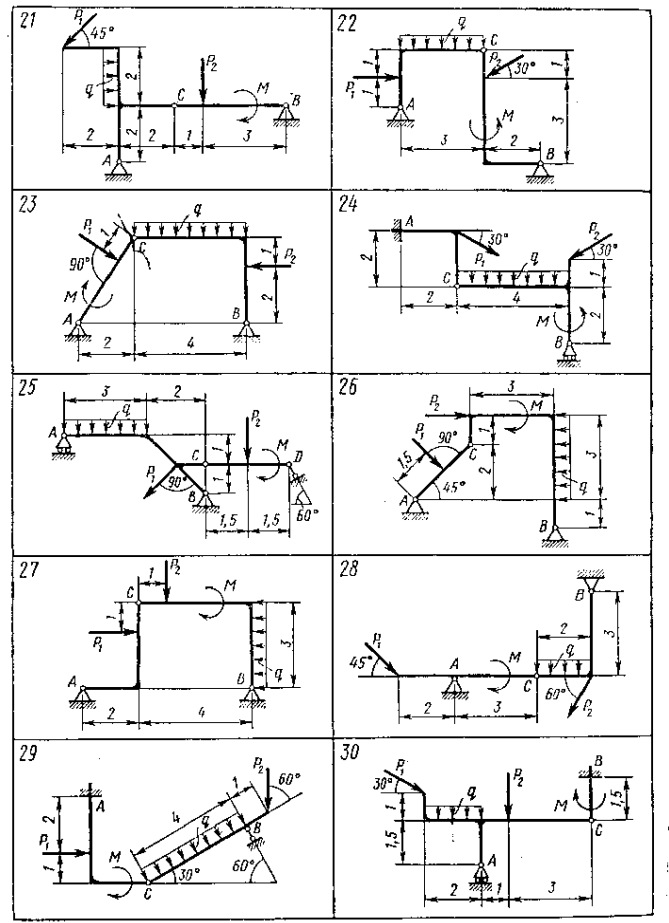
Рис. 3.27
Завдання для роботи “Визначення реакцій опор твердого тіла”
Визначити реакції опор конструкції. Схеми конструкції наведені на рис. 3,28-3,30. Значення зовнішніх сил Q, T, G, а також розміри а, b, c, R, r наведені нижче.
| Номер варіанта | Сили, кН | Розміри, см | ||||||
| Q | T | G | a | b | c | R | r | |
| - | ||||||||
| - | ||||||||
| - | - | - | ||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | - | - | - | |||||
| - | ||||||||
| - | - | - | ||||||
| - | ||||||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | - | - | |||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | - | |||||
| - | - | - | ||||||
| - | ||||||||
| - | - | - | - |
Примітка.
1. Вважати, що у варіантах 18, 22-26 петлі не заважають переміщенню рами уздовж АВ.
2. У варіантах 20 і 21 поверхні, які торкаються, вважати абсолютно гладенькими.
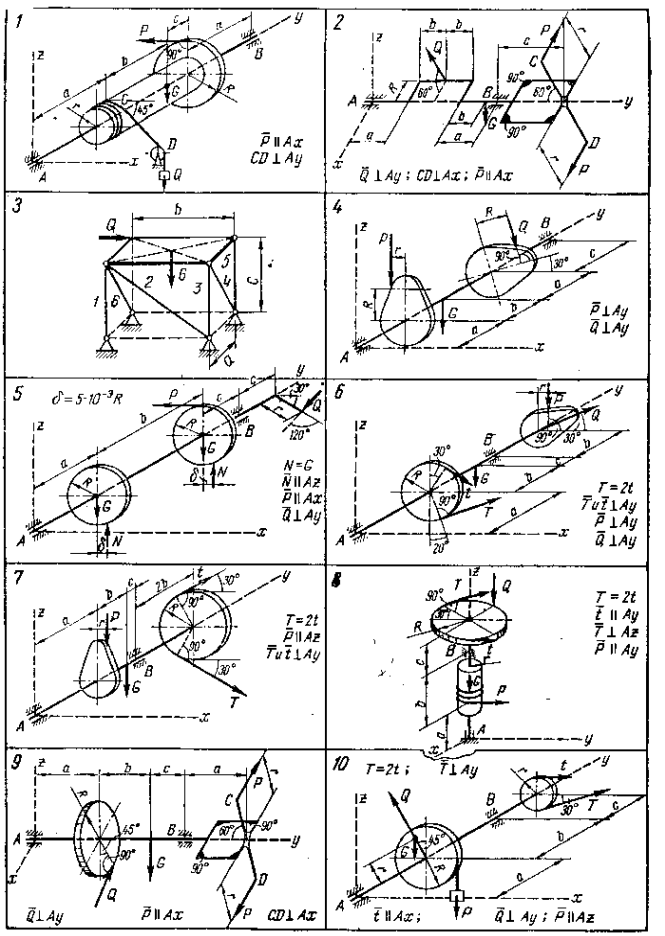 Рис. 3.28
Рис. 3.28
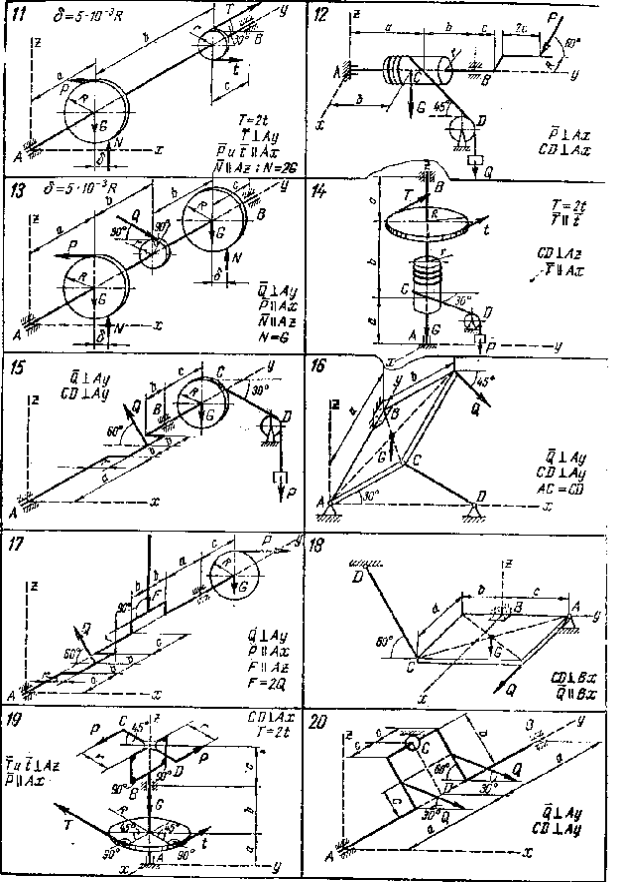
Рис. 3. 29
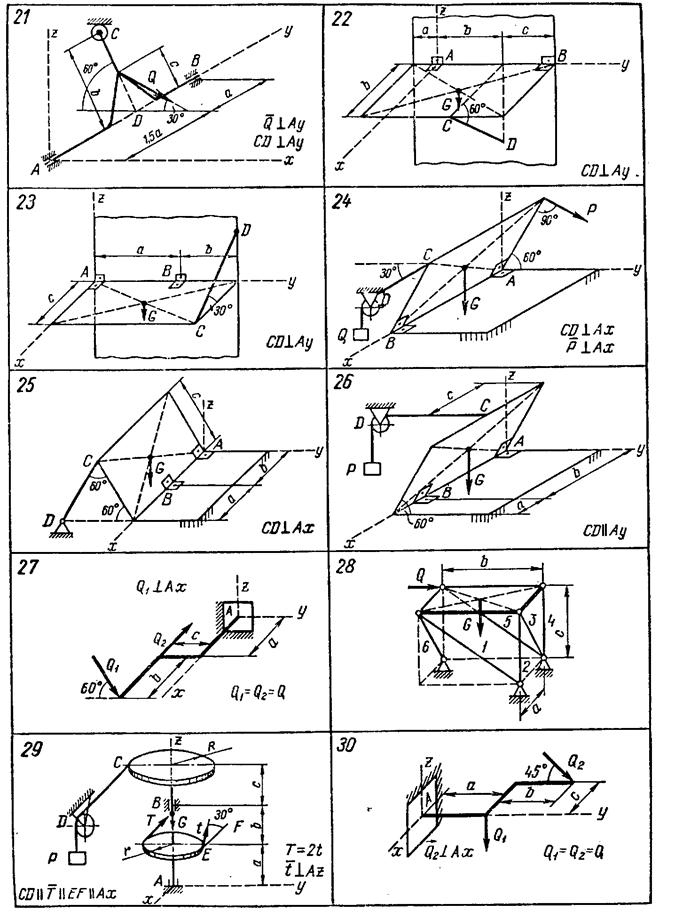
Рис. 3.30
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
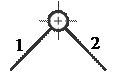
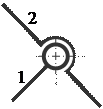
 1. С помощью какой схемы кинематической пары можно осуществить три вращательных движения одного звена относительно другого
1. С помощью какой схемы кинематической пары можно осуществить три вращательных движения одного звена относительно другого
A)
 |
B)
 |
C)
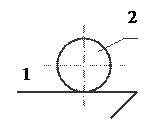 |
D)
 |
E)
 2. С помощью какой схемы кинематической пары можно осуществить три поступательных движения одного звена относительно другого
2. С помощью какой схемы кинематической пары можно осуществить три поступательных движения одного звена относительно другого
A)
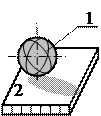 |
B)
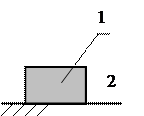 C)
C)
 |
D)
 |
E)
3. С помощью какой пары можно осуществить только вращательное движение первого звена относительно другого
 |
A)
 |
B)
 |
C)
 |
D)
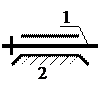 |
E)
4. С помощью какой кинематической пары можно осуществить только возвратно-поступательное движение одного звена относительно другого
 |
A)
 |
B)
 |
C)
 D)
D)
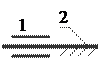 E)
E)
5. С помощью какой пары можно осуществить вращательное и поступательное движение одного звена относительно другого
 |
A)
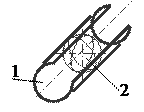 B)
B)
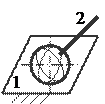 |
C)
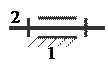
D)
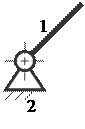
E)
6. Как можно кинематическую пару с тремя степенями свободы превратить в кинематическую пару с двумя степенями
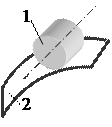 |
A)
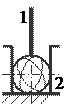 |
B)

C)
 |
D)
 |
E)
7. С помощью какой схемы пары можно осуществить зависимое поступательное перемещение звена при вращении его относительно другого
 |
A)
 B)
B)
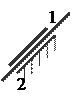 |
C)
 |
D)
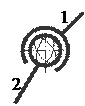 |
E)
8. Определите степень свободы плоского механизма.
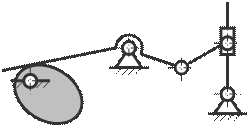 A) 1
A) 1
B) 2
C) 3
D) 4
E) 5
9. Укажите на схеме кинематические пары 3 класса (Р3)
 A) 5
A) 5
B) 1
C) 3
D) 4
Е) 2
10. Сколькими степенями свободы обладает цирковое шаровое колесо относительно гладкого пола арены?
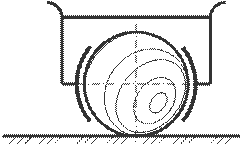 A) 4
A) 4
B) 2
C) 3
D) 5
E) 1
11. Механизм Витворта это
A) тангенсный механизм
B) двухкулисный механизм
C) двухкоромысловый механизм
D) синусный механизм
E) кулисный механизм
12. Определите степень свободы механизма строгального станка.
 A) 1
A) 1
B) 2
C) 3
D) 4
E) 5
13. Определите степень свободы механизма вытяжного пресса.
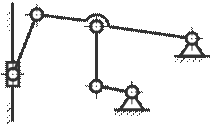 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
14. Определите степень свободы механизма долбёжного станка.
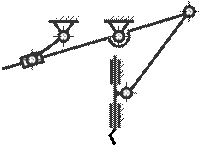 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
15. Определите степень свободы механизма качающегося конвейера.
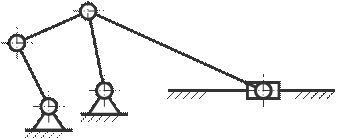 A) 5
A) 5
B) 2
C) 3
D) 4
E) 1
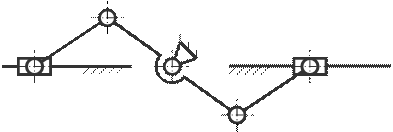 16. Определите степень свободы механизма поршневого компрессора для двухступенчатого сжатия воздуха.
16. Определите степень свободы механизма поршневого компрессора для двухступенчатого сжатия воздуха.
A) 3
B) 2
C) 1
D) 4
E) 5
17. Определите степень свободы механизма Дизеля (R.Diesel).
 A) 5
A) 5
B) 2
C) 3
D) 4
E) 1
18. Определите степень свободы механизма манипулятора.
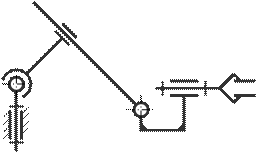 A) 5
A) 5
B) 7
C) 6
D) 8
E) 9
19. Определите степень свободы механизма манипулятора.
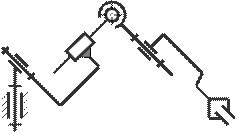 A) 9
A) 9
B) 6
C) 8
D) 5
E) 7
20. Определите степень свободы механизма манипулятора.
 A) 6
A) 6
B) 5
C) 3
D) 2
E) 1
21. Определите степень свободы синусного механизма.
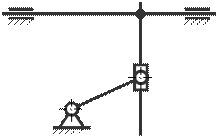 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
22. Определите степень свободы механизма колодочного тормоза.
A) 5
 B) 2
B) 2
C) 3
D) 4
E) 1
23. Укажите на схеме кинематические пары 4 класса (Р4)
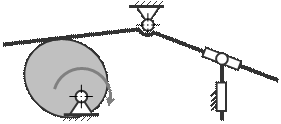 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
24. Укажите на схеме кинематические пары 4 класса (Р4)
A) 3
 B) 2
B) 2
C) 1
D) 4
E) 5
25. Механизм муфты Ольдхема (Oldham) это
A) двухкулисный механизм
B) кривошипно-ползунный механизм
C) двухкоромысловый механизм
D) синусный механизм
E) тангенсный механизм
26. Определить степень подвижности механизма Робертса
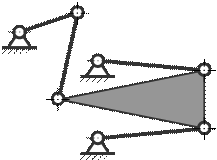 A) 2
A) 2
B) 1
C) 3
D) 4
E) 5
27. Определить степень подвижности муфты Ольдхема (Oldham)
 A) 3
A) 3
B) 2
C) 1
D) 4
E) 5
28. Определите степень подвижности плоского механизма
 A) 2
A) 2
B) 1
C) 3
D) 4
E) 5
29. Определите степень подвижности механизма конхоидографа
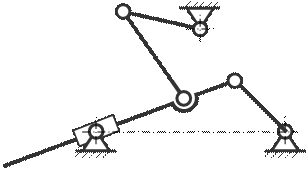 A) 5
A) 5
B) 2
C) 3
D) 4
E) 1
30. Определите степень подвижности кулачкового механизма
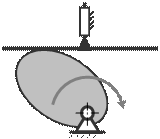 A) 3
A) 3
B) 2
C) 1
D) 4
E) 5
31. Определите степень подвижности плоского механизма
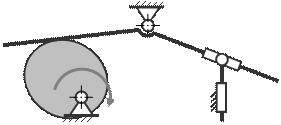 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
32. Определите степень подвижности плоского механизма
 A) 1
A) 1
B) 2
C) 3
D) 4
E) 5
33. Определите степень подвижности кулачкового механизма
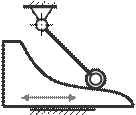 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
34. Определите степень подвижности пространственного механизма
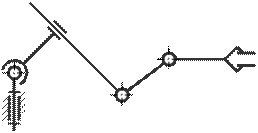 A) 3
A) 3
B) 6
C) 8
D) 4
E) 5
35. Определите степень подвижности плоского механизма
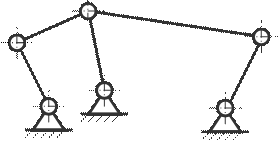 A) 1
A) 1
B) 2
C) 3
D) 4
E) 5
36. Определите степень подвижности плоского механизма
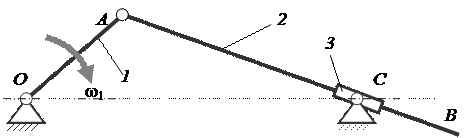 A) 4
A) 4
B) 2
C) 3
D) 1
E) 5
37. Определите класс механизма.
 A) I – класс
A) I – класс
B) II – класс
C) III – класс
D) IV – класс
E) V – класс
38. Определите класс механизма.
 A) III – класс
A) III – класс
B) II – класс
C) I – класс
D) IV – класс
E) V – класс
39. Определите класс механизма.
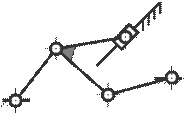 A) I – класс
A) I – класс
B) II – класс
C) III – класс
D) IV – класс
E) V – класс
 40. Определите класс механизма.
40. Определите класс механизма.
A) IV – класс
B) I – класс
C) III – класс
D) II – класс
E) V – класс
41. Определите класс механизма.
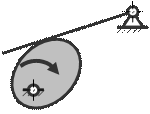 A) V – класс
A) V – класс
B) I – класс
C) III – класс
D) IV – класс
E) II – класс
42. Определите класс механизма.
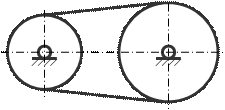 A) II – класс
A) II – класс
B) I – класс
C) III – класс
D) IV – класс
E) V – класс
43. Определите класс механизма.
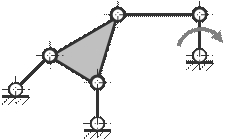 A) II – класс
A) II – класс
B) I – класс
C) III – класс
D) IV – класс
E) V – класс
44. Определите класс механизма.
 A) I – класс
A) I – класс
B) IV – класс
C) III – класс
D) II – класс
E) V – класс
45. Определите класс механизма.
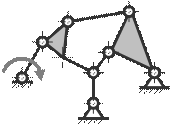 A) III – класс
A) III – класс
B) I – класс
C) V – класс
D) IV – класс
E) II – класс
46. Определите структурную формулу для анализа плоских механизмов
A) W = 6 n – 5 p5 – 4 p4 – 3 p3 – 2 p2 – p1
B) W = 3 n – 2 p5 – 3 p3 – p4
C) W = 3 n – 3 p3 – 2 p2 – p4
D) W = 6 n – 4 p4 – 2 p5 – p1
E) W = 3 n – 2 p5 – p4
47. Определите структурную формулу для анализа пространственных механизмов
A) W = 6 n – 3 p 3 – 4 p 4 – 2 p 2
B) W = 6 n – 5 p 5 – 4 p 4 – 3 p 3 –2 p 2 – p 1
C) W = 6 n – 2 p 2 – p 4
D) W = 3 n – 2 p 5 – p 4
E) W = 6 n – 5 p 4 – 4 p 5 – 3 p 3
48. Определите класс кинематической пары, образованной звеньями 1 и 2.
 A) II
A) II
B) I
C) III
D) IV
E) V
49. Механизм включает в себя одну группу Ассура второго класса. Какого вида эта группа
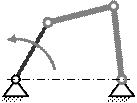 A) четвёртого вида
A) четвёртого вида
B) второго вида
C) третьего вида
D) первого вида
E) пятого вида
50. Определите класс кинематической пары, образованной звеньями 1 и 2.
A) IV
 B) II
B) II
C) III
D) I
E) V
51. Механизм включает в себя одну группу Ассура второго класса. Какого вида эта группа
A) четвёртого вида
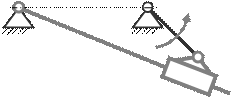 B) второго вида
B) второго вида
C) первого вида
D) третьего вида
E) пятого вида
52. Определите класс кинематической пары, образованной звеньями
 A) III
A) III
B) II
C) I
D) IV
E) V
53. Механизм включает в себя одну группу Ассура второго класса. Какого вида эта группа
 A) пятого вида
A) пятого вида
B) первого вида
C) третьего вида
D) четвёртого вида
E) второго вида
54. Определите класс кинематической пары, образованной звеньями 1 и 2.
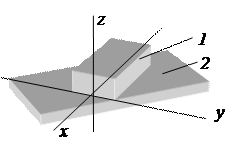 A) IV
A) IV
B) II
C) I
D) III
E) V
55. Механизм включает в себя одну группу Ассура второго класса. Какого вида эта группа
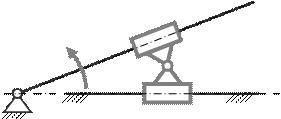 A) четвёртого вида;
A) четвёртого вида;
B) второго вида;
C) третьего вида;
D) первого вида;
E) пятого вида.
56. Определите класс кинематической пары, образованной звеньями
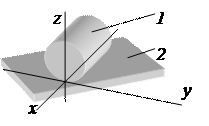 A) III
A) III
B) I
C) II
D) IV
E) V
57. Механизм включает в себя одну группу Ассура второго класса. Какого вида эта группа?
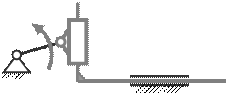 A) четвёртого вида
A) четвёртого вида
B) второго вида
C) третьего вида
D) пятого вида
E) первого вида
58. Что происходит за время выбега машины?
А) Накопление кинетической энергии
В) Поглощение кинетической энергии
Поиск по сайту: