Работа. Механическая энергия. Кинетическая и потенциальная энергия. Закон сохранения механической энергии

Если на теле действует постоянная сила F и тело в направлении действия силы соверша­ет перемещение s, то говорят, что сила со­вершает работу А, равную произведению мо­дулей векторов силы и перемещения на коси­нус угла между этими векторам, (рис. 7.1): A = Fs cos α.

Единица измерения силы — джоуль (Дж). Работа равна 1 Дж, если она совершена силой 1 Н на пути в 1 м: 1Дж = 1Н1м.

Работа — величина скалярная, т.е. не имеет направления. Если на тело действуют несколько сил, то под F подразуме­вается результирующая всех сил. Если сумма всех сил равна 0, значит, равна 0 и суммарная работа всех сил, хотя каждая действующая сила совершает работу, если тело перемещает­ся в пространстве. В этом случае работа одних сил положи­тельна, а других отрицательна. Положительной считается работа сил, которые сонаправлены с перемещением, отрица­тельной, если работа сил противоположна перемещению.

Например, при подъеме груза работа силы натяжения положительна, а ра­бота силы тяжести — отрицательна (рис. 7.2).

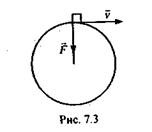
Если направление действия силы перпендикулярно перемещению, то и работа этой силы равна 0 (cos90° = 0). Например, не совершает работы сила, которая заставляет тело двигаться по окружности, рис. 7.3.

Рассмотрим работу силы тяжести (рис. 7.4). Пусть тело массой т сво­бодно падает с высоты h1 до высоты h2 относительно выбранного нулево­го уровня. Направление перемещения и действия силы тяжести F = mg совпадают, следовательно, работа силы тяжести равна A = mg(h1-h2).

Если тело брошено вверх, то работа силы тяжести будет отрицательная A = -mg(h1-h2). При движении тела по наклонной плоскости работа силы тяжести равна А = mgscosa, где a - это угол между вектором силы и вектором перемещения. Но scos a = h, следовательно, работа равна А = mgh.

Если тело движется по некоторой произвольной траектории, то ее мож­но разбить на множество наклонных плоскостей. Полная работа на всем пути равна А = mgh1 + mgh2 +…,

где h— общая высота подъема, т.е. А = mgh.

Значит, работа силы тяжести не зависит от формы траектории движения тела. Работа силы тяжести равна произведению силы тяжести на разность высот в начальном и конечном положениях. Если тело движется вверх, то работа отрицательна, при движении вниз работа положительна. Работа си­лы тяжести на замкнутой траектории равна 0, так как происходит алгебраи­ческое сложение равных величин с разными знаками.

Величину mgh называют потенциальной энергией тела. Выражение для работы силы тяжести можно переписать

A = -mg(h2-hl).

Работа силы тяжести равна изменению потенциальной энергии тела, взятой с противоположным знаком. Знак минус означает следующее. Если работа силы тяжести положительна, то потенциальная энергия тела умень­шается (при падении потенциальная энергия тела уменьшается). Потенци­альной энергией обладают и покоящиеся тела, так как от скорости потенци­альная энергия не зависит, а зависит только от положения тела относитель­но выбранного нулевого уровня. Однако работа, которая совершается при перемещении тела, от выбранного потенциального уровня не зависит, так как она равна изменению потенциальной энергии.

Для вычисления работы силы упругости надо среднее значение этой ве­личины умножить на перемещение, так как силы упругости при движении изменяются, поскольку изменяется удлинение пружины: А= Fср(x1 – x2).

Среднее значение силы упругости находят из определения средней величины в математике F= (кх1 + кх2)/2=к(х1+х2)/2. Подставим среднее значе­ние силы упругости в выражение для работы и получим А= кx1/2 – кх2/2.

Работа силы упругости зависит от координат начального и конечного положений тела. Величину кхг/2- называют потенциальной энергией деформированного тела. Работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным зна­ком: А=(кх22 /2 – кх21/2).

Работа силы упругости не зависит от формы траектории, а если траек­тория замкнута, то работа равна 0. Способность тела совершать механиче­скую работу характеризует физическая величина, которая получила назва­ние механической энергии. Полная механическая энергия складывается из кинетической и потенциальной энергии. Кинетической энергией обладают все движущиеся тела.

Если на тело действует сила F и тело совершает перемещение s, то работа данной силы А = F s cos a, cos а = 1. |

Согласно второму закону Ньютона, F = та. Подставим это выражение в формулу работы, получим А = mv22/2 - mv21/2 Величину mv2/2 называют кинетической энергией тела Ек. Энергия (так же как и импульс) имеет свойство сохраняться. Рассмотрим замкнутую систему тел, т.е. систему, где тела взаимодействуют только друг с другом. Тела в такой системе могут обладать и потенциальной энергией, и кинетической. Изменение потенциальной энергии тела, взятой со знаком минус, равно изменению кинетиче­ской энергии системы, т.е. совершенная работа силами тяжести и упругости записывается

А = -(Ер2-Ер1), но эта же работа равна А =(Ер2 – Ер1). Отсюда видно, что при возраста­нии одной энергии другая уменьшается, т.е. происходит превращение одно­го вида энергии в другой. Сумму кинетической и потенциальной энергии называют полной механической энергией. Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной. Это формулировка закона сохранения энергии. Закон сохранения механической энергии справедлив при отсутст­вии сил трения, т.е. в системе не происходит перехода механической энер­гии в другие виды энергии. Законы сохранения позволяют по начальному состоянию системы определить ее конечное состояние, не выясняя величи­ны сил взаимодействия. При рассмотрении работы силы трения надо ис­пользовать закон сохранения полной энергии.

2. Качественная задача по разделу «Мо­лекулярная физика»

На рис. 7,5 представлен график изменения давления в зависимости от температуры для не­которой массы идеального газа. Как при этом изменялся объем газа?

Соединим начало координат с несколькими точками на графике. Проведенные прямые явля­ются изохорами. Выделим прямую 1-2. Очевид­но, что при температуре Т2 объем V2 больше, чем V1 т.е. объем газа в этом процессе увеличивался.

.

3. Текст по разделу «Электродинамика», содержащий описание использования законов электродинамики в технике. Задание на понимание основных принципов, лежащих в основе работы опи­санного устройства

Какое хочу, такое и получу

При практическом использовании энергии электрического тока очень часто возникает необходимость изменять напряжение, даваемое каким-либо генератором. В одних случаях нужны напряжения в тысячи или даже сотни тысяч вольт, в других необходимы напряжения в несколько вольт или несколько десятков вольт. Осуществить такого рода преобразова­ния можно в устройствах, которые называют трансформаторами. В основе работы транс­форматора лежит явление электромагнитной индукции. Трансформатор состоит из двух обмоток, надетых на магнитомягкий стальной сердечник. Сердечник собран из пластин. Одна из обмоток, называемая первичной, подключа­ется к источнику переменного тока. Вторая обмотка, к которой подсоединяют «нагрузку»,называют вторичной (рис. 7.6).

Для трансформаторов, работающих на холостом ходу, справедливо со­отношение

U1/U2= N1/N2= к, где U1, U2 — напряжения на первичной и вторичной обмотках трансфор­матора, a N1 и N2 — число витков на первичной и вторичной обмотках трансформатора. Величину к называют коэффициентом трансформации. Трансформатор преобразует переменный электрический ток таким образом, что произведение силы тока на напряжение приблизительно одинаково в первичной и вторичной обмотках.

Электрическая энергия — самая универсальная и удобная форма энер­гии для передачи на большие расстояния. Удвоение потребления электроэнергии происходит в среднем за 10 лет. Это означает, что роль трансфор­маторов как повышающих, так и понижающих будет возрастать.

Ответьте на вопросы к тексту:

1. В чем заключается явление электромагнитной индукции?

2. Может ли трансформатор работать от постоянного тока?

3. Каковы потери передаваемой мощности в трансформаторах?

4. Почему сердечник трансформатора набирается из пластин?

БИЛЕТ № 8

1. Механические колебания. Свободные и вынужденные коле­бания. Резонанс. Превращение энергии при механических колеба­ниях

Механические колебания происходят под действием силы, пропорцио­нальной смещению и направленной ему противоположно. Такие колебания называют гармоническими.

Гармонические колебания можно рассмотреть на примере пружинного маятника. В отсутствие сил трения колебательная система является консер­вативной, поэтому для нее выполняется закон сохранения полной механи­ческой энергии:

Полная механическая энергия гармонических колебаний пропорцио­нальна квадрату их амплитуды:

2 С ростом энергии колебаний возрастает их амплитуда:

где к — жесткость пружины. Как видно из формулы, чем жестче пружина, тем меньше амплитуда колебаний. Полная механическая энергия гармони­ческих колебаний пружинного маятника сохраняется, а его кинетическая и потенциальная энергии непрерывно изменяются.

Потенциальная энергия гармонических колебаний зависит от координаты,

_ _кх2 ■Р~ 2 ' Кинетическая и потенциальная энергия маятника (рис. 8.1), согласно за­кону сохранения энергии, равна полной механической энергии:

2 " 2 2

На рис. 8.1 изображены графики зависимостей Ер (х) и ЕК (х).

Потенциальная энергия максимальна в точках поворота, когда х = ±А, и ми­нимальна в положении равновесия при х — 0. Кинетическая энергия, наоборот, минимальна в точках поворота и максимальна в положении равновесия.

Колебания, происходящие под действием внутренних сил в системе, выведенной из положения равновесия и предоставленной самой себе, назы­вают свободными.

Уравнением координаты движения маятника является уравнение

х = Acos(o0t, где со0 — циклическая частота; w0 = 2nv. Циклическая частота показывает;

число колебаний за 2л секунд.

Свободные колебания являются затухающими, т.е. амплитуда уменьша-ется с течением времени, так как в реальной системе механическое движе- I ние всегда сопровождается трением (рис. 8.2).

Силы трения, направленные противоположно перемещению маятника, совершают отрицательную работу, уменьшая его механическую энергию.

Рассмотрим характерные особенности вынужденных колебаний в сис­теме, в которой возможны собственные колебания с частотой ©0 в от­сутствие внешнего воздействия. Такой системой является, например, пружинный маятник (рис. 8.3).

Предположим, что на горизонтальный пружинный маятник массой т (жесткость пружины к) по оси X действует периодическая внешняя сила F s = F0cos <u0t. Для определенности будем считать, что в начальный момент времени пружина максимально растянута (х0 - А) и неподвижна (v о = 0), В этот момент сила упругости пружины Fynp > F x = Fa.

Если маятник отпустить, то он ускоренно начнет двигаться влево, а потом, сжимая пружину, возвратится в первоначальное положение. Затем процесс повторится. В системе возникнут вынужденные гармонические колебания с частотой со вынуждающей силы и с амплитудой А:

x=Acos со t.

Чтобы найти амплитуду вынужденных колебаний маятника, воспользу­емся вторым законом Ньютона. По оси X на маятник действуют сила упру­гости пружины F = -Ах и внешняя периодическая сила Fx, поэтому второй закон Ньютона имеет вид:

тах = -кх -г F0 cos со t. Используя выражение для ускорения при колебательном движении ах. = - со A cos со t и формулу х=Асо% со t, запишем второй закон Ньютона в виде: -mco'Acoscoi = -kAcoscot + Fucoscot. Сокращая выражение на cos со t и учитывая, что к = тсо2,. по 1) чаем вы­ражение для амплитуды вынужденных колебаний:

т(со\-сог)

Как следует из этой формулы, амплитуда вынужденных колебаний зави­сит от частоты вынуждающей силы. Для построения графика полученной зависимости рассмотрим предельные случаи малых и больших частот.

• При со = О F х = F№ т.е. на маятник действует постоянная сила, не завися­щая от времени. В этом случае х - А

тщ

Полученное соотношение определяет статическое смещение маятника.

• Если частота вынуждающей силы меньше частоты собственных колеба-

ний (со < ojq), то при увеличении частоты со0 оразность (щ — со) в знаме­нателе дроби уменьшается. Это означает, что при частоте со<со0

амплитуда вынужденных колебаний увеличивается с ростом частоты (рис. 8.4, кривая 1).

• При большой частоте со частота вынуждающей силы существенно превос­ходит частоту собственных колебаний а > со$. В этом случае величиной щ в знаменателе выражения можно пренебречь по сравнению с со:

та

Аналогичное выражение амплитуды было получено при описании вы­нужденных колебаний тела, не имеющего положения устойчивого равновесия, т. е. при отсутствии пружины.

Амплитуда вынужденных колебаний обратно пропорциональна квадра­ту частоты со.

При частоте со> щ амплитуда вынужденных колебаний убывает с

ростом частоты. Закон убывания — квадратная гипербола (см. рис. 8.4, кривая /).

Если частота вынуждающей силы приближается к частоте собственных колебаний (со —> со$), то знаменатель выражения стремится к нулю. В этом случае амплитуда колебаний резко возрастает, стремясь к бесконечности при со = а>а.

Резонанс—явление резкого возрастания амплитуды вынужденных ко­лебаний при совпадении частоты внешней силы с частотой собствен- \. ных колебаний системы.

Резонансная кривая — график зависимости амплитуды вынужденных. колебаний системы от частоты изменения внешней силы (рис. 8.4, кривая 2). При резонансе внешняя сила действует синхронно со свободными колеба­ниями системы. На протяжении всего периода свободных колебаний направ­ление внешней силы F совпадает с направлением перемещения Ах колеблю- j щегося тела.

Работа, совершаемая внешней силой, при резонансе положительна, по- j этому полная механическая энергия системы

E = E0 + FAx

постоянно возрастает из-за резонансного поглощения энергии. Быстрое увеличение энергии колеблющегося тела ведет к резкому возрастанию ам­плитуды вынужденных колебаний: А ~ у/Е. Именно с этим приближением -связано стремление к бесконечности амплитуды вынужденных колебаний при резонансе.

Потери энергии на трение приводят к уменьшению полной механиче­ской энергии колебаний и соответственно к уменьшению их амплитуды.

Известно, что для прекращения расплескивания воды в ведре необхо­димо изменить темп ходьбы, при этом изменяется частота внешней силы, вызывающей резонансные колебания воды. Избежать нежелательного резо­нанса можно, изменяя частоту собственных колебаний системы. Пластилин, прикрепленный в центре оконного стекла, предотвращает его дребезжание, возникающее при проезде автомашин мимо окон, так как эффективное уве­личение массы стекла изменяет частоту его собственных колебаний.

Мосты в Анжере в 1750 г. и в Петербурге в 1906 г. были разрушены в результате резонанса. Частоты строевого шага марширующих военных сов­пали с частотой собственных колебаний моста. При землетрясении разруша­ются здания одинаковой высоты, так как их собственная частота колебаний определяется высотой и совпадает с частотой колебаний почвы.

Явление резонанса позволяет с помощью сравнительно малой силы получить значительное увеличение амплитуды колебаний и поэтому используется в вибромашинах, в горнодобывающей промышленности, а также при разработке мерзлого грунта. Используется явление резонанса в радио, телевидении, медицине, исследованиях Вселенной.

2. Экспериментальное задание по теме «Элементы термодина­мики»: построение графика зависимости температуры от времени остывания воды

В вашем распоряжении имеются стакан с горячей водой, большой ста­кан с холодной водой (стакан с горячей водой должен помещаться в стакан с холодной водой), термометр, часы с секундной стрелкой.

Опустите термометр в стакан с горячей водой и через равные проме­жутки времени снимайте показания термометра. Для ускорения процесса можно опустить стакан с горячей водой в стакан с холодной водой, при этом необходимо непрерывно помешивать горячую воду. Постройте график зависимости температуры от времени остывания воды.

3. Текст по разделу «Электродинамика», содержащий описание физических явлений или процессов, наблюдаемых в природе или в повседневной навил. Задание на понимание физических терминов, определение явления, его признаков или объяснение явления при помощи имеющихся знаний

Огни святого Эльма В природе наблюдается интересное явление. Иногда в тропическую ночь на мачтах и реях кораблей появляются кисточки холодного пламени. Эти огни известны очень давно. Их видели Колумб и Магеллан, о них писал даже Юлий

Цезарь, который однажды видел такое свечение на копьях своих солдат во вре­мя ночного похода через горы. Не составляет большого труда самим получить такое свечение. Если хорошо натереть лист оргстекла сухой тканью и после этого к листу поднести полураскрытые ножницы остриями к листу, то в затем­ненной комнате можно увидеть как на остриях ножниц появляются дрожащие пучки нитей, светящиеся лиловатым пламенем. В тишине можно услышать легкое шипение или жужжание. Если вместо ножниц к листу оргстекла поднес­ти спичку, то она не зажжется, хотя огонь будет плясать прямо на головке спички. Возникшее свечение холодное. Такое же свечение часто появлялось на шпиле церкви святого Эльма в одном из городов Франции и считалось доброй приметой. Подобное свечение получило название огней святого Эльма.

Ответьте на вопросы к тексту и выполните задание:

1. Какое физическое явление лежит в основе появления огней святого Эльма?

2. Почему не возникает такого свечения на плоской металлической крыше?

3. Опасно ли находиться вблизи возникших огней святого Эльма на ко­рабле?

4. На каком физическом приборе можно получить огни святого Эльма? Продемонстрируйте.

БИЛЕТ № 9

1. Возникновение атомистической гипотезы строения вещества и ее экспериментальные доказательства. Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа. Аб­солютная температура как мера средней кинетической энергии теплового движения частиц вещества

В основе молекулярно-кинетической теории строения вещества лежат три утверждения: вещество состоит из частиц, эти частицы беспорядочно движутся, частицы взаимодействуют друг с другом.

Определим размеры молекул.

Если наблюдать расплывание капельки масла, например оливкового, по поверхности воды, то масло никогда не займет всю поверхность, если сосуд велик. Нельзя заставить капельку объемом 1 мм3 расплыться так, чтобы она заняла площадь поверхности более 0,6 м2. Можно предположить, что при растекании масла по максимальной площади оно образует слой толщиной всего лишь в одну молекулу. Толщину этого слоя нетрудно определить и тем самым оценить размер молекулы оливкового масла.

Объем V слоя масла равен произведению его площади поверхности S на толщину d слоя, т.е. V = Sd. Следовательно, размер молекулы олив-

. 0,001см3, _ 1Л_7

кового масла равен: д=-----------т-«1,7-10 см.

6000 см2

Размеры молекул, в том числе и оливкового масла, больше размеров. атомов. Диаметр любого атома имеет порядок 10 см. Эти размеры так

малы, что их невозможно себе представить. В таких случаях прибегают к помощи сравнений. Вот одно из них.

Если пальцы сжать в кулак и увеличить его до размеров земного шара, то атом при том же увеличении станет размером с кулак.

При очень малых размерах молекул число их в любом макроскопическом теле огромно. Подсчитаем приблизительное число молекул в капле воды мас­сой 1 г и, следовательно, объемом 1 см3. Диаметр молекулы воды равен ~3• Ю-8см. Считая, что каждая молекула воды при плотной упаковке моле-кул занимает объем (З'Ю см), можно найти число молекул в капле, разделив объем капли (1 см3) на объем, приходящийся на одну молекулу:

N= lc;3 =з,7-ю22.

(3 10-8)3 см3

При каждом вдохе вы захватываете столько молекул, что если бы все они после выдоха равномерно распределились в атмосфере Земли, то каждый житель планеты при вдохе получил бы 2-3 молекулы, побывав­шие в ваших легких.

Массы отдельных молекул и атомов очень малы. Например, в 1 г воды содержится 3,7-1022 молекул. Следовательно, масса одной молекулы во­ды (Н20) равна:

от = —1£_ = 2,7-10"23г. 3,7-1022

Массы такого же порядка имеют молекулы других веществ, исключая огромные молекулы органических веществ, например, белки имеют мас­сы, в сотни тысяч раз большие, чем массы отдельных атомов. Но все равно их массы в макроскопических масштабах (граммах и килограммах) чрезвычайно малы.

Так как массы молекул очень малы, удобно использовать в рас­четах не абсолютные значения масс, а относительные. По международному

соглашению массы всех атомов и молекул сравнивают с — массы атома

углерода (так называемая углеродная шкала атомных масс).

Относительной молекулярной (или атомной) массой вещества М называ­ют отношение массы молекулы (или атома) т0 данного вещества к — массы атома углерода тй

Мш-JSL-.

Относительные атомные массы всех химических элементов точно измерены. Складывая относительные атомные массы элементов, входящие в со­став молекулы вещества, можно вьиислить относительную молекулярную массу вещества. Например, относительная молекулярная масса углегл-

4)

слого газа С02 приближенно равна 44, так как относительная атомная масса углерода равна 12, а кислорода 16: 12 + 2-16'=44.

Количество вещества наиболее естественно было бы измерять числом молекул или атомов в теле. Но число молекул в любом макроскопиче­ском теле так велико, что в расчетах используют не абсолютное число молекул, а относительное.

В Международной системе единиц количество вещества выражают в молях. Один моль — это количество вещества, в котором содержится: столько же молекул или атомов, сколько атомов содержится в углероде I массой 0,012 кг. Значит, в 1 моль любого вещества содержится одно и то же число атомов или молекул. Это число атомов обозначают Л^ и называют: постоянной Авогадро (в честь итальянского ученого XIX в.). Для определе­ния постоянной Авогадро надо найти массу одного атома углерода. Грубая оценка: массы может быть произведена так, как это было сделано выше для массы молекулы воды (наиболее точные методы основаны на отклонении пучков ионов электромагнитным полем).

Постоянную Авогадро можно определить, если разделить массу угле- j рода, взятого в количестве одного моля, на массу атома углерода:

N<= °'012, =6,02.1023моль-'. 1,995-10"26

Наименование моль"1 указывает, что NA — число атомов в одном моле j любого вещества. Если количество вещества v = 2,5 моль, то число моле­кул в теле

N - \NA, Отсюда видно, что количество вещества V равно отношению числа, молекул N в данном теле к постоянной Авогадро, т.е. к числу молекул в 1 моль вещества:

_ Л

Огромное значение постоянной Авогадро показывает, насколько малы микроскопические масштабы по сравнению с макроскопическими Тело, обладающее количеством вещества 1 моль, имеет привычные для нас мак­роскопические размеры и массу порядка нескольких десятков граммов.

Наряду с относительной молекулярной массой М в физике и химии ши­роко используют понятие молярная масса. Молярной массой М вещества называют массу вещества, взятого в количестве одного моля.

Согласно такому определению молярная масса вещества равна произвс-1 дению массы молекулы на постоянную Авогадро:

U = m0NA.

Масса т любого количества вещества равна произведению массы одной молекулы на число молекул в теле:

т = m^N.

Заменив NЛ и /V в формуле их выражениями, получим

_ т V~M ' Английский ботаник Р. Броун впервые наблюдал это явление в 1827 г., рассматривая в микроскоп взвешенные в воде споры плауна. Позже он рас­сматривал и другие мелкие частицы камня. Сейчас для наблюдения бро­уновского движения используют частички краски гуммигут, которая нерас­творима в воде. Эти частички совершают беспорядочное движение. Самым поразительным и непривычным для нас является то, что это движение ни­когда не прекращается. Мы ведь привыкли к тому, что любое движущееся тело рано или поздно останавливается.

Броуновское движение — тепловое движение, и оно не может прекра­титься. С увеличением температуры интенсивность его растет.

Доказать существование значительных сил притяжения между атомами и молекулами несложно. Если бы между молекулами не существовало сил притяжения, то все тела при любых условиях находились бы только в газообразном состоянии. Но одни сипы притяжения не могут обеспечить су­ществования устойчивых образований из атомов и молекул. На очень малых расстояниях между молекулами обязательно действуют силы от­талкивания. Благодаря этому молекулы не проникают друг в друга и куски вещества никогда не сжимаются до размеров одной молекулы.

Молекула — это сложная система, состоящая из отдельных заряженных частиц: электронов и атомных ядер. Хотя в целом молекулы электрически нейтральны, тем не менее между ними на малых расстояниях действуют значительные электрические силы: происходит взаимодействие электронов и атомных ядер соседних молекул.

Если молекулы находятся на расстояниях, превышающих их размеры в не­сколько раз, то силы взаимодействия практически не сказываются. Силы между электрически нейтральными молекулами являются короткодействующими.

На расстояниях, превышающих 2-3 диаметра молекул, действуют си­лы притяжения. По мере уменьшения расстояния между молекулами сила притяжения сначала увеличивается, а затем начинает убывать и убывает до нуля, когда расстояние между двумя молекулами становится равным сумме радиусов молекул.

При дальнейшем уменьшении расстояния электронные оболочки атомов начинают перекрываться, и между молекулами возникают быстро нарастающие силы отталкивания.

Поиск по сайту: