Качественная задача по теме «Маг-

Шиитное поле» В однородное магнитное поле с индукцией В со скоростью и влетает частица массой т и за­рядом q перпендикулярно линиям магнитной в индукции. Как будет двигаться эта частица в

магнитном поле? 'ТТТТ7ТТТ На движущуюся заряженную частицу в маг-

Рис. 9.1 нитном поле действует сила Лоренца, которая

направлена перпендикулярно скорости движения частицы, следовательно, I частица будет двигаться по окружности (рис. 9.1).

3. Текст по разделу «Механика», содержащий описание исполь- I зования законов механики в технике. Задание на понимание основ- ] ных принципов, лежащих в основе работы описанного устройства

От Галилея до современности

Маятник обладает удивительным свойством — оно казалось удивитель- 1 ным Галилею, измерявшему время по числу биений пульса, оно кажется 1 таким же и современному человеку, пользующемуся секундомером. Заклю-чается оно в том, что колебания маятника и с малой амплитудой и с бс шой амплитудой совершаются практически за одно и то же время. Если I сначала колебания происходят с очень большим отклонением, скажем на I

80° от вертикали, то при затухании колебаний до 60...40...20° периода уменьшится лишь на несколько процентов; а при уменьшении отклонений! от 20° до едва заметного период изменяется меньше чем на 1%. При откло-Я нениях меньше 5° период остается неизменным с точностью до 0,05%.

Это свойство маятника оказалось не только удивительным, но и полез-в ным. Галилей предложил использовать маятник в качестве регулятора в! часах. Лишь столетие спустя после Галилея часы с маятниковым регулято-Я ром вошли в обиход. Однако мореплаватели нуждались в точных часах дляи измерения долготы на море. Была объявлена премия за создание морскихЯ часов, которые позволяли бы измерять время с достаточной точностью.» Премию получил Гариссон за хронометр, в котором для регулирования хода использовалось маховое колесо (баланс) и специальная пружина.

Свойство независимости периода колебаний маятника от амплитуды на-Я зывается изохронностью.

Ответьте на вопросы к тексту:

1. Одинакова ли скорость движения маятника?

2. Постоянно ли ускорение при движении маятника?

3. Отчего зависит период колебаний?

4. В чем заключается свойство изохронности?

БИЛЕТ № 10

1. Давление газа. Уравнение состояния идеального газа (уравнеЯ ние Менделеева — Клапейрона). Изопроцессы

За идеальный газ принимают модель, состоящую из материальных той чек, между которыми отсутствуют силы, действующие на расстоянии, Щ которые сталкиваются между собой как упругие шары. При такой моделИ свойства различных газов не должны существенно отличаться друг от др)Я га. Свойства различных разреженных газов не зависят от специфики сиЛ взаимодействия между отдельными молекулами.

Молекулярно-кинетическая теория выясняет взаимосвязь микро- и мвяШ роскопических параметров.

Свободный газ может неограниченно расширяться, занимая весь пре­доставленный объем, так как силы притяжения между молекулами малы

Давление газа — результат ударов молекул. Найдем давление газа, нахо­дящегося в цилиндрическом сосуде, на поршень площадью S (рис 10 1)

Если поршень расположен перпендикулярно оси X то давление га­за равно отношению силы Fx, действующей на поршень вдоль оси X к

его площади S: р = ——.

О

Сила Fx является результи­рующей силой ударов молекул о поршень: Fx = FXAN, где F[ — сила удара одной мо­лекулы, AN — полное число ударов молекул о пошнень. Чептя

сверху (знак усреднения) означает среднее значение силы F% по скоростям молекул.

Найдем сначала силу удара о поршень одной молекулы. Согласно вто­рому закону Ньютона, На молекулу (атом) со стороны поршня действует сила

At где Ли — изменение скорости молекулы за время удара At.

По третьему закону Ньютона на поршень со стороны молекулы дейст­вует сила /j = -Fa:

в А&

At При упругом ударе молекулы о поршень компонента ее скорости по оси У не изменяется, а компонента по оси X изменяет направление на противопо­ложное. Изменение скорости за промежуток времени At равно:

Av = \0-v0\ = 2vx, где v и va — скорости молекулы до и после удара о поршень, vx — про­екция скорости молекулы на осьЛ: Тогда F = т —*- ■

1 " At Рассчитаем теперь полное число ударов молекул о поршень. За промежу­ток времени At с поршнем сталкиваются только те молекулы, которые ус­певают долететь до него за это время. Они находятся в цилиндре объемом ДI' с основанием 5 и образующей Vx At. Следовательно, полное число ударов мо­лекул о поршень равно числу этих молекул:

AN=-nAV = -nSVxAt, 2 2 х

где п — концентрация частиц (число частиц в единице объема). Множитель

~ введен в формулу в связи с тем, что среди всех молекул, хаотически дви-

•'5

жущихся по оси X, лишь половина их движется в положительном направле­нии оси. Объединив уже известные формулы, находим давление газа на поя шень:

1 nSVrAt2m..vx -2,,ч

Р = Т----С., =«№ d)

2 SAt

Вследствие хаотичности теплового движения молекул их движение мо4 жет происходить равновероятно в любом направлении. Поэтому средние квадраты скорости по осям X Y и Z равны: v2 = й2 = v].

Но v2 = v] + v2 + v]. Усредняя это выражение по скоростям, имеем U2=v2 + v2 + v2 = 3v2,

-2 V2

соответственно vr = —.

х 3

Подставляя полученное равенство в выражение (1), ползаем основна уравнение молекулярно-кипетической теории идеального газа:

1 -2

p = -nmav.

Макроскопическая величина (в данном случае давление) с помощьн модели идеального газа определяется этой формулой через микроскопически параметры: массу молекулы, концентрацию молекул и средний квадрат ско роста их хаотического движения. Умножив и разделив правую часть ра венства на 2, можно получить еще одну форму записи основного уравнени молекулярно-кинетической теории идеального газа:

2 =

Р = -пЕк,

где Ек — средняя кинетическая энергия молекул. В данной формуле кон центрация частиц характеризует число ударов молекул о поршень, а средня кинетическая энергия молекул определяет интенсивность одного удара.

Давление идеального газа равно двум третям средней кинетической энц гии поступательного движения молекул, содержащееся в единице объема.

Если газ представляет собой смесь идеальных газов, молекулы каждог газа ударяют поршень независимо друг от друга В соответствии с принципов суперпозиции, силы давления газов, составляющих смесь (парциальчьЯ давления), суммируются по закону Дальтона.

Давление смеси идеальных газов равно сумме парциальных давлениЛ входящих в нее газов.

Например, атмосферное давление складывается из парциальных давлИ ний азота, кислорода и других газов.

В результате большого числа столкновений между молекулами уста наш ливается стационарное равновесное состояние газа — состояние, при кот^ж ром число молекул в заданном интервале скоростей остается постоянным.

Важнейшим макроскопическим параметром, характеризующим стациИ нарное равновесное состояние любого тела, является его температура.

Температура тела — мера средней кинетической энерггш хаотического поступательного движения его молекул.

Средняя кинетическая энергия хаотического поступательного движе­ния молекул тела пропорциональна термодинамической (или абсолютной) температуре:

2 2 где к = 1 38 ■ 10~23 Дж/К — постоянная Больцмана. Единица термодинамиче­ской температуры — кельвин (К); 1 К = 1 °С. Постоянная Больцмана являет­ся коэффициентом, переводящим температуру из градусной меры (К) в энергетическую (Дж) и обратно.

Кинетическая энергия не может быть отрицательной. Следовательно, не может быть отрицательной и термодинамическая температура. Она обра­щается в нуль, когда средняя кинетическая энергия молекул становится равной нулю, являясь абсолютным нижним пределом термодинамической температуры.

Абсолютный нуль температуры (О К) — температура, при которой Оолжно прекратиться движение молекул. Абсолютный нуль термодина­мической температуры по шкале Кельвина соответствует -273,15 °С Связь между температурными шкалами Цельсия и Кельвина определяется соотношениями:

I °с = Г-273, T = t °C + 273.

В быту чаще всего для измерения температуры используют жидкостный термометр. В качестве наполнителя используют ртуть, спирт, пентан.

Для измерения температуры тела термометр приводят в контакт с ним В процессе теплопередачи между телом и термометром устанавливается тепловое равновесие. За Международную практическую шкалу темпера­тур принята шкала Цельсия. В качестве основных точек приняты темпе­ратура плавления льда и температура кипения воды при нормальном ат­мосферном давлении (10s Па). Существенный недостаток жидкостных термометров — различные изменения объема жидкостей при одинаковом нагревании.

Для описания состояния идеального газа шкала Цельсия оказалась не­удобной из-за произвольных точек температурной шкалы (температура таяния льда и температура кипения воды). Возникшую необходимость в создании новой шкалы решил в 1848 г. У. Томсон (лорд Кельвин).

Рассмотрим три разных по вместимости сосуда, наполненных разны­ми газами: азотом, кислородом и гелием. Поместим сначала эти сосуды в лед при температуре 0 °С и подождем, когда между газами и льдом уста­новится тепловое равновесие. Для каждого газа можно измерить его дав­ание и объем. Концентрацию газа выразим по формуле

N m л/ V MV А 1 масса газа, М — молярная масса, УА — постоянная Авогалро

*7

Выражение pV/N оказалось для всех трех газов одинаково и равно 3.76 ■ Ю-21 Дж. Если сосуды перенести в кипящую воду, то выражение pV/N тоже будет для всех трех газов одинаково и равно 5,14 • Ю-21 Дж.

Величина pV/N зависит только от температуры, т.е. можно считать, что pY'N пропорционально температуре. За единицу абсолютной температуры взяли 1 К, значение которого равно градусу Цельсия:

N где к — коэффициент пропорциональности, который называют постоянной Больцмана. Для вычисления постоянной Больцмана найдем разность отно­шения величин pV/N при 0 и 100 °С:

РтУг РУ\ _ ],(Т Т\

n2 n, (г т;

отсюда

к (5,14-3,76)10-21Дж ■ ш-2зДж

100 К ' К

Зная постоянную Больцмана, можно найти температуру по шкале Цельсия:

*Г,=3,76-10~21Дж, Г, = 3,76'10„ =237,15 К=-0°С. 1,38-10"23

Достичь абсолютного нуля невозможно. В настоящее время удалось

dV достичь темперагуры, равной 0,0001 К. Выражение —— = кТ можно пере­до

писать так

р = пкТ.

Сопоставив эти выражения с основным уравнением МКТ, получим

Ё = -кТ

Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.

Уравнение состояния идеального газа связывает между собой толыа макроскопические параметры: давление р, объем V и температуру Т. Давле­ние идеального газа определяет уравнение

р = пкТ. (2)

где п — концентрация молекул в единице объема

N п\

«= —, (3)

V

m а их количество N=-----NA. (4)

М Л m — масса газа, А/ — молярная масса газа, NA — постоянная Авогадро Подставляя уравнения (2) и (3) в (4), получим выражение

рУтЯ-.шт (5)

м

4Ь

Произведение постоянной Больцмана к и числа Авогадро /VA называют универсальной газовой постоянной и обозначают R:

/г = 1,38-ю-21^-б,02-ю23—— = 8,31 Дж.

К моль моль-К

Подставив универсальную газовую постоянную в уравнение (4), получим

PV = ^-RT М

Это уравнение называют уравнением Менделеева — Клапейрона.

Универсальная газовая постоянная показывает, какую работу надо со­вершить над молем газа, чтобы изменить его внутреннюю энергию на 1 К.

Уравнение состояния идеального газа не выполняется при низких тем­пературах и высоких давлениях, т.е. в том случае, когда нельзя пренебре­гать размерами молекул и силами взаимного притяжения.

Многие процессы изменения состояния газов в природе и в тепловых машинах происходят так, что один из трех макроскопических параметров (объем, давление или температура) остается (или специально поддерживается) постоянным. Два других параметра при этом изменяются.

Изопроцесс — процесс, при котором один из макроскопических пара­метров состояния данной массы газа остается постоянным.

Рассмотрим последовательно возможные изопроцессы.

Изотермический процесс — процесс изменения состояния определенной массы газа при постоянной температуре.

При этих условиях из уравнения Менделеева — Клапейрона

PV- 2- RT.

м

Для газа данной массы при постоянной температуре произведение дав­ления газа на его объем постоянно:

P\V\=P2V2-

Давление газа при изотермическом процессе, как следует из закона Бой-ля — Мариотта, обратно пропорционально его объему:

const '" — ■ График такой обратно пропорциональной зависимости — гипербола, называемая для данного процесса изотермой (рис. 10.2).

Изобарный процесс — процесс изменения состояния определенной массы газа при постоянном давлении.

При этих условиях из уравнения Менделеева — Клапейрона следует закон Гей-Люссака: для газа данной массы при постоянном давлении отношение объема газа к его термодинамической температуре посто­янно:

График такой линейной зависимости — прямая, называемая для дан­ного процесса изобарой (рис. 10.3). При изобарном расширении темпе­ратура газа и соответственно средняя квадратичная скорость молекул возрас­тают за счет количества теплоты Q подводимого к газу.

Изохорный процесс — процесс изменения состояния определенной массы газа при постоянном объеме.

При этих условиях из уравнения Менделеева — Клапейрона следует закон Шарля: для гам данной массы отношение давления газа к его термодина- I ми ческой температуре постоянно:

Г, Т2

График такой зависимости — прямая, называемая для данного процесса изохорой (рис. 10.4).

2. Экспериментальное задание по теме «Динамика»: проверка зависимости периода колебания маятника от длины нити (или не­зависимости периода от массы груза)

В вашем распоряжении имеется штатив с закрепленной лапкой, к кото­рой привязана нить длиной 1 м (на конце нити закреплен металлический шарик), секундомер, сантиметровая лента. Период колебаний математиче-

ского маятника определяется по формуле Т = 2тг /—.

IS

1. Установите штатив на краю стола. Шарик должен висеть на расстоя- I нии 3-5 см от поверхности стола.

2. Отклоните маятник от положения равновесия на 5-8 см и отпустите его.

3. Измерьте длину подвеса сантиметровой лентой (можно другим измс-рительным прибором).

4. Рассчитайте период собственных колебаний маятника, например, при длине нити 1 м. Возьмите значение g на вашей широте.

5. Измените длину маятника, например 0,25 м.

6. Снова рассчитайте период колебаний маятника.

7. Сравните результаты.

8. Сделайте вывод о том, как зависит период свободных колебаний ма- j ятника от его длины.

3. Текст по разделу «Электродинамика», содержащий описание использования законов электродинамики в технике. Задание на понимание основных принципов, лежащих в основе работы опи­санного устройства

Действие магнитного поля на проводник с током

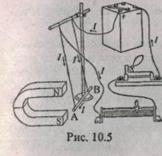
Воспользуемся магнитным полем дугооб­разного магнита, а электрическую цепь собе­рем согласно рис. 10.5.

Проводник АВ представляет собою пря­молинейный участок цепи, находящийся в магнитном поле дугообразного магнита. При пропускании электрического тока на­блюдается отклонение проводника с током в магнитном поле. Меняя направление тока, можно наблюдать изменение направления отклонения проводника с током в магнит­ном поле.

В 1820 г. французский физик Ампер экспериментально установил, от каких физических величин зависит эта сила.

Сила, с которой магнитное поле действует на помешенный в него отрезок проводника с током, равна произведению силы тока, модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между направлениями тока и магнитной индукции:

F = IB At sm а.

Существует правило, по которому опреде­ляется направление силы Ампера. Если в маг­нитном поле будет находиться рамка с током, то на нее действует пара сил, которая создает вращающий момент для рамки (рис. 10.6): М = ISB sin a.

Поворот рамки с током в магнитном поле используют в электроизмерительных приборах магнитоэлектрической системы, например в амперметрах. В магнитном поле между посто­янным магнитом и цилиндром из мягкого желе-

за располагается катушка, способная вращаться вокруг горизонтальной оси. При такой конструкции вращающий момент, действующий на катушку, максимален. Вращающий момент пропорционален силе измеряемого тока и числу витков в катушке. Измеряемая сила тока прямо пропорциональна углу отклонения стрелки.

Ответьте на вопросы к тексту:

1. Почему магнитное поле действует на проводник с током, находящий­ся в этом магнитном поле?

2. Сформулируйте правило для определения направления силы Ампера.

3. В каких единицах измеряют магнитную индукцию?

4. Возможно ли использовать поворот рамки- с током в магнитном поле в приборах для измерения напряжения в электрической цепи? Как называ­ют такие приборы?

БИЛЕТ №11

1. Испарение и конденсация. Насыщенные и ненасыщенные па­ры. Влажность воздуха

Процесс перехода молекул из жидкости в пар называют испарением. Молекула пара испаряется с поверхности жидкости в воздух, если ее кине­тическая энергия больше потенциальной энергии притяжения к другим молекулам. Испарение происходит при любой температуре жидкости. Средняя кинетическая энергия молекул определяется как Е=3/2кТ. Если энергия молекул больше этого значения, они покинут жидкость, т.е. испа­рятся. Количество теплоты, необходимое для испарения (парообразования) 1 кг жидкости при постоянной температуре называют удельной теплотой испарения (г):

Q = rm.

При парообразовании подводимое количество теплоты расходуется на разрыв связей между молекулами жидкости. Испаряющиеся из жидкости молекулы образуют над ней пар. В результате их хаотического движения часть молекул возвращается на поверхность жидкости за счет сил притяже­ния (процесс конденсации), увеличивая энергию жидкости. Количество теп­лоты, получаемое жидкостью при конденсации, равно количеству теплоты, теряемому при ее испарении Если наблюдать процесс испарения жидкости в закрытом сосуде, то концентрация пара может достигнуть такого значения, когда число молекул пара, конденсирующихся за определенный промежуток времени, равно числу молекул жидкости, испаряющихся с ее поверхности за это же время. Так как р - пкТ, то при данной температуре давление пара большим быть не может, и пар в таком состоянии называют насыщенным.

При одной и той же температуре содержание в воздухе водяного пара может изменяться от нуля до состояния насыщения. С ростом температуры жидкости увеличивается число испаряющихся молекул и соответственно конденсирующихся молекул пара, поэтому давление насыщенного пара возрастает при увеличении температуры жидкости.

Давление насыщенного пара зависит от молекулярной структуры жид­кости. Давление насыщенного пара жидкости, состоящей из сильно взаимо­действующих друг с другом молекул, меньше, чем давление насыщенного пара жидкости, состоящей из слабо взаимодействующих молекул. В окру­жающей нас атмосфере пар редко бывает насыщенным из-за нарушения равновесия процессов испарения и конденсации. Этому способствует пере­мещение слоев воздуха в атмосфере. При одной и той же температуре со­держание в воздухе водяного пара может изменяться от абсолютно сухого i воздуха до состояния насыщения. Степень влажности характеризуется от- ' носительной влажностью.

Относительная влажность воздуха — процентное отношение концен­трации водяного пара в воздухе к концентрации насыщенного пара при той же температуре:

Ф = — 100%. "™ Так как концентрация пара связана с давлением, то относительную влажность можно выразить как процентное отношение давления пара в воздухе и давления насыщенного пара при той же температуре:

<р = -£и-.Ю0%.

Рнп

Существуют три способа определения влажности воздуха: метод точки росы, волосной гигрометр и (наиболее точный из них) психрометр Августа. От влажности зависит интенсивность испарения влаги с поверхности кожи человека. Испарение влаги имеет большое значение для поддержания тем­пературы тела постоянной. Наиболее благоприятная для человека относи­тельная влажность воздуха 40-60 %. Знание влажности помогает метеоро­логам правильно предсказывать погоду. На производствах, где возникает статическое электричество, например изготовление радиодеталей из тек­столита, существует служба, отвечающая за влажность воздуха в цехах. В пищевой промышленности для поддержания нормального технологическо­го процесса необходима определенная влажность. Влажности порядка 70 % требует и хранение книг, произведений искусства. В музеях и хранилищах книг на стенах висят психрометры — приборы для определения влажности.

2. Экспериментальное задание по теме «Электромагнитная ин­дукция»: наблюдение явления электромагнитной индукции

В вашем распоряжении имеется оборудование для исследования явления электромагнитной индукции: дугообразный магнит, 2 проволочные катушки с сердечниками, миллиамперметр, соединительные провода, ключ, магнитная стрелка (компас), реостат.

Соберем электрическую цепь (рис. 11.1).

1. Приставьте сердечник к одному из полюсов дугообразного магнита и вдвиньте внутрь катушки, наблюдая одновременно за стрелкой миллиам­перметра.

2. Повторите наблюдение за стрелкой, но при этом выдвигайте сердеч­ник из катушки.

3. Повторите опыт, меняя полюса магнита.

4. Примените для всех четырех случаев правило Ленца.

5. Вставьте в обе катушки сердечники, расположите их так, чтобы оси совпадали, и присоедините вторую катушку через

> выключатель к источнику питания.

6. Наблюдайте отклонение стрелки при замыкании и размыкании цепи.

7. Сделайте вывод.

3. Текст по разделу «Квантовая физика и элементы астрофи­зики», содержащий описание использования законов квантовой, атомной или ядерной физики в технике. Задание на понимание основных принципов, лежащих в основе работы описанного уст­ройства

Пока еще недоступная энергия

При слиянии легких ядер выделяется энергия. Как научиться управ­лять этой энергией? Задача состоит в том, чтобы, преодолев электриче­ское отталкивание, сблизить легкие ядра на достаточно близкие рас­стояния друг от друга, где уже начинают действовать между ними ядер­ные силы притяжения. Если бы можно было заставить два протона и два нейтрона объединиться в ядро атома гелия — или же четыре протона с соответствующими превращениями, -— то при этом выделилась бы ог­ромная энергия. Заставить сблизиться ядра можно с помощью нагрева до высоких температур, когда в результате обычных столкновений ядра смогут сблизиться на столь малые расстояния, чтобы ядерные силы вступили в реакцию, и произошел синтез. Начавшись, процесс синтеза, по-видимому, сможет дать такое количество теплоты, которое нужно для поддержания высокой температуры, необходимой для дальнейших i слияний ядер. Этот многостадийный процесс «горения» водорода, в результате которого происходит синтез ядер гелия, является источником непрерывного потока солнечной радиации. Проблема использования синтеза ядер в мирных целях, например для производства электриче­ской энергии, упирается в очень трудную проблему удержания реак­ции. Газ должен быть раскален до температуры порядка 50 000 000 °С, и любая твердая оболочка, соприкоснувшись с ним, обратится в пар. Если к тому же при синтезе выделяется полезное тепло, то задача удержания реакции еще более усложняется.

В настоящее время ведутся исследования по удержанию реагирую­щих веществ с помощью электромагнитного поля. Можно подвешивать в воздухе магнит с помощью других магнитов, хотя такое равновесное положение и является неустойчивым. Если пропускать ток достаточно большой силы через газ, то образуются потоки электронов и положи­тельных ионов, движущихся навстречу друг другу. Под действием маг-. нитного поля, которое окружает ток, такой поток движущихся зарядов будет сжиматься в узкий шнур. В этом заключается так называемый пинч-эффект. Пинч-эффект и силы, создаваемые магнитными полями, меняющимися по определенному закону, можно использовать для удер-; жания плазмы — смеси быстро движущихся ядер и электронов в «маг-: нитной бутылке», где происходит реакция синтеза.

Ответьте на вопросы к тексту:

1. Что означает слово синтез? 1

2. Всегда ли при ядерной реакции выделяется энергш.. j

3. Что такое плазма? j

4. Каковы проблемы управления термоядерным синтезом? |

БИЛЕТ № 12

1. Работа в термодинамике. Внутренняя энергия. Первый за кон термодинамики. Адиабатный процесс. Второй закон термоди намики

Внутренняя энергия тела — одна из основных величин, используемых термодинамике.

Внутренняя энергия тела — сумма кинетической энергии хаотически.•о (теплового) движения частиц (атомов или молекул) тела и потенци спьной энергии их взаимодействия.

Для идеального газа потенциальная энергия взаимодействия частиц пре псбрежимо мала по сравнению с их кинетической энергией теплового движе пия. Поэтому внутренняя энергия идеального газа определяется кинетиче ской энергией движения частиц.

Средняя кинетическая энергия одного атома

к 2 распределяется по степеням свободы, по осям X, Y, Z одинаково. Внутрен няя энергия U одноатомного газа, состоящего из N атомов, в N раз болыш шергии одного атома:

U = NEk=-NkT. 2

Разделив и умножив это выражение на молярную массу

M=mNM

получим

3NmNAKT__3(NmWAk)T ИШ v =ljHRT 2 М 2 М 2М '

Внутренняя энергия данной массы идеального газа зависит лишь от одно-■ -о макроскопического параметра — термодинамической температуры.

Используя уравнение Менделеева — Клапейрона, можно представить выражение для внутренней энергии идеального одноатомного газа в виде:

U = -pV

I aj называют двухатомным, если каждая его молекула состоит из двух атомов. Каждый атом может двигаться по трем направлениям, поэтому пол­ное число возможных направлений движения такой молекулы равно 6. Связь, существующая между атомами в двухатомной молекуле, уменьшав! число степеней свободы на единицу. Поэтому число степеней свободы для двухатомной молекулы равно пяти. Средняя кинетическая энергия двух­атомной молекулы Ек =—кТ. Соответственно внутренняя энергия идеального двухатомного газа равна:

иЛЛ-ктЛрг.

Формулы для внутренней энергии идеального газа можно обобщить: 1

УшНО-кгЛру, •

2 А/ 2

где i — число степеней свободы молекул газа.

Известно, что изменение температуры тела приводит к изменению его ■■ внутренней энергии. Изменение внутренней энергии AU равно разности ее конечного и начального значений

Аи. = и2-иг.;

Существует два способа изменения внутренней энергии системы: теп- " лообмен и совершение работы.

Теплообмен — процесс передачи энергии от одного тела к другому без со- \ вершения работы. Мерой такой передачи энергии является количество теплоты. 1

Количество теплоты, получаемое телом, — это энергия, передаваемая; телу извне в результате теплообмена. При нагревании тела увеличивается! его температура и внутренняя энергия. Для уменьшения внутренней энер- ', гии тела можно привести его в контакт с более холодным телом. В результате 1 теплообмена температура и внутренняя энергия горячего тела уменьшаются, но работа не совершается, так как тела не перемещаются.

За счет изменения внутренней энергии тела работа при теплообмене не совершается

За счет совершения работы может происходить увеличение температуры и внутренней энергии системы, например, при вращении лопастей в жидко­сти и сжатии газа в сосуде. Для перехода внутренней энергии тела в меха­ническую работу необходимо хаотическое движение его молекул преобразо­вать в упорядоченное движение другого тела. В качестве такого тела наибо­лее целесообразно использовать поршень в цилиндре, перемещающийся под давлением газа, заполняющего цилиндр. Сила давления газа совершает работу при его расширении за счет изменения внутренней энергии газа.

Вычислим работу, совершаемую силой давления F газа при его расшире­нии от начального объема Vt до конечного V2 (рис. 12.1).

Будем считать, что поршень, площадь поперечного сечения которого S, перемещается на высоту А, а сила давления газа в процессе перемещения оста­ется постоянной. Работа силы давления газа при таком перемещении равна:

A = FhcosO = — Sh.

Так как среднее давле-

_ F ние газа р = —, изменение S

его объема

AV = V2-Vl=Sh, то выражение для работы газа можно представить в виде:

А = pAV.

Работа, совершаемая газом, равна произведению среднего давления /if ш на изменение его объема:

A = Wi~Vx).

При расширении (AV > 0) газ совершает положительную работу, от-1>,шая энергию окружающим телам.

При сжатии (AV < О) работа, совершаемая газом, отрицательна. Внут-/пшяя энергия газа при сжатии увеличивается.

При изохорном процессе (V- 0) работа газом не совершается: А =0.

Рассмотрим изобарное расширение газа, имеющего давление р, от началь­ник) объема Vj до конечного V2. Работа, совершаемая газом, равна площади прямоугольника под изобарой со сторонами;? и (V2 - Vi) (рис. 12.2).

При изотермическом расширении газа его давление изменяется по ги-ik-рболическому закону. Выделим на изотерме небольшой участок, соответ-t шующий малому изменению объема AV (рис. 12.3). Проведем перпенди-i. ляры из концов участка до пересечения с изотермой и обозначим через / среднее давление газа при таком изменении объема. Работу, совершае­мую газом при расширении, определяет площадь заштрихованной трапеции. 111 площадей подобных трапеций складывается полная площадь под изотер­мой, численно равная работе при изотермическом расширении газа:

м к,

Работа, совершаемая газом в процессе его расширения (или сжатия) при чобом термодинамическом процессе, численно равна площади под кривой, и юбражающей изменение состояния газа наpV-диаграмме (рис. 12.3).

В общем случае внутренняя энергия может изменяться одновремен­но как за счет теплообмена с окружающими телами, так и за счет со-нсршения работы внешними силами.

Первый закон термодинамики (закон сохранения энергии для те­пловых процессов): изменение внутренней энергии системы при ее переходе из одного состояния в другое равно сумме количества теп­лоты, подведенного к системе извне, и работы внешних сил, дейст­вующих на нее:

AU = Q + AeH.

Для изолированной системы, которая не обменивается теплотой с ок­ружающими телами (Q = 0) и над которой не совершается работа внешних сил (Авн = 0), внутренняя энергия равна

Д£/ = £/2-1/, =0, или U2 = UU i

i т.е. внутренняя энергия замкнутой, изолированной системы сохраняется. 1

В термодинамике наибольший интерес представляет преобразование]

внутренней энергии в работу, совершаемую газом. Эта работа отличаете

ся от раооты внешних сил только знаком: ]

4s» = —/* • I

Действительно, пусть при сжатии газа внешней силой Fm поршень смещается в направлении силы на h. Тогда

Am=FaihcosQ = Fmh. I

По третьему закону Ньютона сила давления газа на поршень равна

F = -Fm, Следовательно, работа, совершаемая силой давления газа, \

А = Fh cos 180° = -F„Hh. j

Первый закон термодинамики можно сформулировать так: количеЯ

ство теплоты, подведенное к системе, идет на изменение ее\

внутренней энергии и на совершение системой работы над внеш-\

ними телами: \

Q = AU + A. \

При изохорном процессе объем газа остается постоянным (AV = 0), поэтому газ не совершает работу (А = 0). Изменение внутренней энергищ газа происходит благодаря теплообмену с окружающими телами:

Q = AU. Если начальная температура газа 7J, а конечная Г2, то

1 ' 2 л/ 1 1М ' гм

т.е. Q = -—RAT.

2М

Нагревание газа (ДГ £ 0) происходит при подведении к нему количест­ва теплоты (Q > 0). При изохорном нагревании давление газа возрастает из-за увеличения средней кинетической энергии молекул. Если от газа отво­дится количество теплоты (Q< 0), то газ охлаждается (AT < 0) и его дав­ление падает.

При изотермическом процессе температура постоянна (ДГ = 0), поэто­му внутренняя энергия не изменяется (Д U = 0). При изотермическом про­цессе количество теплоты, переданное газу от нагревателя, полностью рас* ходуется на совершение работы Q = А. При изотермическом расширении газа, находящегося в цилиндре под поршнем, молекулы газа, сталкиваясь < поршнем, уменьшают свою скорость и соответственно среднюю энергию

II». ному для поддержания постоянной температуры газа к нему подводится щцолнительное количество теплоты. 11ри изотермическом сжатии газа (А < 0) для сохранения постоянной ■ > мпературы от газа отводится определенное количество теплоты (Q < 0). При изобарном расширении газа подведенное к нему количество теп-■ты расходуется на увеличение его внутренней энергии (A U > 0) и на со-сгршениеработы газом (А > 0): Q = AU + A. Ятя изобарного расширения газа от объема Vt до объема ^ при котором ml;ичивается его температура, необходимо большее количество теплоты, ■км при изотермическом процессе, где температура газа не изменяется.

Для наиболее эффективного преобразования внутренней энергии газа в. ьсршаемую им работу следует предотвратить возможные потери внутрен-|' Г: энергии в результате теплопередачи окружающим телам. Поэтому сис-'..чу теплоизолируют.

Теплоизолированная система — система, не обменивающаяся энергией с • ужающими телами (Q = 0). Даже если газ недостаточно теплоизолиро-нщ, то при его быстром расширении или сжатии теплообмен между газом и ■ * -г. ружающими телами за малый промежуток времени не успевает произойти.

Адиабатный процесс — термодинамический процесс в теплоизолиро-■ гшой системе.

Первый закон термодинамики для адиабатного процесса имеет вид:

Д{У + Л = 0, или A = -AU. При адиабатном расширении газа работа увеличивается (А > 0), следо-

ii.i..;.-!iHO,

AU = -—RAT<0. 2М

Это означает, что температура газа уменьшается (АТ< 0) по

I равнению с первоначальной. Понижение температуры газа при адиабат­ном расширении приводит к тому, что его давление уменьшается более I l j:co, чем при изотермическом процессе. На рис. 12.4 приведена адиабата 1-2, проходящая между двумя изотеп-

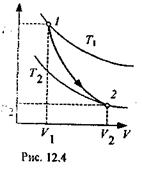
адиаоата 1-J, проходящая между двумя изотер­мами. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатном расширении от объема Pj до объема V2. Адиа­батное сжатие приводит к повышению темпе­ратуры газа, так как в результате упругих со­ударений молекул газа с поршнем их средняя кинетическая энергия возрастает. Например, при быстром сжатии воздуха в цилиндре ку­сочек ваты, смоченный эфиром, воспламеня­ется.

Резкое нагревание воздуха при адиабатном сжатии используют в дизельных двигателях.

Поиск по сайту: