 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Градиентный метод в сочетании с методом наискорейшего спуска
1. Задаем начальные приближения 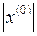 .
.
2. Находим значение целевой функции 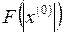 и антиградиента
и антиградиента  в точке
в точке 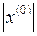 .
.
3. Делам пробные шаги и находим 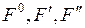 .
.
4. Определяем оптимальную длину шага 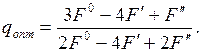
5. Определяем новые приближения оптимизируемых параметров 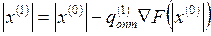 .
.
6. Проверяем выполнение критерия оптимальности 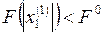 .
.
Вторая итерация выполняется аналогично. Далее проверяем критерий окончания расчетов: 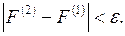 При выполнении условия расчеты заканчиваются, при невыполнении продолжаем итерации.
При выполнении условия расчеты заканчиваются, при невыполнении продолжаем итерации.
20.1 Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента
 В градиентных методах движение всегда осуществляется в направлении наибольшего убывания целевой функции
В градиентных методах движение всегда осуществляется в направлении наибольшего убывания целевой функции 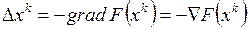 . Вектор градиента определяется через производные функции F(x) по всем независимым переменным
. Вектор градиента определяется через производные функции F(x) по всем независимым переменным 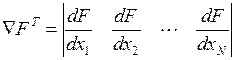 .
.
Таким образом, чтобы воспользоваться рекуррентным выражением градиентного метода  , необходимо на каждом шаге итерационного процесса вычислять значения производных
, необходимо на каждом шаге итерационного процесса вычислять значения производных  . Для организации скорейшего спуска необходимо определение оптимальной длины шага
. Для организации скорейшего спуска необходимо определение оптимальной длины шага  , которая в этом случае удовлетворяет условию
, которая в этом случае удовлетворяет условию  . Это условие означает, что результирующий вектор спуска
. Это условие означает, что результирующий вектор спуска 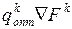 должен быть таким, чтобы новый градиент стал ортогонален предыдущему.
должен быть таким, чтобы новый градиент стал ортогонален предыдущему.
Достоинство этого метода состоит в том что, несмотря на сложность и большой объем вычислений на каждом шаге, он в сочетании с методом наискорейшего спуска дает очень быструю сходимость.
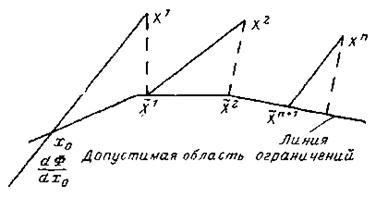
Метод проектирования градиента. Пусть требуется найти минимум выпуклой функции при условии, что независимые переменные удовлетворяют системе из P линейных ограничений в форме неравенств, т. е. 
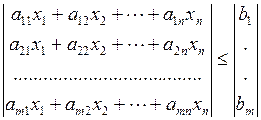 .
.
В начальной точке Х°, фазовые координаты которой удовлетворяют условиям ограничений  , определяется вектор-градиент и в направлении антиградиента производится движение за границу допустимой области до точки x':
, определяется вектор-градиент и в направлении антиградиента производится движение за границу допустимой области до точки x': 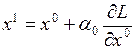 , где
, где  –множитель, определяющий величину шага за границу допустимой области.
–множитель, определяющий величину шага за границу допустимой области.
20.2 Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента
Полученная точка X1 проектируется на поверхность ограничений  , в результате чего определится точка
, в результате чего определится точка  . Затем из точки
. Затем из точки  так же как и из точки Х°, в направлении антиградиента совершается движение за границу допустимой области в точку
так же как и из точки Х°, в направлении антиградиента совершается движение за границу допустимой области в точку 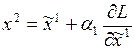 .
.
Полученная точка X2 проектируется на поверхность ограничений, в результате чего получается точка 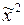 и т. д.
и т. д.
Если начальная точка Х° находится вне допустимой области, она вначале должна быть спроектирована на поверхность ограничений, после чего осуществляется описанная процедура движения. Это позволяет решать задачу от любого начального приближения.
21.1 Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент
При решении задачи оптимизации режима должны учитываться уравнения связи, дающие зависимости между переменными y и x. Количество зависимых переменных M определяется числом уравнений связи, которые можно рассматривать как ограничения, выраженные в форме равенств. В качестве таких ограничений обычно принимаются УУН, записанные в форме баланса токов каждого узла, кроме балансирующего или в форме баланса мощностей каждого узла  (1), где
(1), где  – общее число узлов в системе без балансирующего. Целевую функцию можно представить в виде
– общее число узлов в системе без балансирующего. Целевую функцию можно представить в виде  , где x, y – векторы независимых и зависимых переменных, связь между которыми выражается системой уравнений в виде вектор – функции
, где x, y – векторы независимых и зависимых переменных, связь между которыми выражается системой уравнений в виде вектор – функции 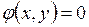 .
.
В градиентном методе необходимо определить направление 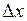 максимального уменьшения целевой функции, не нарушая связей между переменными. Поэтому найдем связь между приращениями зависимых
максимального уменьшения целевой функции, не нарушая связей между переменными. Поэтому найдем связь между приращениями зависимых  и независимых
и независимых 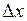 переменных.
переменных.
Рассмотрим точку (х°, у°) с координатами 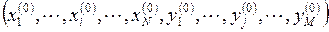 , удовлетворяющую системе равенств
, удовлетворяющую системе равенств 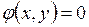 :
:  (2),
(2), 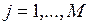 .
.
Это означает, что рассматриваются режимы энергосистемы, удовлетворяющие (1).
Разложив нелинейные уравнения 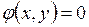 в точке (х°, y°) в ряд Тейлора и ограничившись членами, содержащими производные не выше первого порядка, получим
в точке (х°, y°) в ряд Тейлора и ограничившись членами, содержащими производные не выше первого порядка, получим 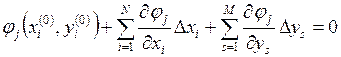 ,
, 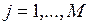 .
.
С учетом (2) в матричной записи последняя система уравнений приобретает вид 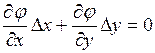 , откуда, переходя к бесконечно малым приращениям, получим
, откуда, переходя к бесконечно малым приращениям, получим  (3).
(3).
Здесь  – матрицы частных производных уравнений связи по независимым и зависимым переменным.
– матрицы частных производных уравнений связи по независимым и зависимым переменным.
С учетом зависимости y(x) целевую функцию F(x,y) можно представить как F(x, y(x)). Выражение градиента приобретает вид
21.2 Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент

что в матричной форме записывается двумя способами:
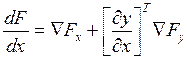 ;
;  (4),
(4), 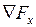 ,
, 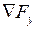 – векторы - столбцы частных производных целевой функции по независимым и зависимым переменным.
– векторы - столбцы частных производных целевой функции по независимым и зависимым переменным.
Вектор производных целевой функции по независимым переменным dF/dx называется приведенным градиентом. С учетом соотношения (3) представим (4) в виде  .
.
Вектор dF/dx рассматривается как возможное направление и используется в рекуррентном выражении итерационной процедуры  .
.
Наряду с методом приведенного градиента ограничения в форме равенств учитывает также метод Лагранжа. При отыскании экстремума целевой функции с учетом ограничений в форме равенств методом Лагранжа вводится новая функция Лагранжа L, в которой все переменные рассматриваются как независимые. В данном случае нет необходимости вычислять матрицу частных производных [dу/dx], в чем и заключается преимущество метода по сравнению с предыдущим. Недостатком метода является увеличение размерности задачи за счет введения неопределенных множителей Лагранжа, число которых равно числу уравнений связи.
22.1 Учет ограничений в форме неравенств при решении задач опт-ии в электроэнергетике. Метод штрафных функций
При оптимизации режима электрической системы задается совокупность ограничений в форме неравенств 

 , определяющая некоторую допустимую область D. В задаче нелинейного программирования необходимо отыскивать относительный экстремум в области D, допуская, что активным может оказаться любое ограничение. В некоторых случаях активные ограничения могут быть выявлены в ходе итерационного процесса решения задачи оптимизации.
, определяющая некоторую допустимую область D. В задаче нелинейного программирования необходимо отыскивать относительный экстремум в области D, допуская, что активным может оказаться любое ограничение. В некоторых случаях активные ограничения могут быть выявлены в ходе итерационного процесса решения задачи оптимизации.
 Пусть
Пусть 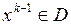 . В результате шага по рекуррентному выражению метода возможных направлений получается точка xk. Если эта точка также принадлежит области D, то осуществляется переход к точке xk+1. Если же
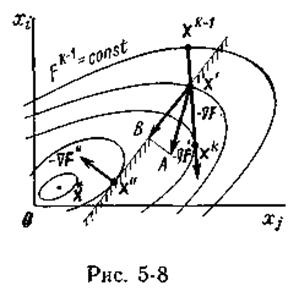
. В результате шага по рекуррентному выражению метода возможных направлений получается точка xk. Если эта точка также принадлежит области D, то осуществляется переход к точке xk+1. Если же 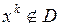 , то необходимо найти граничную точку xk на поверхности области D. В результате выявляется активное ограничение (рис. 5-8), которое можно рассматривать как равенство. Однако правомерность такого перехода должна быть обоснована, так как не исключаются ситуации, подобные представленной на рис. 5-8. Здесь точка
, то необходимо найти граничную точку xk на поверхности области D. В результате выявляется активное ограничение (рис. 5-8), которое можно рассматривать как равенство. Однако правомерность такого перехода должна быть обоснована, так как не исключаются ситуации, подобные представленной на рис. 5-8. Здесь точка 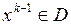 . Движение по антиградиенту
. Движение по антиградиенту 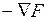 с оптимальной длиной шага приводит в точку
с оптимальной длиной шага приводит в точку 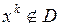 . Пусть найдена граничная точка x'. Если в дальнейшем ограничение рассматривать как равенство, то будет найден экстремум на ограничивающей поверхности в точке x". Как видим, в данном случае решение оказывается неправильным, так как фактически следует найти точку абсолютного минимума
. Пусть найдена граничная точка x'. Если в дальнейшем ограничение рассматривать как равенство, то будет найден экстремум на ограничивающей поверхности в точке x". Как видим, в данном случае решение оказывается неправильным, так как фактически следует найти точку абсолютного минимума  .
.
Метод штрафных функций. Для решения задачи отыскания экстремума целевой функции F (x,y) в допустимых областях Dy и Dz рассматривается новая функция  , которая в отличие от F(x,у) определена в пространстве зависимых переменных при
, которая в отличие от F(x,у) определена в пространстве зависимых переменных при  и
и  (где
(где  рассматриваются в виде переменных, зависимых от x и у). Это свойство новой функции и достигается за счет введения штрафных функций Ш(y) и Ш(z), подчиняющихся условиям:
рассматриваются в виде переменных, зависимых от x и у). Это свойство новой функции и достигается за счет введения штрафных функций Ш(y) и Ш(z), подчиняющихся условиям:
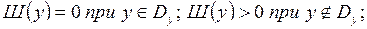
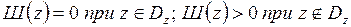 .
.
22.2 Учет ограничений в форме неравенств при решении задач опт-ии в электроэнергетике. Метод штрафных функций
Эти условия означают следующее: если взята некоторая точка хk так, что соответствующие ей зависимые переменные yk и zk удовлетворяют ограничениям 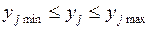 и
и 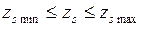 , то штраф равен нулю, в противном случае накладывается штраф в виде некоторой положительной добавки к исходной функции F(x,у). Чем существенней отклонение от допустимой области, тем больше величина штрафа. А так как методы возможных направлений в этом случае основываются на построении такой траектории х°, х1,..., хk, в которой Wk<Wk-1, то при надлежащем выборе функции штрафа движение всегда будет происходить в сторону допустимой области.
, то штраф равен нулю, в противном случае накладывается штраф в виде некоторой положительной добавки к исходной функции F(x,у). Чем существенней отклонение от допустимой области, тем больше величина штрафа. А так как методы возможных направлений в этом случае основываются на построении такой траектории х°, х1,..., хk, в которой Wk<Wk-1, то при надлежащем выборе функции штрафа движение всегда будет происходить в сторону допустимой области.
Штрафные функции должны удовлетворять двум условиям: 1) при их использовании не должны появляться новые локальные минимумы и абсолютный минимум функции W должен совпадать с относительным минимумом исходной целевой функции или быть достаточно близким ему; 2) функция штрафа должна возрастать при увеличении степени нарушения ограничения.
Способ задания квадратичной штрафной функции вида 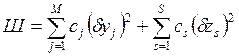 , где
, где 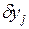 ,
,  – величины, характеризующие степень нарушения соответствующих ограничений. Коэффициенты штрафа
– величины, характеризующие степень нарушения соответствующих ограничений. Коэффициенты штрафа  и
и 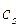 имеют смысл коэффициентов приведения штрафа к размерности целевой функции.
имеют смысл коэффициентов приведения штрафа к размерности целевой функции.
Выбор коэффициента штрафа существенно влияет на сходимость итерационного процесса и точность отыскания минимума целевой функции. Чем больше величина  , тем круче растет функция W вне области D и тем заметнее функция W приобретает свойства «овражности». Чаще всего при овражных функциях удовлетворительная сходимость не обеспечивается. Коэффициент штрафа влияет и на траекторию спуска.
, тем круче растет функция W вне области D и тем заметнее функция W приобретает свойства «овражности». Чаще всего при овражных функциях удовлетворительная сходимость не обеспечивается. Коэффициент штрафа влияет и на траекторию спуска.
23.1 Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе
Преимущество метода Ньютона заключается в том, что количество итерационных шагов невелико. Как и во всяком итерационном методе, расчет начинается с задания некоторой исходной точки 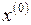 , для которой можно вычислить значение функции
, для которой можно вычислить значение функции 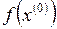 . Аппроксимируем в точке
. Аппроксимируем в точке 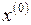 зависимость f(x) некоторой другой функцией
зависимость f(x) некоторой другой функцией  путем разложения в ряд f(x) и сохранения членов, содержащих вторые производные:
путем разложения в ряд f(x) и сохранения членов, содержащих вторые производные: 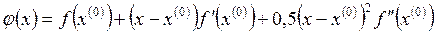 (1).
(1).
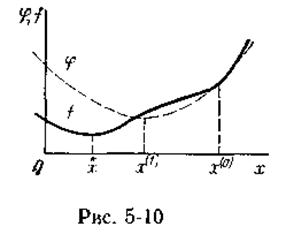 Такая аппроксимация соответствует замене исходной функции f(x) параболой
Такая аппроксимация соответствует замене исходной функции f(x) параболой  , совпадающей в точке
, совпадающей в точке 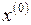 по значениям первой и второй производных (рис. 5-10). Если обозначить через
по значениям первой и второй производных (рис. 5-10). Если обозначить через 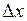 величину отклонения от
величину отклонения от 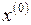 , то вместо (1) можно записать
, то вместо (1) можно записать  (2).
(2).
Найдем такое значение приращения 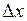 , которое обращает в минимум
, которое обращает в минимум 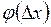 . Для этого приравняем нулю производную от (2):
. Для этого приравняем нулю производную от (2):  , откуда
, откуда 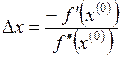 . Следовательно, точку
. Следовательно, точку 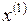 экстремума
экстремума  можно найти из условия
можно найти из условия  .
.
Если в этой точке производная  существенно отличается от нуля, то эту точку следует рассматривать как исходную и повторить вычисления. В общем виде рекуррентное выражение итерационного процесса можно представить как
существенно отличается от нуля, то эту точку следует рассматривать как исходную и повторить вычисления. В общем виде рекуррентное выражение итерационного процесса можно представить как 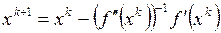 .
.
Таким образом, суть метода заключается в том, что исходная функция заменяется полиномом второй степени – параболой – и затем отыскивается ее минимум. В новой точке аппроксимация повторяется, отыскивается ее минимум и т. д.
Аналогично функцию двух переменных F(х1, х2), которая аппроксимируется разложением в ряд Тейлора, можно представить как 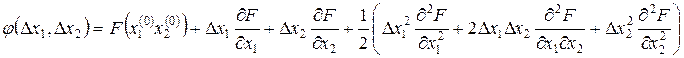 (3).
(3).
Градиент этой новой функции в точке ее экстремума равен нулю:
23.2 Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе
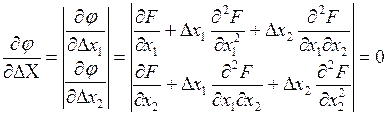 (4). Решая эту систему относительно
(4). Решая эту систему относительно 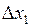 и
и 
 (5), находим точку экстремума, а следовательно, и точку нового приближения х1:
(5), находим точку экстремума, а следовательно, и точку нового приближения х1: 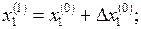
 (6).
(6).
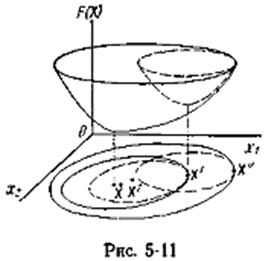
Геом-я интерпретация рассмотренного случая представлена на рис. 5-11. Истинная зависимость F(x) заменена параболоидом  , линии равного уровня которого в проекции на плоскость осей x1 и х2 - эллипсы. Решение системы (4) позволяет найти центр эллипсов х1, а затем в этой точке повторить аппроксимацию и найти точку х2 и т. д.
, линии равного уровня которого в проекции на плоскость осей x1 и х2 - эллипсы. Решение системы (4) позволяет найти центр эллипсов х1, а затем в этой точке повторить аппроксимацию и найти точку х2 и т. д.
Выражения (3–6) соответствуют общему случаю минимизации функции многих переменных F(x). В векторно – матричной форме эти выражения приобретают вид 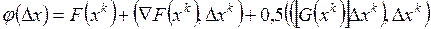 ;
; 

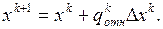
Функция 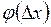 позволяет найти приближенное значение исходной функции F(x) и совпадает с ней лишь в точке разложения х°. В первом из этих выражений второй и третий члены – скалярные произведения векторов, отделенных друг от друга запятой. Через [G(x)] обозначена матрица вторых частных производных:
позволяет найти приближенное значение исходной функции F(x) и совпадает с ней лишь в точке разложения х°. В первом из этих выражений второй и третий члены – скалярные произведения векторов, отделенных друг от друга запятой. Через [G(x)] обозначена матрица вторых частных производных:  , называемая матрицей Гессе. Эта матрица всегда симметрична. Вектор F'(x) есть вектор первых частных производных целевой функции и, следовательно, это есть градиент
, называемая матрицей Гессе. Эта матрица всегда симметрична. Вектор F'(x) есть вектор первых частных производных целевой функции и, следовательно, это есть градиент 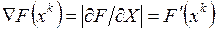 .
.
24.1 Комплексная оптимизация режимов энергосистемы
В общем случае для получения решения приходится применять современные методы нелинейного программирования. Рассмотрим применение для этой задачи метода приведенного градиента.
Любая задача нелинейного математического программирования может быть записана в следующей форме. Имеется функция многих переменных 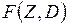 .
.
Компоненты Z являются искомыми параметрами режима, a D включает известную исходную информацию о состоянии системы, тогда min F(Z, D) совпадает с min F(Z). Необходимо по Z минимизировать функцию 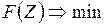 при ограничениях
при ограничениях 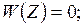
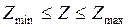 .
.
При использовании метода приведенного градиента компоненты вектора параметров режима системы Z разделяются на два подмножества X и Y: Y включает независимые переменные, т. е. те параметры, которые в системе могут регулироваться, на которые можно воздействовать, используя определенные средства управления; X включает зависимые параметры режима, т. е. те, которые могут быть вычислены по параметру Y, тогда  , отсюда
, отсюда 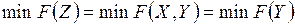 , а ограничения принимают вид:
, а ограничения принимают вид:
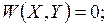

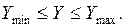
Связи между независимыми Y и зависимыми X переменными, как правило, неявные. Поэтому задача минимизации функции (6-G7) решается по многошаговой схеме.
Деление параметров режима Z на два подмножества X и Y понижает размерность задачи и, следовательно, облегчает вычислительный процесс. Действительно, если Z имеет n переменных, а X имеет m переменных, то обычно размерность задачи p<<n.
Рассмотрим основные положения решения задачи комплексной оптимизации методом приведенного градиента. ЭС состоит из i = 1, 2,..., М обобщенных и отдельных узлов и имеются только тепловые станции. Параметры режима:  ,
, 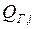 – активные и реактивные мощности генераторных узлов;
– активные и реактивные мощности генераторных узлов; 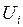 ,
, 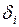 – модули напряжений и фазовые углы в узлах системы. Известны активные и реактивные нагрузки в узлах, причем они не зависят от напряжений и частоты системы. Требуется определить оптимальное распределение нагрузки по условию минимума расхода условного топлива системы.
– модули напряжений и фазовые углы в узлах системы. Известны активные и реактивные нагрузки в узлах, причем они не зависят от напряжений и частоты системы. Требуется определить оптимальное распределение нагрузки по условию минимума расхода условного топлива системы.
24.2 Комплексная оптимизация режимов энергосистемы
1. Уравнение цели 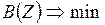 .
.
Вектор параметров Z разделяется на вектор независимых переменных  и зависимых переменных
и зависимых переменных 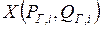
Тогда можно записать 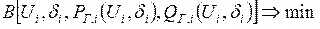 .
.
2. Уравнения связи включают:
– эквивалентные характеристики генераторных узлов вида  , где
, где 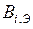 – эквивалентный расход условного топлива;
– эквивалентный расход условного топлива;
– связи между параметрами X и Y, которые имеют вид Y(Х);
3. Уравнения ограничений, которые задаются в виде неравенств
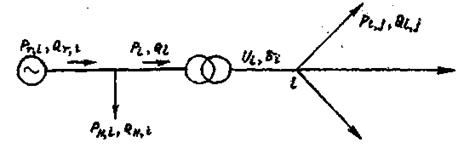
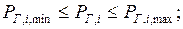

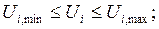

Задаются также балансовые ограничения по активным и реактивным мощностям в виде системы уравнений установившегося режима (рис.).
Для каждого узла небаланс по мощности равен: 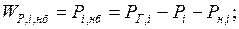
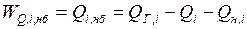 , где
, где 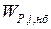 и
и  – функция небаланса по активной и реактивной мощностям.
– функция небаланса по активной и реактивной мощностям.
Когда в стационарном режиме в узлах системы имеется баланс, то  ,
, 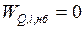 . Если в стационарном режиме изменить независимые переменные
. Если в стационарном режиме изменить независимые переменные 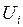 ,
, 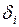 , то появится небаланс и
, то появится небаланс и 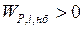 ,
, 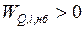 . Меняя
. Меняя  ,
, 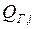 , можно получить новый допустимый стационарный режим для новых значений
, можно получить новый допустимый стационарный режим для новых значений 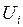 ,
, 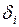 . Задача и будет заключаться в том, чтобы найти такое решение уравнений установившегося режима, при котором
. Задача и будет заключаться в том, чтобы найти такое решение уравнений установившегося режима, при котором  .
.
4. Вычисление приведенного градиента. Решение считается оптимальным, если модуль градиент - вектора  функции В (Х, Y) будет меньше заданного малого значения, т. е.
функции В (Х, Y) будет меньше заданного малого значения, т. е. 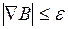 .
.
1. Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы
2. Применение метода множителей Лагранжа при решении задач оптимизации в ЭЭ
3. Опт-е распределение перетоков мощности в замкнутых контурах эл. сети
4. Прим-ие м-да множителей Л. для опт-ии перетоков мощности в эл. сети
5. Оптимизация распределения перетоков мощности сложной эл. сети
6. Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительные приросты ТЭС
7. Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Структурная схема алгоритма
8. Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь P. Физический смысл равенства относительных приростов
9. Определение опт. распределения нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относит. приросты ТЭС и ГЭС
10. Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме
11. Оптимальное распределение нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения
12. Оптимальное распределение нагрузки при переменном напоре ГЭС
13. Оптимальное распределение нагрузки между агрегатами электростанций. Оптимальная последовательность включения агрегатов электростанций
14. Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования. Основные определения
15. Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике
16. Применение метода наискорейшего спуска при решении задач опт-ии в ЭЭ
17. Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике
18. Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода
19. Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод + метод наискорейшего спуска
20. Применение градиентных методов оптимизации в электроэнергетике. Метод проектирования градиента
21. Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент
22. Учет ограничений в форме неравенств при решении задач оптимизации в электроэнергетике. Метод штрафных функций
23. Оптимизация режима электроэнергетической системы методом Ньютона. Матрица Гессе. Геометрическая интерпретация аппроксимации ЦФ
24. Комплексная оптимизация режимов энергосистемы
Поиск по сайту: