 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Для студентов IV курса групп ИП (7-ой семестр)
1) Найти расстояние от точки  до гиперплоскости
до гиперплоскости  .
.
2) Найти расстояние от точки  до прямой
до прямой  .
.
3) Найти расстояние от точки  до конуса
до конуса  .
.
4) Пусть  - точка локального экстремума в конечномерной гладкой экстремальной задаче с равенствами
- точка локального экстремума в конечномерной гладкой экстремальной задаче с равенствами 
 . Линейно зависима или линейно независима система векторов
. Линейно зависима или линейно независима система векторов  ?
?
5) Сколько нормалей можно провести из точки  к эллипсу
к эллипсу  ?
?
6) Докажите, что собственная функция выпукла тогда и только тогда, когда она удовлетворяет неравенству Иенсена.
7) Выяснить, являются ли выпуклыми функции одной переменной:
а)  ,
,
б) 
в)  ,
,
г)  .
.
8) Является ли выпуклой функция двух переменных
 ?
?
9) Доказать выпуклость следующих функций нескольких переменных и найти субдифференциалы этих функций:
а)  ,
,
б) 
в)  ,
,
г)  .
.
10) Доказать, что если собственная выпуклая функция  дифференцируема в точке
дифференцируема в точке  , то
, то  .
.
11) Найти субдифференциалы выпуклых функций одной переменной:
а) 
б)  ,
,
в)  .
.
12) Решить выпуклые задачи без ограничений:
а)  ,
,
б)  ,
,
в) 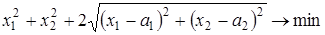 .
.
13) Доказать, что в выпуклой задаче локальный минимум является глобальным.
14) Применяя метод искусственного базиса, решить задачу линейного программирования в канонической форме:

15) Решить транспортную задачу с заданной платежной матрицей:
| b1=11 | b2=2 | b3=6 | b4=7 | |
| a1=7 | ||||
| a2=8 | ||||
| a3=5 | ||||
| a4=6 |
16) Найдите производные Фреше следующих отображений:
а)  ,
,
б)  ,
,
в)  ,
,
г)  ,
,
д)  ,
,
е)  ,
,
ж) 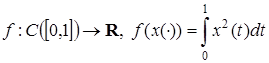 ,
,
з)  ,
,
и)  ,
,
к) 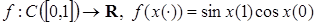 .
.
17) Решить задачу классического вариационного исчисления, сведя ее к задаче оптимального управления:
а)  ,
,
б)  .
.
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ К ЭКЗАМЕНУ ПО КУРСУ “МЕТОДЫ ОПТИМИЗАЦИИ”
Поиск по сайту: