АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка оптимальной задачи для каскада идеального перемешивания

Читайте также:
  1. I Психологические принципы, задачи и функции социальной работы
  2. I. 1.1. Пример разработки модели задачи технического контроля
  3. I. 1.2. Общая постановка задачи линейного программирования
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  6. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  7. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  8. I. Ситуационные задачи и тестовые задания.
  9. I. Цель и задачи дисциплины
  10. I.5.3. Подготовка данных для задачи линейного программирования
  11. I.5.4. Решение задачи линейного программирования
  12. I.5.5. Просмотр и анализ результатов решения задачи

Необходимо найти значение Топт и τопт, обеспечивающие экстремум критерия оптимальности при наличии ограничений в виде гидродинамических уравнений при условии :

 

 

Аналитический метод нахождения оптимального времени пребывания частиц τопт и Топт.

Для реакции типа А→Р→S найдем состав смеси на выходе реактора идеального смешения.

Аналитические выражения для скоростей образования реагентов А и Р имеют вид:

(5)
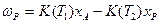
(6)

Стационарный режим определяется системой гидродинамических уравнений (при t1=t2)::

(7)
(8)

в результате решения которой находим:

(9)
(10)

В частном случае из уравнения (10) получим:

(11)

Критерием оптимальности является максимальная концентрация (степень превращения) продукта Р на выходе реактора. Для критерия оптимальности:

(12)

где K(T1), K(T2) - - константы скорости реакции;

t - время пребывания частиц в реакторе;

R – универсальная газовая постоянная;

T1 – температура реагента А;

T2 – температура реагента P.

Дифференцируем выражение (12) по t и T, находим систему уравнений, определяющих оптимальные условия реакции:

(13)
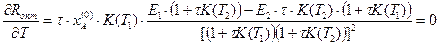
(14)

Эта система эквивалентна следующей системе:

(15)
(16)

Из уравнения (15) выводим формулу для нахождения оптимального времени пребывания в реакторе при заданном значении температуры:

(17)

Подставляя выражение (17) в уравнение (16), имеем:

(18)

Решение уравнения (16) для заданного времени пребывания имеет вид:

(19)

Отсутствие абсолютного экстремума у критерия оптимальности (12) означает, что его наибольшее значение следует искать на границе области допустимых значений переменных T и τ.

Для определения оптимальной температуры необходимо решить уравнение (16). Подставим выражение (17) в соотношение для критерия оптимальности (12). В результате получим:

(20)

Если заданы ограничения на температуру , то оптимальная температура будет:

при

при


1 | 2 | 3 | 4 | 5 |

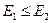
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)