Постановка задачи векторной оптимизации. Оптимальность по Парето

Тема 9 ВЕКТОРНАЯ ОПТИМИЗАЦИЯ

Методические указания

Постановка задачи векторной оптимизации. Оптимальность по Парето.

Эффективность функционирования экономической системы оценивается, как правило, несколькими критериями. Математической формой критерия эффективности в оптимизационных экономико-математических задачах является целевая функция.

Пусть имеется критериев, которые можно записать в виде целевых функций , где . Поскольку , то для простоты в дальнейшем будем предполагать, что все целевые функции максимизируются. Задача многокритериальной оптимизации в этом случае запишется

(1)

; (2)

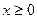. (3)

Если точки максимума 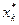, определенные при решении задач по каждому критерию не совпадают, то решение задачи (1)-(3) может быть только компромиссным. В области допустимых значений задачи находится область компромиссов. При перемещении из одной точки области компромиссов в другую, невозможно одновременное улучшение всех критериев. Принадлежащие области компромиссов планы называются эффективными или оптимальными по Парето (по имени итальянского экономиста, впервые сформулировавшего проблему многокритериальной оптимизации и принцип оптимальности).

План 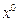оптимален по Парето, если он допустим, и не существует другого плана для которого

,

и хотя бы для одного критерия выполняется строгое неравенство.

К задачам векторной оптимизации приходят в следующих случаях:

1. Качество моделируемого процесса нужно оценить с точки зрения нескольких показателей. Это могут быть прибыль, себестоимость, рентабельность и т.д.

2. Моделируемые процесс представляет собой составляющую нескольких процессов (частей), и каждая из этих частей имеет свой критерий качества.

3. Моделируемые процесс расчленяется на несколько шагов и на каждом шаге его качество определяется своей функцией. (Например, на отдельных временных промежутках)

При разработке методов решения многокритериальных задач приходится решать ряд специфических проблем.

1. Проблема нормализации возникает наиболее часто. Отдельные критерии как правило имеют различные единицы и масштабы измерения, что делает невозможным их непосредственное сравнение. К единому и безразмерному виду критерии приводятся посредством операции нормирования. Наиболее распространенными способами нормирования является замена абсолютных значений критериев их относительными величинами

,

или относительными значениями отклонений от оптимальных значений критериев

.

2. Проблема учета приоритета критериев встает, если критерии имеют различную значимость. В этом случае необходимо найти математическое определение приоритета и степень его влияния на решение задачи.

3. Проблема определения области компромисса возникает при решении многомерных нелинейных задач, поэтому для их решения необходимо применять методы, гарантирующие эффективное решение.

Методы решения задач многокритериальной оптимизации можно подразделить на четыре группы:

– методы, основанные на свертывании критериев;

– методы, использующие ограничения на критерии;

– методы целевого программирования;

– методы, основанные на отыскании компромиссного решения.

Вместо исходной многокритериальной задачи в соответствии с выбранным методом, формируется замещающая задача. В состав замещающей задачи входит один критерий, а к исходной системе ограничений добавляется одно или несколько дополнительных ограничений. Решение замещающей задачи называется субоптимальным.

Поиск по сайту: