Безусловная минимизация функций одной переменной

Будем решать задачу

(3.1)

Можно выделить три основных подхода к ее решению.

Первый подход основан на численном решении уравнения

Если целевая функция имеет только один минимум и является выпуклой, то решение уравнения (3.2) даст единственное решение задачи (3.1). В противном случае, корни (3.2) дадут все экстремальные точки и точки перегиба целевой функции. Та точка, в которой значение целевой функции наименьшее, будет решением задачи (3.1). На этом подходе основан метод Ньютона.

Второй подход предполагает выделение на оси O x интервала [ a,b ], в котором заключен минимум целевой функции и последовательное уменьшение в процессе вычислений длины этого интервала до требуемой точности . Представителем данного класса методов является метод «золотого сечения».

Наконец, третий подход основан на локальной аппроксимации целевой функции квадратичными или кубическими многочленами. Это позволяет на каждом шаге алгоритма аппроксимировать минимум целевой функции минимумом многочлена. В процессе вычислений каждая последующая аппроксимация строится с использованием очередной точки приближения минимума целевой функции, что позволяет последовательно продвигаться к этому минимуму. Примером подобных методов является метод квадратичной аппроксимации.

3.1 Метод Ньютона. Для решения нелинейного уравнения (3.2) воспользуемся методом Ньютона. Выбрав начальное приближение , каждое последующее приближение будем искать по формуле:

Таким образом, метод Ньютона является градиентным методом второго порядка. Итерационный процесс, описываемый (3.3), завершают, когда два последовательно найденных приближения отличаются друг от друга менее чем на заранее заданную величину :

или когда значение первой производной станет достаточно малым (напомним, что в точке минимума оно становится равным нулю):

На практике же «для надежности» лучше требовать одновременного выполнения обоих условий (3.4) и (3.5).

Алгоритм 3.1 метода Ньютона

1. Задать начальное приближение , параметры, управляющие завершением итерационного процесса и .

2. .

3. Выполнять цикл…

3.1. Вычислить в точке ;

3.2. ;

3.3. .

…до тех пор, пока или .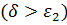

4. Вывести результат – .

5. Завершить работу.

Сходимость метода Ньютона зависит от выбора начального приближения. Можно доказать, что если F(x) дважды непрерывно дифференцируема, 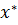- точка минимума этой функции, в которой , то всегда найдется окрестность точки 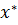такая, что приближения, начатые из произвольной точки , лежащей в этой окрестности, сверхлинейно сходятся к 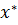, то есть для любого и некоторого (зависящего от q) C выполняется неравенство . Более того, при выполнении определенных дополнительных условий, в некоторой окрестности минимума может иметь место квадратичная сходимость метода Ньютона: .

Таким образом, главным достоинством метода Ньютона является его быстрая сходимость.

Применимость метода Ньютона ограничена требованием, чтобы целевая функция была дважды дифференцируема в окрестности ее минимума, в которой осуществляется поиск решения.

Основной недостаток метода Ньютона заключается в том, что при неудачном выборе начального приближения этот метод может расходиться. Кроме того, на каждом шаге требуются вычисления первой и второй производной целевой функции. Если аналитические выражения для первой и второй производных неизвестны, численный расчет производных может оказаться трудоемким и вносить в процесс вычислений непредсказуемую погрешность.

3.2 Метод «золотого сечения». Метод «золотого сечения» является методом нулевого порядка. Он может быть разбит на два последовательных этапа:

1. Локализация минимума целевой функции.

2. Последовательное сужение интервала локализации.

Для локализации интервала, на котором располагается минимум целевой функции воспользуемся следующим критерием:

Если для унимодальной функции одной переменной F(x) удалось найти такие три точки

, (3.6)

что

и , (3.7)

то точка 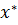, в которой достигается минимум функции F(x) лежит в интервале (

Из сказанного не следует обратное. Нельзя утверждать, что если точка 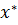, в которой достигается минимум функции F(x) лежит в интервале (, то для любой точки будут выполняться неравенства (3.7). Чтобы убедиться, что минимум целевой функции находится в интервале надо не просто взять произвольную точку и проверить выполнение (3.7), а необходимо найти (построить) такую точку , в которой будут выполняться эти неравенства.

Рассмотрим алгоритм локализации минимума унимодальной функции одной переменной, основанный на использовании приведенного выше критерия.

Алгоритм 3.2 локализации минимума

1. Задать начальную точку , шаг поиска , коэффициент (для метода «золотого сечения ), точность вычисления минимума , предельное число шагов поиска N.

2. Пока выполнять // ищем точку

2.1. .

2.2. Если , то выйти из цикла

2.3. h:= – h.

2.4. .

2.5. Если , то выйти из цикла

2.6. .

3. Если , то вывести результат поиска минимума и завершить работу.

4. Для r от 1 до N с шагом +1 выполнять цикл // поиск

4.1.

4.2. .

4.3. Если , то выйти из цикла

4.4.

5. Если r=N, сообщить о невозможности локализации минимума и завершить аварийно работу.

6. .

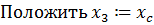7. Если , то положить

иначе положить

8. Завершить работу

Алгоритм 3.1 обеспечивает локализацию минимума унимодальной целевой функции на интервале . Кроме того, всегда будет выполняться следующее соотношение:

Если в качестве взять корень уравнения , равный приблизительно 1,618, то отрезок будет разделен на две неравные части в пропорции так называемого «золотого сечения». При этом весь отрезок так относится к его большей части, как сама большая часть относится к меньшей. Разделив таким образом интервал локализации минимума, в дальнейшем получают наиболее быстрое сужение этого интервала в случае, когда число итераций соответствующего алгоритма стремится к бесконечному. Сам же алгоритм последовательного сужения интервала локализации при называется алгоритмом «золотого сечения».

Идея алгоритма метода «золотого сечения» заключается в следующем. В качестве исходных имеются 3 точки , удовлетворяющие условиям (3.6) и (3.7), причем . Выберем точку , лежащую симметрично точке относительно середины отрезка : . После этого следует рассмотреть два варианта взаимного расположения точек и : и вместе с двумя вариантами соотношения значений целевой функции в этих точках: и . Таким образом, всего необходимо проанализировать 4 варианта, которые показаны на рис. 3.1 – 3.4. В каждом из 4 вариантов можно определить новые точки и , а также точку , которые будут определять более узкий интервал локализации, удовлетворяя условиям (3.6) и (3.7).

Алгоритм 3.2а метода «золотого сечения»

1. Взять точки такие, что , и
. Задать точность нахождения минимума и предельное число итераций N.

2. Вычислить

3. Найти положение точки симметрично относительно середины интервала : .

4. Для r от 1 до N с шагом +1 выполнять цикл

4.1. Вычислить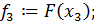

4.2. Если , то

4.2.1. Если 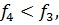то

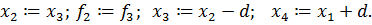
иначе

иначе

4.2.2. Если 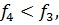то

иначе

4.3. Положить

4.4. Если , выйти из цикла.

5. Если r=N, сообщить о невозможности нахождения минимума и завершить аварийно работу.

6. Положить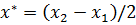

7. Завершить работу.

Следует предостеречь от вычисления в цикле новых значений по простой формуле , которая использовалась в п.2 данного алгоритма при однократном вычислении. Использование этой формулы в цикле приводит к очень быстрому накоплению ошибок, нарушению пропорций между длинами отрезков и, в результате, даже к зацикливанию программы. Введенный дополнительно к этому пересчет на каждой итерации положения точки позволяет избежать такого накопления ошибок.

Достоинства метода «золотого сечения» - отсутствие необходимости вычисления производных, гарантированная сходимость в том случае, если на первом шаге удалось локализовать один минимум целевой функции. Основной недостаток – относительно медленная сходимость (по сравнению, например, с методом Ньютона).

3.3 Метод квадратичной аппроксимации. Данный метод также является методом нулевого порядка и не требует вычисления производных целевой функции.

Данный метод основан на локальной аппроксимации целевой функции квадратичной функцией. Для этого на оси O x выбирают три точки . Через эти точки на графике целевой функции проводят квадратичную параболу . Для этого определяют коэффициенты a,b,c из системы уравнений:

(3.9)

Получаем:

В качестве очередного приближения минимума функции рассматривают минимум параболы – точку

Затем из трех точек отбрасываем точку с наибольшим значением целевой функции. К оставшимся двум точкам добавляем и получаем новую последовательность из трех точек на оси O x. Если решение не достигнуто (разность между наибольшим и наименьшим значениями целевой функции в этих трех точках больше наперед заданного ), то переходят к построению новой квадратичной параболы, нахождению ее минимума и т.д.

Метод квадратичной аппроксимации гарантированно работает для унимодальных выпуклых целевых функций. На практике начальные точки выбирают не произвольным образом, а так, чтобы они локализовывали минимум целевой функции. Для этого можно использовать алгоритм 3.2, взяв . Далее, как описано выше, после нахождения точки , пытаются отбросить точку с наибольшим значением целевой функции. Однако, если оставшиеся три точки не локализуют минимум (то есть ни в какой комбинации не удовлетворяют условиям (3.6) и (3.7)), то вместо точки с наибольшим значением целевой функции следует отбросить точку со следующим по величине значением этой функции.

Алгоритм 3.3 метода квадратичной аппроксимации

1. Взять точки такие, что , и
. Задать точность нахождения минимума и предельное число итераций N.

2. Вычислить

3. Для r от 1 до N с шагом +1 выполнять цикл

3.1. Вычислить a, b, c по формулам (3.10), (3.11), (3.12).

3.2. Положить . Вычислить

3.3. Упорядочить точки и соответствующие им значения в порядке неубывания значений целевой функции: .

3.4. Если три первые точки не локализуют минимум ( или , то

Поменять местами точки и :

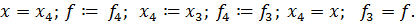
Если три первые точки снова не локализуют минимум ( или , то

Поменять местами точки и : и выдать предупреждение о потере локализации минимума

3.5. Если , выйти из цикла

4. Если r=N, сообщить о невозможности нахождения минимума и завершить аварийно работу.

5. Положить

6. Завершить работу.

Метод квадратичной аппроксимации полезен для решения задачи одномерного поиска вдоль заданного направления, возникающей при реализации различных методов минимизации функций n переменных. Метод гарантированно работает для унимодальных выпуклых функций (по крайней мере, унимодальных на участке, на котором первоначально локализован минимум).

4. Безусловная минимизация функций n переменных

Рассмотрим две основные группы методов безусловной минимизации функций n переменных:

(4.1)

Первую группу составляют методы прямого поиска (методы нулевого порядка). Их главное достоинство – отсутствие требований к дифференцируемости целевой функции. Эти методы удобны, когда не могут быть получены аналитические выражения для производных целевой функции, и эти производные приходится вычислять с помощью конечных разностей. Наконец, многие методы прямого поиска (например, локальных вариаций или Хука-Дживса), не требуют выпуклости целевой функции. В случае многоэкстремальных задач они позволяют найти локальный экстремум, ближайший к начальной точке поиска. Главный недостаток методов прямого поиска – медленная сходимость.

В отличие от методов прямого поиска, градиентные методы первого и второго порядков, составляющие вторую группу, отличаются быстрой сходиимостью. Однако, они не гарантируют сходимость для невыпуклых и, тем более, многоэкстремальных функций. Градиентные методы требуют дифференцируемости целевой функции один или два раза, в зависимости от порядка метода. Производные приходится вычислять на каждой итерации градиентного метода.

4.1 Метод покоординатного спуска. Данный метод нулевого порядка является одним из самых простых и интуитивно понятных эмпирических методов безусловной минимизации функций n переменных. В пространстве выбирается начальная точка . Далее, на каждой итерации, последовательно выполняется одномерный поиск минимума функции по направлению каждой из координатных осей :

Выполнив одномерный поиск в направлении i -й координатной оси, перемещаем начальную точку поиска в точку, где функция достигает минимального значения вдоль этой оси:

Проведя поиск вдоль всех координатных осей, сравниваем расстояние между начальной точкой и результирующей точкой c заранее заданной величиной . Если это расстояние больше , начальную точку перемещают в результирующую: 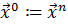и процедуру одномерного поиска повторяют последовательно вдоль всех координатных осей (см. рис. 4.1).

Алгоритм 4.1 метода покоординатного спуска

1. Задать начальную точку , значение , предельное число шагов поиска N.

2. Положить .

3. Для r от 1 до N с шагом +1 выполнять цикл

3.1. Для i от 1 до n с шагом +1 выполнять цикл

3.1.1. Решить задачу

3.1.2. Положить

3.2. Если , то выйти из цикла

3.3. Положить .

4. Если , то вывести предупреждение, что минимум не достигнут

5. Положить .

6. Завершить работу

Для одномерного поиска на шаге 3.1.1 чаще всего используют метод квадратичной аппроксимации или метод «золотого сечения».

При своей простоте метод покоординатного спуска не лишен недостатков. Во-первых, минимизация невыпуклых функций, даже унимодальных, может привести к задачам одномерной минимизации многоэкстремальных функций (рис. 4.2). Во-вторых, в случае, когда линии равного уровня (при – поверхности равного уровня) целевой функции вытянуты не вдоль координатных осей (образуют овраг), алгоритм не приводит к нахождению минимума (рис. 4.3).

4.2. Метод локальных вариаций. Этот метод по своей идее напоминает метод покоординатного спуска, однако одномерный поиск заменен пробными шагами вдоль координатных осей. Длины шагов уменьшаются при приближении к минимуму целевой функции.

В основе метода локальных вариаций лежит алгоритм покоординатного поиска. Пусть вектор задает величины пробных шагов вдоль каждой координатной оси. Последовательно для всех координат 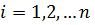делаем из текущей точки поиска пробные шаги, сначала в положительном направлении . Если этот шаг оказался удачен (), то текущую точку перемещают в найденную точку и переходят к следующей координате. Если шаг оказался неудачен, направление поиска меняют на противоположное: . а затем, если значение целевой функции улучшить не удалось, в противоположном. Если этот шаг оказался удачен (), то текущую точку перемещают в найденную точку . Если поиск не дал результатов ни для одного из направлений, шаг поиска уменьшают и процедуру повторяют последовательно для всех координат. Если шаг из-за уменьшения стал меньше заданного, поиск прекращают (рис. 4.2).

Алгоритм 4.2 метода локальных вариаций

1. Задать начальную точку , минимальное значение шага вдоль первой координатной оси , длины шагов вдоль каждой координатной оси , предельное число шагов поиска N.

2. Положить

3. Для r от 1 до N с шагом +1 выполнять цикл

3.1. Выполнить покоординатный поиск из точки с шагом с результатом в точке .

3.2. Если результат поиска совпадает с исходной точкой (то есть ), то Если , выйти из цикла.

4. Если , то вывести предупреждение, что минимум не достигнут за заданное число шагов

5. Положить .

6. Завершить работу.

В процессе покоординатного поиска сначала выполняется пробный шаг вдоль первой координаты в положительном направлении . Если значение целевой функции улучшилось, полученная точка фиксируется, и мы переходим к следующей координате. Если значение функции уменьшить не удалось, делают шаг в противоположном направлении . Если после этого шага значение целевой функции улучшилось, то полученная точка фиксируется, и мы переходим к следующей координате. В противном случае, текущая точка остается на месте и осуществляется переход к следующей координате. Эта процедура последовательно выполнятся по всем координатам (алгоритм 4.2а).

Алгоритм 4.2а покоординатного поиска
из точки с шагом с результатом в точке .

1. Положить ).

2. Для i от 1 до n с шагом +1 выполнять цикл

2.1. . Вычислить

2.2. Если шаг удачен ( то ;

Иначе . Вычислить

Если шаг удачен ( то ;

3. Завершить работу.

Данный алгоритм сходится несколько медленнее, чем метод покоординатного спуска, однако, применим для невыпуклых и даже многоэкстремальных функций, позволяя найти один из локальных минимумов многоэкстремальной функции (в зависимости от выбора начальной точки). В то же время для функций, линии (поверхности) уровня которых вытянуты в виде оврагов на вдоль одной из координатных осей, этот метод, как и метод покоординатного спуска, практически неработоспособен.

4.3. Метод Хука-Дживса. Данный метод является одним из лучших методов прямого поиска. Он, в частности, сохраняет работоспособность для функций, у которых линии (поверхности) равного уровня вытянуты не вдоль координатных осей. Метод Хука-Дживса не требует выпуклости целевых функций. Данный метод может также применяться для минимизации многоэкстремальных функций, приводя, при выборе различных начальных точек, к различным локальным минимумам таких функций.

В основе метода Хука-Дживса лежит идея метода локальных вариаций. Однако, в методе Хука-Дживса направления поиска не зафиксированы вдоль координатных осей. Алгоритм стремится построить направление поиска, приближающееся к направлению наискорейшего убывания целевой функции. Таким образом, встретившись с «оврагом» целевой функции, метод Хука-Дживса стремится вытянуть направление поиска вдоль дна этого «оврага». Кроме этого, размер шага вдоль перспективного направления также может изменяться в зависимости от поведения целевой функции.

Алгоритм 4.3 метода Хука-Дживса

1. Задать начальную точку , минимальное значение шага вдоль первой координатной оси , длины шагов вдоль каждой координатной оси , предельное число итераций N.

2. Положить Положить )

3. Выполнять для r от 1 до N с шагом +1

3.1. Выполнять бесконечный цикл

3.1.1. Выполнить покоординатный поиск из точки с шагом с результатом в точке (алгоритм 4.2а).

3.1.2. Если результат поиска не совпадает с исходной точкой (то есть ), то положить и выйти из цикла.
Иначе

3.1.2.1.

3.1.2.2. Если , пожить в качестве результата и завершить работу программы.

3.2. Выполнять до тех пор…

3.2.1. Экстраполировать направление к минимуму, положив 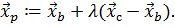Как правило, используют фиксированное значение .

3.2.2. Выполнить покоординатный поиск из точки с шагом с результатом в точке (алгоритм 4.2а). Положить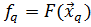

3.2.3. Положить 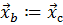и ; положить .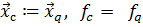

3.2 …пока новые значения

4. Вывести предупреждение, что минимум не достигнут за заданное число шагов.

5. Завершить работу.

Шаг 3.1 в литературе называется «исследующим поиском». Он заключается в том, чтобы путем покоординатного поиска вокруг базовой точки найти новую точку , в которой значение целевой функции лучше. Если шаг 3.1 неудачен, шаг поиска уменьшают, пока он не станет меньше наперед заданного. В последнем случае поиск завершают.

Шаг 3.2 часто называют «поиск по образцу». В том случае, если шаг 3.1 оказался удачным, новую перспективную точку пытаются построить вдоль прямой, соединяющей две предыдущие точки и 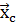. Обычно такую экстраполяцию выполняют с постоянным коэффициентом . (В литературе встречаются указания на возможность подбора других значений этого параметра или вообще на выполнение одномерного поиска вдоль прямой, соединяющей точки и 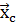). Далее, следует обратить внимание, что значение целевой функции в новой точке , полученной в результате экстраполяции, не анализируется, а из нее сразу осуществляется покоординатный поиск с результатом в точке Если покоординатный поиск не привел к нахождению точки, лучшей чем , то точка будет с ней совпадать. 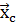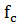Теперь, наконец, сравнивают значения целевой функции в прежней наилучшей точке и новой точке , полученной в результате «поиска по образцу» (в приведенном выше алгоритме до этого осуществляется переприсваивание и , и поэтому сравнивают уже не и 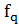, а, соответственно новые значения и 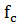. В случае, если поиск «по образцу» оказался удачен, его повторяют.

Во избежание зацикливания, общее число итераций алгоритма целесообразно ограничить.

4.4. Метод наискорейшего спуска. Этот метод, пожалуй, является наиболее простым градиентным методом, то есть методом, требующим вычисления производной целевой функции. Метод наискорейшего спуска относится к методам первого порядка, то есть требует возможности вычисления первой производной целевой функции в любой точке области допустимых значений варьируемых параметров.

Метод наискорейшего спуска предлагает, выбрав начальную точку, искать минимальное значение целевой функции путем одномерного поиска вдоль направления, противоположного градиенту этой функции. Действительно, направление градиента – это направление наиболее быстрого возрастания функции переменных, а противоположное ему направление – направление наиболее быстрого убывания. Однако свойство градиента является лишь локальным, поэтому для произвольной целевой функции однократная реализация процедуры такого одномерного поиска к нахождению минимума не приведет. Ее придется повторять в итерационном цикле, выбирая предыдущую точку одномерного минимума в качестве начальной для нового поиска (рис. 4.4). Итерации могут быть завершены по одному из двух критериев: когда значение градиента по модулю станет меньше некоторого наперед заданного значения (в минимуме оно равно нулю) или когда расстояние между двумя последовательно найденными одномерными минимумами станет меньше наперед заданного. Первый критерий плохо работает при продвижении к минимуму по очень пологой поверхности, где он может сработать вдали от минимума. Второй критерий, напротив, может остановить выполнение алгоритма при спуске к крутому минимуму вблизи от него, но в точке, где значение целевой функции еще весьма далеко от минимального. В приведенном алгоритме для завершения поиска требуется выполнение обоих критериев.

Алгоритм 4.4 метода наискорейшего спуска

1. Задать начальную точку , значения , , предельное число шагов поиска N.

2. Положить ;

3. Для r от 1 до N с шагом +1 выполнять цикл

3.1. Решить задачу

3.2. Положить ;

3.3. Если и , то выйти из цикла

3.4. Положить .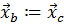

4. Если , то вывести предупреждение, что минимум не достигнут

5. Положить .

6. Завершить работу

Основным недостатком данного метода является то, что все направления поиска, которые строятся последовательно на всех итерациях, являются взаимно ортогональными. Действительно, в результате одномерного поиска минимума вдоль некоторого направления, мы находим точку, в которой скорость изменения целевой функции вдоль этого направления равна 0, то есть проекция градиента функции на это направление равна 0, что означает, что градиент ортогонален этому направлению. Так как в качестве следующего направления поиска выбирается направление, противоположное градиенту, получается, что это направление будет ортогонально предыдущему. В результате, в случае неудачного выбора начальной точки и овражистой целевой функции направления поиска могут «не улечься» на дно оврага и метод окажется неэффективным.

На самом деле, метод наискорейшего спуска, используя в качестве локального направления поиска антиградиент целевой функции, опирается на локальную аппроксимацию целевой функции квадратичной формой вида:

в случае, когда матрица квадратичной формы является диагональной, то есть линии (поверхности) уровня целевой функции представляют собой окружности (сферы, гиперсферы). Действительно, нетрудно видеть, что для такой целевой функции, какую бы начальную точку мы ни выбрали, направление антиградиента будет проходить через минимум этой функции. Это значит, что минимум будет найден всего за одну итерацию, реализующую процедуру одномерного поиска вдоль антиградиента. Для реальных целевых функций, чтобы найти минимум с заданной точностью, приходится выполнять несколько итераций, причем тем больше итераций, чем больше вытянуты линии (поверхности) уровня целевой функции. Говоря другими словами, если максимальное и минимальное значения собственных чисел матрицы Гессе целевой функции сильно различаются, метод наискорейшего спуска оказывается неэффективным (ранее мы показали это из соображений ортогональности направлений поиска).

4.5. Метод сопряженных градиентов. В отличие от метода наискорейшего спуска, данный метод подразумевает локальную аппроксимацию целевой функции не квадратичной формой с диагональной матрицей, а произвольной квадратичной формой с матрицей G. Отметим, что для квадратичной формы вида (4.2) ее матрица G совпадает с ее же матрицей Гессе H, полученной путем вычисления вторых производных:

По своей сути, метод сопряженных градиентов использует идею локальной аппроксимации произвольной целевой функции квадратичной формой, матрица которой совпадает с матрицей Гессе этой целевой функции в той точке, в которой локально выполняется аппроксимация.

Пусть в некоторой точке для целевой функции построена матрица Гессе Векторы , ,…, будем называть сопряженными относительно матрицы H, если выполняются соотношения:

, (4.4)

, (4.5)

Можно доказать, что для произвольной квадратичной формы с положительно определенной матрицей G, задав n сопряженных относительно G направлений , ,…, , можно найти минимум данной формы, последовательно выполнив n одномерных поисков вдоль этих направлений. При этом в качестве начальной точки для каждого последующего поиска берется результирующая точка предыдущего.

Метод сопряженных градиентов позволяет найти минимум квадратичной формы за одну итерацию, которая заключается в последовательной реализации n процедур одномерного поиска минимума вдоль n сопряженных направлений. В качестве первого направления берут направление, противоположное градиенту . Остальные n-1 направление поиска последовательно строят как взаимно сопряженные с и между собой относительно матрицы 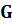(для квадратичной формы совпадает с ее матрицей Гессе H).

В случае произвольной функции таких итераций будет несколько. На каждой итерации аппроксимируют квадратичной формой, вычисляя матрицу Гессе H. На первой итерации матрица Гессе вычисляется в начальной точке поиска, на последующих итерациях – в точке, полученной в результате предыдущей итерации. Каждая итерация состоит из n процедур одномерного поиска вдоль направлений, сопряженных относительно матрицы H. Итерации повторяются до тех пор, пока не будет выполнен один из критериев завершения работы или оба этих критерия (см. алгоритм 4.4).

Существует несколько модификаций метода сопряженных градиентов, отличающихся способом последовательного вычисления сопряженных направлений. Одним из наиболее популярных является алгоритм Флетчера-Ривса, в котором сопряженные направления рассчитываются из следующих соображений.

Начнем с базовой точки поиска . В качестве первого направления поиска из базовой точки выберем

, (4.6)

В результате одномерного поиска вдоль этого направления найдем 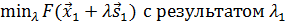и новую точку 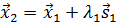. Новое направление поиска будем искать в виде

(4.7)

выбирая таким, чтобы направление было сопряжено с относительно матрицы H, вычисленной в точке :

, (4.8)

Для этого воспользуемся разложением градиента целевой функции вблизи точки 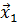и для значения градиента в точке получим следующее приближенное соотношение:

, (4.9)

отсюда

, (4.10)

транспонируя выражение (4.10) и домножая его справа на , получим:

(4.11)

Если целевая функция имеет непрерывные вторые производные, то матрица Гессе является симметричной, то есть и Отсюда

.(4.12)

Подставляя (4.12) в (4.8) получим:

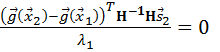(4.13)

Отсюда, с учетом (4.6) и (4.7) получаем:

.(4.14)

Раскрывая скобки, учтем, что в силу ортогональности векторов 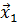и (см. пояснение в описании метода наискорейшего спуска), окончательно получаем:

, (4.15)

, (4.16)

В дальнейшем, имея на k -й итерации набор сопряженных направлений , ,…, , каждое следующее направление можно вычислить по формуле:

(4.17)

Это выражение можно переписать в рекурсивной форме:

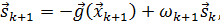(4.18)

где

, (4.19)

Такой способ выбора направлений используется в методе Флетчера-Ривса. Отметим, что в силу приближенности соотношения (4.9), мы получили приближенный способ расчета направлений, сопряженных относительно матрицы Гессе минимизируемой целевой функции. Существуют и другие методы сопряженных градиентов, в которых используются другие приближенные формулы. Так, в методе Полака-Райбера

(4.20)

Интересно, что и метод Флетчера-Ривса, и метод Полака-Райбера остаются методами первого порядка, не требуя непосредственного вычисления матрицы Гессе. Несмотря на то, что в методе сопряжённых градиентов используется информация только о линейной части приращения в точке, как и в методах градиентного спуска, метод сопряжённых градиентов позволяет решать квадратичные задачи за конечное число шагов. В то же время, вычислительная сложность этого метода не превышает сложности метода наискорейшего спуска при гораздо более высокой скорости сходимости. Сходимость метода Флетчера-Ривса строго доказана для целевых функций, удовлетворяющих определенным, не слишком строгим, условиям. Сходимость алгоритма Полака-Райбера доказана для выпуклых функций. На практике, однако, эти методы часто оказываются работоспособными и в тех случаях, когда эти условия сходимости не выполняются, причем алгоритм Полака-Райбера обычно показывает лучшие результаты. Методы сопряженных градиентов чувствительны к накоплению машинных ошибок.

Ниже приведен алгоритм метода Полака-Райбера.

Алгоритм 4.5 метода Полака-Райбера

1. Задать начальную точку , значения , , предельное число шагов поиска N.

2. Положить

3. Для r от 1 до N с шагом +1 выполнять цикл

3.1. Положить

3.2. Для i от 1 до n с шагом +1 выполнять цикл

3.2.1. Решить задачу

3.2.2. Положить ;

3.2.3. Положить

3.2.4. Положить ;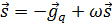

3.3. Если и , то выйти из цикла

3.4. Положить .

4. Если , то вывести предупреждение, что минимум не достигнут

5. Положить .

6. Завершить работу

4.6. Метод Пауэлла. Метод Пауэлла так же, как и метод сопряженных градиентов, основан на квадратичной аппроксимации целевой функции и использует поиск по взаимно сопряженным направлениям. Метод основывается на следующем свойстве квадратичной функции. Любая прямая, проходящая через точку минимума квадратичной формы пересекает под равными углами поверхности постоянного значения (в двумерном случае – линии равного уровня) этой квадратичной формы. Отсюда следует, что, если мы найдем два минимума и квадратичной формы , расположенных на двух параллельных прямых, направленных вдоль вектора , то минимум квадратичной формы следует искать вдоль направления . Это направление является сопряженным к относительно, матрицы 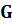. Действительно, градиент квадратичной функции в точке равен , а в точке , соответственно, . Как уже отмечалось, градиент, вычисленный в точке минимума, найденной в результате одномерного поиска по направлению , ортогонален . Так как точки и были получены в результате поиска минимума вдоль прямых, направленных вдоль вектора , то , откуда

. (4.21)

Алгоритм Пауэлла, используя соотношение (4.21) позволяет построить набор направлений, сопряженных относительно матрицы квадратичной формы, локально аппроксимирующей целевую функцию, не вычисляя производных, то есть относится к методам нулевого порядка.

Алгоритм 4.6 метода Пауэлла

1. Задать начальную точку , значение , предельное число шагов поиска N.

2. Положить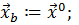

3. Для всех i от 1 до n положить , где - единичные векторы, направленные вдоль координатных осей; положить ;

4. Для r от 1 до N с шагом +1 выполнять цикл

4.1. Решить задачу ;

4.2. Положить ;

4.3. Для i от 1 до n с шагом +1 выполнять

4.3.1. Решить задачу ;

Поиск по сайту: