Условная минимизация

Вернемся к задаче однокритериальной параметрической оптимизации при наличии ограничений на варьируемые параметры:

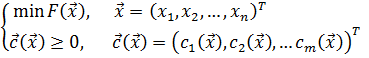(5.1)

Как и ранее, запись 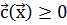будет означать, что все компоненты вектора 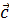должны удовлетворять неравенствам 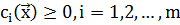, которые определяют область допустимых значений варьируемых параметров D. В настоящее время на практике чаще всего применяется один из трех подходов к решению подобных задач условной минимизации:

1. Сведение задачи условной минимизации к последовательности задач безусловной минимизации путем использования барьерных или штрафных функций (метод последовательной безусловной минимизации).

2. Применение метода скользящего допуска, позволяющего оперировать недопустимыми, но близкими к допустимым, векторами в пространстве поиска.

3. Применение методов случайного поиска.

Известны также методы, основанные на замене исходной задачи нелинейного программирования с ограничениями последовательностью аппроксимирующих задач, полученных путем линеаризации ограничений.

Самым простым способом сведения задачи условной минимизации к задаче минимизации без ограничений является замена целевой функции на новую функцию вида

(5.2)

Здесь P – достаточно большое положительное число, такое, что 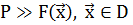. Очевидно, что безусловный минимум функции будет совпадать с условным минимумом функции .

В определенных случаях такой подход может привести к полезным результатам. Однако, в целом, он, чаще всего, не позволяет найти условный минимум целевой функции. Во-первых, этот метод не позволяет применять градиентные методы минимизации, такие как метод наискорейшего спуска и метод сопряженных градиентов, вследствие разрыва производных на границе области допустимых значений. Во-вторых, на границе области допустимых значений возникает «овраг», имеющий со стороны недопустимых значений бесконечную крутизну, что делает методы прямого поиска неэффективными. Наконец, выйдя на плато равных значений целевой функции за пределами области допустимых значений, методы прямого поиска вместо того, чтобы вернуться в эту область, могут просто остановиться, последовательно уменьшая шаги поиска и не находя направление уменьшения целевой функции. От указанных недостатков практически свободен метод последовательной безусловной минимизации.

5.1. Метод последовательной безусловной минимизации. Этот метод основан на идее сведения исходной задачи (5.1) к последовательности задач безусловной минимизации:

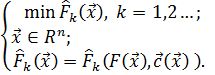, (5.3)

При этом

Количество итераций определяется в процессе выполнения соответствующего алгоритма следующим условием:

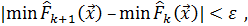
где – наперед заданная величина.

Последовательность целевых функций выбирается в виде:

, (5.4)

В качестве функций используются так называемые барьерные (внутренние штрафные) или штрафные (внешние штрафные) функции.

Барьерные функции ограничивают область поиска областью допустимых значений, возводя вдоль ее границы внутри области допустимых D значений барьер. Для этого к исходной целевой функции внутри области D добавляют положительную функцию 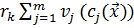, возрастающую по мере приближения к границе этой области. Поэтому метод, использующий барьерные функции получил также название «метод внутренней точки». Именно этот метод его авторы – Фиакко и Мак-Кормик собственно и назвали методом последовательной безусловной минимизации.

Штрафные функции напротив, разрешают поиск вне области допустимых значений D, но делают точки вне D «невыгодными», добавляя к значению исходной целевой функции вне области допустимых значений D положительную функцию 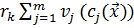. Этот метод получил название «метод внешней точки».

Барьерные или штрафные функции мы используем, определяется выбором вида функций . Крутизной «барьера» или «штрафа» вблизи границы области допустимых значений управляют с помощью последовательности значений параметра .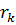

Ключевой идеей метода является последовательная безусловная минимизация целевых функций причем в качестве начального приближения на k -й итерации 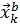используется результат поиска минимума на k- 1-й итерации .

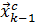Предполагается, что чем меньше номер итерации k, тем менее крутой «овраг» образуют барьерные или штрафные функции вблизи границы области допустимых значений. Следовательно, чем меньше k, тем проще и быстрее можно решить соответствующую задачу безусловной минимизации. С другой стороны, последовательность 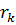выбирают так, чтобы с ростом величины k можно было бы получать все более точные решения. Для этого искажения значений целевой функции, вносимые барьерными функциями внутри области допустимых значений, должны уменьшаться. В случае же использования штрафных функций величина «штрафа» должна с ростом k все быстрее возрастать при удалении за пределы области допустимых значений.

Таким образом, получив хорошие приближения минимума при благоприятной структуре целевой функции для малых 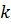, положение минимума последовательно уточняют на последующих итерациях.

Алгоритм 5.1 метода последовательной безусловной минимизации

1. Задать начальную точку , значение , предельное число итераций M;

2. Положить k =1

3. Выполнить безусловный поиск минимума целевой функции из начальной точки с результатом в точке 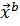и значением целевой функции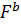

4. Для k от 2 до M с шагом +1 выполнять цикл

4.1. Выполнить безусловный поиск минимума целевой функции из начальной точки 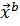с результатом в точке 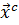и значением целевой функции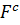

4.2. Если , выйти из цикла

4.3. Положить = ;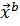

5. Если 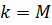, то вывести предупреждение, что минимум не достигнут

6. Положить результат решения задачи условной минимизации ;

7. Завершить работу

Барьерные функции обеспечивают возрастание целевых функций при приближении к границам области допустимых значений D. На границе этой области, в пределе, барьерные функции уводят значение целевой функции к

В качестве барьерных функций выбирают функции, удовлетворяющие следующему условию:

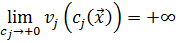
(5.5)

Обычно используют барьерные функции вида

(5.6)

При этом последовательность 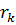выбирают в виде:

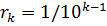, (5.7)

Основными преимуществами барьерных функций являются:

- дифференцируемость в области D целевых функций в случае, когда в этой области дифференцируемы и ;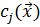

- поиск проходит только в области допустимых значений D, не затрагивая точки вне этой области и, таким образом, не требуя существования целевой функции за пределами области D.

Основные недостатки барьерных функций:

- начальное приближение для поиска необходимо выбрать лежащим в области допустимых значений, что не всегда удобно, особенно в случае нелинейных ограничений и ограничений-равенств;

- необходимо предпринимать специальные меры, чтобы в процессе поиска минимума не «проскочить» через барьер в область недопустимых значений варьируемых параметров;

- даже если решение задачи с ограничениями лежит не на границе, а внутри области допустимых значений, для того, чтобы найти решение с приемлемой точностью, придется выполнить достаточно большое число итераций, уменьшая 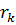, так как барьерные функции изменяют значение по сравнению с во всей области допустимых значений D (тем меньше внутри D, чем больше k).

Штрафные функции обеспечивают совпадение с исходной целевой функцией в области допустимых значений. Они обеспечивают ее увеличение за границами этой области, налагая «щтраф» в виде добавляемой к положительной функции. Штрафные функции должны удовлетворять следующим условиям:

(5.8)

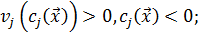
В качестве штрафных функций можно взять

(5.7)

В области допустимых значений, когда , эта функция принимает нулевое значение. За пределами области D, ее значение равно 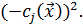Последовательность 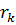выбирают в виде:

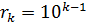. (5.8)

Штрафные функции имеют следующие преимущества:

- начальная точка поиска не обязательно должна лежать внутри области допустимых значений;

- если решение задачи условной минимизации лежит не на границе, а внутри области допустимых значений, решение будет найдено за две итерации алгоритма последовательной безусловной минимизации.

Основные недостатки штрафных функций:

- целевые функции , как правило, недифференцируемы на границе области D;

- так как поиск решения может проходить и за пределами области D, целевая функция и функции ограничения должны быть определены за пределами D.

Поиск по сайту: