Теория метода и описание установки. Дифракция Фраунгофера и интерференционный опыт Юнга с лазерным излучением

Лабораторная работа № 10

Дифракция Фраунгофера и интерференционный опыт Юнга с лазерным излучением.

Цель работы: изучение явления дифракции, интерференционного опыта Юнга с лазерным источником света;

определение ширины щели, расстояния между щелями и радиуса мелких круглых частиц по дифракционной картине.

Оборудование: гелий-неоновый лазер с блоком питания, зеркало со щелями, экран для наблюдения явлений дифракции и интерференции, линейка.

Теория метода и описание установки

Схема экспериментальной установки приведена на рис. 1. He-Ne лазер Л с блоком питания БП является источником с высокой пространственной и временной когерентностью излучения в красной видимой области спектра (λ=0,6328 мкм). На пути луча, вблизи лазера устанавливается горизонтальный столик-подставка П, где в ходе работы устанавливается либо непрозрачный экран со щелями 3, либо пластинка с частицами ликоподия.

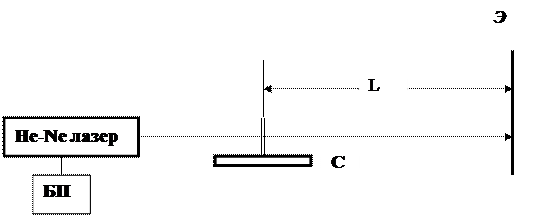
Рис. 1. Схема экспериментальной установки. БП – блок питания, С – столик, Э – экран.

Рис. 2. Геометрия расположения минимумов и максимумов распределения интенсивности света на экране.

Размещение объектов облучения по отношению к лазерному лучу осуществляется микрометрической подачей столика С (рис. 1). На расстоянии около L=1м от объекта З помешается экран Э с миллиметровой шкалой, на котором наблюдаются дифракционная картина от различных объектов. При освещении преграды З со щелями наблюдают дифракцию Фраунгофера в параллельных лучах.

Непрозрачная преграда 3 представляет собой стеклянную пластинку, покрытую слоем металлического алюминия, на поверхности которого прорезаны три тонкие щели. Таким образом, зеркало является непрозрачным экраном с прозрачными узкими щелями. Из трех щелей одна значительно удалена от двух других, чтобы можно было изучать явления происходящие при прохождении лазерного излучения через одну щель и через две (близкие) щели, расстояние между которыми меньше диаметра лазерного светового пучка.

1. Дифракционная картина от одной щели представляет собой распределение интенсивности света на экране в виде чередующихся освещенных (красных) и неосвещенных (темных) участков на экране, т.е. максимумов и минимумов. Наиболее интенсивный и широкий - центральный максимум (нулевого порядка, i=0). Дифракционные максимумы более высоких порядков слабо выражены, поскольку имеют малую интенсивность.

Угол дифракции 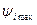, соответствующий i -му максимуму интенсивности, начиная с максимумов первого порядка ( = ± 1), связан с шириной щели b условием (2):

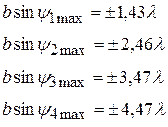(1)

где - длина волны излучения. Угол дифракции , соответствующий i -му минимуму интенсивности светa, связан с шириной щели b соотношением

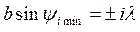(2)

где i = 1,2,3,... Из условий (I) и (2), определив углы дифракции максимумов и минимумов различных порядков, можно рассчитать ширину щели b по формулам:

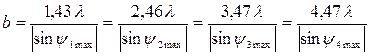(3)

и

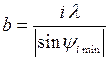. (4)

Углы дифракции размеры и можно выразить через расстояния и 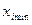от центра картины до максимумов и минимумов разных порядков i и расстояние L от преграды З и экрана Э (рис. 1):

(5)

и

, (6)

где L - расстояние от зеркала со щелями до экрана (рис.2). Подставляя в (3) и (4) значения 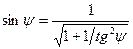, получим следующие выражения для нахождения ширины щели b

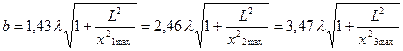(7)

и

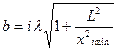. (8)

2. При освещении двух параллельных узких щелей светом от протяженного источника на экране можно наблюдать интерференционную картину – систему светлых и темных полос (опыт Юнга). Если источник позволяет наблюдать контрастную интерференционную картину, то такой источник света обладает пространственной когерентностью. Излучение He-Ne лазера характеризуется высокой пространственной (слабая расходимость пучка света) и высокой временной когерентностью вследствие высокой монохоматичности излучения.

При наблюдении дифракции от двух щелей дифракционные максимумы всех порядков (рис. 2) на экране перекрываются системой светлых и темных полос. Это и есть эффект интерференции света от двух щелей, доказывающий пространственную когерентность лазерного излучения.

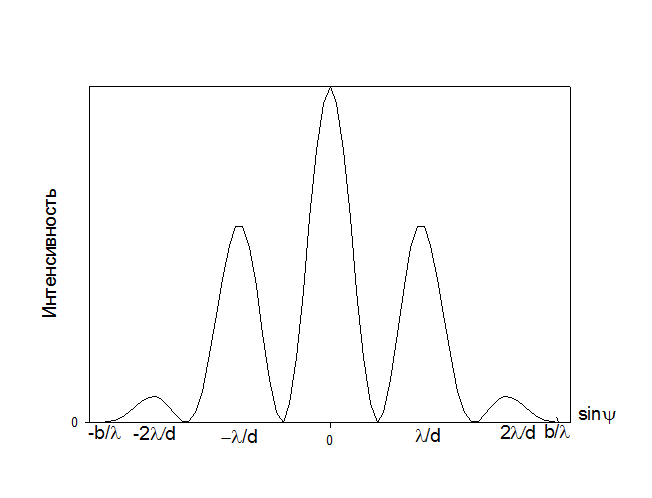
Рис.3. Распределение интенсивности при дифракции монохроматической волны при дифракции на N=2 щелях шириной b=0.4d

Интерференционная картина особенно отчетлива выражена на центральном дифракционном максимуме (рис.3). Углы, под которыми наблюдаются максимумы и минимумы интерференционной картины, зависят от расстояния d между щелями. Определить его проще всего из условий максимумов и минимумов интерференционной картины, расположенной в пределах одного центрального дифракционного максимума.

Угол , соответствующий j -му максимуму интерференционной картины, определяется соотношением:

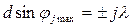. (9)

Угол 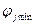, соответствующий j -ой темной полосе интерференционной картины, определяется соотношением:

, (10)

где 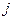= 0, 1, 2, 3...- порядок минимума или максимума.

Для максимума нулевого порядка можно приближенно принять . Тогда расстояние между щелями определится из условий:

(11)

и

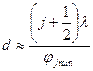. (12)

Если найти углы и - между соседними максимумами и минимумами, условия (11) и (12) изменятся следующим образом:

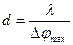(13)

и

. (14)

Разность 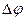можно выразить через линейное расстояние 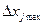и 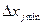между центрами соседних светлых и темных полос, соответственно:

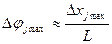(15)

и

, (16)

Условия (13), (14) преобразуются к виду:

(17)

и

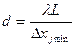. (18)

3. Если на столике С вместо преграды со щелями установить стеклянную пластинку с частицами ликоподия (спорами растения плауна), можно наблюдать дифракцию Фраунгофера на круглых частицах (рис. 1).

Для того чтобы углы дифракции на них были значительными размер частиц должен быть малым. Если на пути светового пучка поместить одну малую частицу, то даваемую ею на удаленном экране дифракционную картину наблюдать будет трудно, т.к. она проектируется на общий светлый фон пучка. Если же поместить на пути параллельного светового пучка множество одинаковых частиц, то каждая из них даст одинаковое угловое распределение света, независимо от ее положения в плоскости поперечного сечения пучка. При хаотическом расположении этих частиц в силу равной вероятности всех значений фаз дифрагированных по каждому направлению волн это распределение не нарушится интерференционными эффектами. В результате будут, складываться интенсивности световых пучков, дифрагировавших на разных частицах, и дифракционная картина усилится в N раз по интенсивности (где N - число частиц на пути светового пучка) по сравнению с картиной от отдельной частицы.

Частицы ликоподия представляют собой желтого оттенка шарики одинакового малого размера. Пластинка с ними выглядит матовой, светло-желтого цвета.

Дифракционная картина на экране в этом случае представляет собой систему концентрических темных и светлых (красных) дифракционных колец, окружающих светлый круг. При непосредственном (без объектива) наблюдении колец на экране они получаются достаточно широкими и сравнительно слабыми по интенсивности, так что для отчетливого их наблюдения требуется затемнение в помещении.

Угловые размеры дифракционных колец зависят от радиуса r частиц ликоподия следующим образом:

для светлых колец:

(19)

для темных колец:

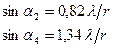, (20)

где - угловые радиусы светлых колец;

- темных колец; нумерация начинается с первого темного кольца, окружающего центральный светлый круг. Измерив, углы sina_i, можно из условий (19) и (20) определить радиус r частиц, вызвавших дифракцию:

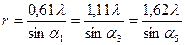(21)

и

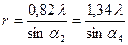. (22)

Очевидно, что где D_i - диаметр соответствующего дифракционного кольца на экране, а L - расстояние от пластинки с частицами ликоподия до экрана. Для удобства измерения диаметров колец можно начертить на экране ряд концентричных с ними окружностей. Заменив в (21) и (22) 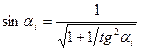, получим следующие выражения для:

(23)

и

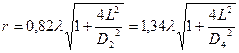, (24)

где - диаметры светлых колец,

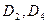- диаметры темных колец.

Поиск по сайту: