Линейное программирование. Задача линейного программирования – это задача математического программирования, в которой целевая функция и функции

Задача линейного программирования – это задача математического программирования, в которой целевая функция и функции, используемые в ограничениях, являются линейными. Основная задача линейного программирования записывается в виде:

(3.1.1)

Здесь целевая функция представляет собой скалярное произведение

(3.1.2)

векторов и , – матрица размерности :

(3.1.3)

– вектор-столбец: (T – символ транспонирования),

– n -мерное вещественное линейное пространство. Векторы , , матрица известны. Требуется найти хотя бы один вектор , принадлежащий допустимому множеству задачи (3.1.1)

,

доставляющий минимум функции (функционалу) .

Задача №1. Планирование производства

Исходные данные:

n – число видов производимых товаров;

m – число видов имеющихся ресурсов;

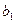– имеющееся количество единиц ресурса 1-го вида;

……………………………………………………………….

– имеющееся количество единиц ресурса m -го вида;

– количество единиц ресурса i -го вида, требуемое для производства единицы товара j -го вида;

– стоимость (иначе – доход от реализации) единицы товара j -го вида.

Требуется найти стратегию, т.е. определить, сколько товаров каждого вида надо производить, чтобы обеспечить максимальный валовый доход от реализации. Искомую стратегию будем рассматривать в виде набора , где 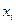– количество товаров i -го вида, которое необходимо производить (i=1,…,n).

Целевой функцией 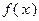является валовый доход

,

а условиями

С учетом изложенного, задача может быть сформулирована в виде:

;

и относится к классу задач линейного программирования.

Задача линейного программирования – это задача математического программирования, в которой целевая функция и функции, используемые в ограничениях, являются линейными. Основная задача линейного программирования записывается в виде:

Задача № 2

Данная задача является канонической, ;

, , , ,

– целевая функция.

Выбрав и в качестве свободных переменных, из системы находим:

(3.1.4)

Подстановка этих выражений в целевую функцию дает:

Отбросив константу -38, сформулируем задачу для двух переменных и :

(3.1.5)

Неравенства в этой задаче образуют систему, графическое решение которой представляет собой пятиугольник ABCDE, показанный на

рис. 2.1.1. Это и есть допустимое множество решений рассматриваемой задачи линейного программирования. Рассмотрим уравнение

(3.1.6)

Для решения задачи (3.1.5) необходимо найти такое максимальное значение , при котором пересечение прямой (3.1.6) с допустимым множеством не пусто. В подобных задачах среди множества решений обязательно будет по крайней мере одна вершина многоугольника, представляющего собой допустимое множество решений задачи. При увеличении прямая (3.1.6) перемещается в направлении вектора с координатами (6,15), сохраняя ортогональность с этим вектором. На рис. 2.1.1 показано конечное положение прямой (3.1.6), при котором ее пересечение с пятиугольником ABCDE не пусто. Оно соответствует значению 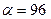, при этом пересечением является точка C. Решением задачи (3.1.5) являются координаты точки C: , . Их подстановка в выражения (3.1.4) позволяет найти значения остальных координат искомого решения исходной задачи: , .

Запишем найденное решение в виде: . При этом .

Поиск по сайту: