 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Глава 2. Динамическое программирование
|
Читайте также: |
Специфика метода динамического программирования заключается в том, что для отыскания оптимального решения задачи последняя разбивается на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования становится многошаговым. Термин «динамическое программирование» относится скорее к вычислительному методу, чем к особому типу задач. Многие задачи статического характера оказывается возможным сформулировать и решать как задачи динамического программирования. В то же время некоторые динамические задачи успешно решаются методами линейного и нелинейного программирования.
Покажем принцип метода динамического программирования на модели эффективного использования ресурсов.
Имеется некоторое количество ресурса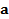 
, которое можно использовать 
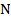различными способами. Пусть 
– количество ресурса, используемое 
-м способом,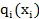 
– доход от использования ресурса -м способом (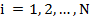
). Требуется распределить общее количество ресурса 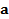между различными способами, чтобы суммарный доход был максимальным. Математически задача выразится следующим образом.
Найти
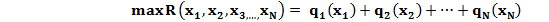(10.1)
при условиях:
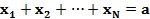
(10.2 )
Вместо одной задачи с данным количеством ресурса и фиксированным числом способов рассматриваем целое семейство таких задач, в которых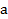 
принимает любые положительные значения и 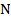– любые целые. Развертываем процесс во времени, производим распределение ресурсов в каждую единицу времени.
Зададим последовательность функций 
, определенных для 
следующим образом:
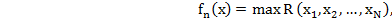(10.3 )
где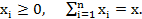 
Очевидно,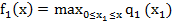 
Существует рекуррентное соотношение
(10.4 )
для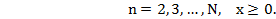 
Вывод этого соотношения основан на принципе оптимальности Беллмана.
Очевидно, 
Соотношения (10.4) позволяют заменить вычисление максимума по N переменным в исходной задаче решением N задач, в каждой из которых максимум находится лишь по одной переменной.
Примечания.
1. Наряду с решением исходной задачи получают решения целого семейства сходных между собой задач.
2. Та же идея построения рекуррентных соотношений может быть использована в случае нескольких видов ресурсов, но с увеличением размерности быстро растет объем вычислений.
Схема решения задачи [10.1] –[10.2]
1. Находят функции 
и 
.
2. Строят рекуррентное соотношение.
3. Находят функци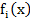и 
и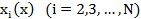 
.
4. Выбирают значения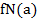 
– максимальное значение целевой функции 
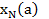- значение переменной 
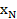в решении.
5. Остальные переменные получают следующие значения:
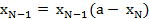
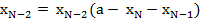
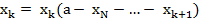
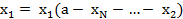
Пример
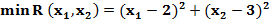
при условиях:
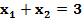
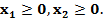
Решение. Для построения рекуррентного соотношения обозначим 
, 
. Построим последовательность функций
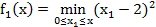
Легко видеть, что при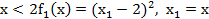 
, а при 
.
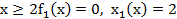Запишем значения функций и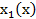 
при дискретных целых значениях 
из заданного интервала
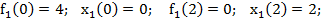
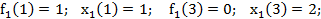
Построим рекуррентное соотношение, связывающее функци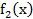и 
и :
Поскольку записать данную функцию в явном виде сложно, вычислим ее значения при дискретных значениях х:
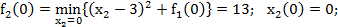
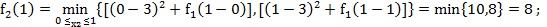
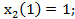
Здесь минимальное значение выбрано из двух выражений – пр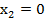и 
и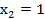 
и достигается при 
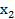=1.
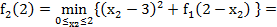
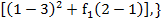
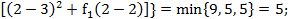
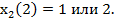
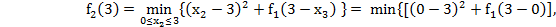
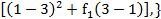
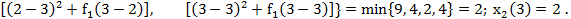
Находим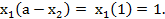 
Следовательно, решение данной задачи следующее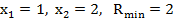 
.
Поиск по сайту: