Пример. Отбросим пока условие целочисленности (*) и решим задачу ЛП

(1)

Отбросим пока условие целочисленности (*) и решим задачу ЛП

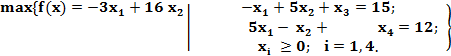(2)

Задача ЛП – каноническая.

Исходная таблица

B	Свободный член	Коэффициенты при неизвестных

Итерация 1

B	Свободный член	Коэффициенты при неизвестных

Итерация 2

B	Свободный член	Коэффициенты при неизвестных

План: 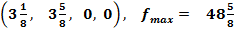оказался нецелочисленным. Для отыскания целочисленного плана применим метод Гомори (метод отсечений). С этой целью из завершающей симплексной таблицы выпишем каноническую систему (3) (эквивалентная системе (2)):

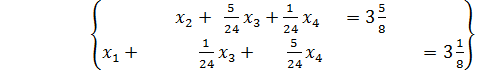(3)

Свободные члены обоих уравнений дробные. Выбираем первое уравнение (с наибольшим дробным свободным членом):

Рассмотрим неравенство (т. н. неравенство Гомори)

(3)*

Запишем (с положительным свободным членом)

. (3)**

В [4, с. 173] показано, что любой целочисленный план задачи (2) удовлетворяет и неравенству (3)*. Оптимальный же (нецелочисленный) план задачи (2) не удовлетворяет неравенству (3)*. Добавим неравенство (3)** к условиям задачи (2), то есть:

,

а т.к. системы были эквивалентны, то задача ЛЦП запишется ((3) +(3)**):

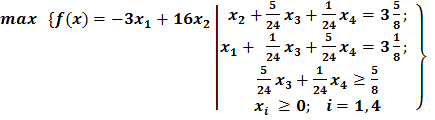(4)

Задача (4) почти каноническая ( =1,2,3….).

Решая задачу, получим оптимальный план

Замечание 1. Ясно, что всякое дополнительное ограничение сужает область допустимых значений и максимум может быть только меньше или равен, но никак не больше. Оптимальный нецелочисленный план при этом отсекается. Если бы при решении задачи (4) план получился бы нецелочисленным, то необходимо вновь выписать неравенство Гомори к канонической системе из последней симплексной таблицы (новой) и далее вновь решать задачу ЛП и т.д., пока план оптимальной не окажется целочисленным.

Замечание 2. Если левая часть уравнения системы имеет дробные часть равные 0, а правая часть дробная, то задача ЛЦП планов не имеет, например

. Здесь при целых значениях неизвестных никак не получится дробь , т.е. неизвестные нецелочисленны, поэтому для составления неравенства Гомори берем уравнения с дробной левой частью.

Замечание 3. Ранее, когда решали задачу ЛП оптимальный план был:

. Сейчас получили

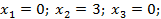
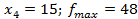. Если бы не применили для решения задачи ЛЦП метод Гомори, а просто округлили бы, глядя на решение задачи ЛП, например, , ; или или , то эти планы вообще выходят за пределы множества планов, т.к. не удовлетворяют системе задачи (1), в частности, системе

Ну, а если округлить , , то хотя это и план, но f(x) = 39, а у нас 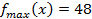, т.е. значения f(x) значительно отличаются.

Пример. Найти

при условиях:

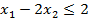
Снимем условие целочисленности.

Max Z = x1 + 2 x2

при условиях: x₁ - 2 x₂ + x₃ = 2

- 2x₁ + x₂ + x₄ =2

x₁ + x₂ + x₅ =3

.

Исходная симплексная таблица

Базисные переменные	Свободные члены ()	Коэффициенты при неизвестных
			-2
		-2
Z		-1	-2

Итерация 1

Базисные переменные	Свободные члены ()	Коэффициенты при неизвестных
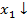
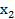
		-3
		-2
					-1
Z		-5

Итерация 2

Базисные переменные	Свободные члены ()	Коэффициенты при неизвестных
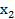
Z	= 5

Задача ЛП решена. Решение нецелочиcленное.

В таблице (7.3) получен оптимальный план. В столбце не все элементы целые. Так как во второй строке в содержится наибольшая дробная часть, то для нее составляют дополнительное ограничение, коэффициенты которого следующие:

или

Добавляем неравенство Гомори к итерации 2. Получим задачу ЦЛП:

Max Z = x₁ + 2 x₂

при условиях: x₃ + x₄ + x₅ = 7

x₂ + x₄ + x₅ =

x₁ - x₄ + x₅ =

- x₄ - x_{5 ≤}

.

.

Исходная симплексная таблица

Базисные переменные	Свободные члены ()	Коэффициенты при неизвестных
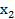
					S2
S2
Z	= 5

Итерация 1

Базисные переменные	Свободные члены ()	Коэффициенты при неизвестных	S2
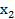
						-1
							-1
S2							-3
Z

Получили оптимальное и целочисленное решение

L(max) = 5. Дадим геометрическую интерпретацию решения данной задачи. Из рис. 1 видно, что максимально значение целевая функция принимает в точке , то есть решение является оптимальным, но без учета требования целочисленности.

Рис. 1

С учетом требования целочисленности решение не является оптимальным, поэтому используем дополнительное ограничение

или . Значения переменных x4 и x5 подставим из второго и третьего уравнений системы ограничений , 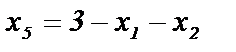. В результате получим . Этому неравенству на рис. 1 соответствует полуплоскость, ограниченная прямой , отсекающей от многоугольника допустимых решений треугольник АДА*. В новом многоугольнике допустимых решений ОДА*ВС найдем точку А*(1,2), в которой целевая функция принимает максимальное значение. Так как координаты точки А* – целые числа, то решение 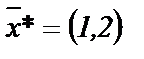является оптимальным планом исходной задачи.

§2. Пример постановки задачи рационального раскроя [4, c.176].

Пусть имеется достаточно большое количество брёвен длиной 3 м. Брёвна следует распилить на заготовки двух видов: длиной 1,2 м. и 0,9м.; причем заготовок каждого вида должно быть получено не менее 50 шт. и 81 шт. соответственно. Каждое бревно может быть распилено на указанные заготовки несколькими способами. Требуется найти число брёвен, распиливаемых каждым способом с тем, чтобы необходимое количество заготовок каждого вида было получено из наименьшего количества бревен.

Решение. Бревно, длиной 3м может быть распилено на заготовки нужной длины следующими способами:

1).На 2 заготовки длиной 1,2м;

2). На 1 заготовку длиной 1,2м и 2 заготовки длиной 0,9м;

3). На 3 заготовки длиной 0,9м.

Другие способы раскроя, очевидно, не следует принимать во внимание.

Пусть x₁, x₂, x₃ – число бревен, распиливаемых 1, 2 и 3 способами соответственно (т.е. x₁,x₂,x₃ – целые неотрицательные числа).

Всего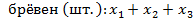

Надо найти

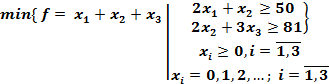
Ответ: . Для того, чтобы получить необходимое количество заготовок каждого вида надо 7 бревен распилить первым способом; 36 - вторым; 3 – третьим. То есть получили:

2*7 +36 =50;

2*36 +3*3=81.

Решение:

Надо ввести искусственный базис, для этого проделаем тождественное преобразование: уравнение с большей правой частью (81) вычтем из 1-го уравнения и сменим знаки на противоположные:

;

;

.

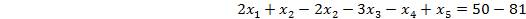Получим задачу:

Вводим искусственное переменное (во втором уравнении), решаем вспомогательную задачу и т.д.

Поиск по сайту: