АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Общая задача выпуклого программирования заключается в минимизации функции

Читайте также:
  1. Data Mining и Business Intelligence. Многомерные представления Data Mining. Data Mining: общая классификация. Функциональные возможности Data Mining.
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. I Психологические принципы, задачи и функции социальной работы
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 3.1. Двойственная задача линейного программирования
  6. I. Деньги и их функции.
  7. I. Общая установка сознания
  8. I. Общая характеристика.
  9. I. Функции
  10. I. Функции эндоплазматической сети.
  11. I.5.3. Подготовка данных для задачи линейного программирования
  12. I.5.4. Решение задачи линейного программирования

при условиях:

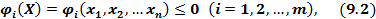
то есть в отыскании средних точек области решений Ω такой точки 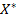, для которой

где 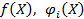– выпуклые гладкие функции.

Приведем общую задачу к каноническому виду. С этой целью в задачу выпуклого программирования вводится дополнительная переменная 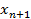и дополнительное ограничение

 

Тогда задача (9.1) - (9.2) будет эквивалентной задаче минимизации линейной формы

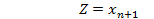
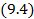
при ограничениях:

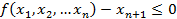
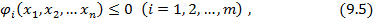
которая называется канонической.

Или

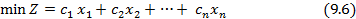
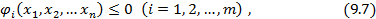
где функции – гладкие и выпуклые. Для решения задачи (9.1) - (9.2) и, следовательно, (9.4) - (9.5) можно использовать метод наискорейшего спуска.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)