при ограничении

(*)

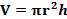причем г и 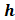— соответственно радиус емкости и ее высота. В данном случае ограничение (*) может быть представлено в виде неравенства

,

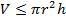которое записывается в виде позиномиального ограничения:

.

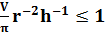Вводя обозначения:

,

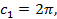
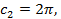
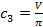
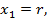
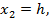
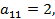
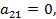
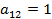
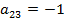запишем поставленную задачу в стандартной форме обозначений позиномов:

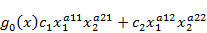(1)

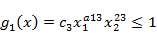(2)

Матрица коэффицентов 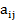будет:

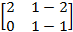
и, как нетрудно убедиться, имеет ранг, равный 2, т. е. в задаче есть две независимые переменные (n' = 2). Число членов в позиномах (1) и (2) равно 3 (m = 3), поэтому степень трудности задачи в соответствии с выражением (X, 51) составляет:

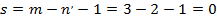
Выражение для двойственной функции в данном случае имеет вид:

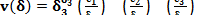(3)

поскольку

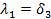
так как ограничение представляет собой одночленный позином. Условие нормализации при этом записывается как

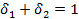
и совместно с условиями ортогональности:

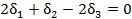
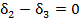
составляет систему трех уравнений относительно трех неизвестных .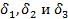

Решением системы уравнений будет:

,

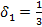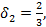
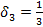
Подстановка значений 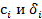- в выражение двойственной функ­ции (3) дает соотношение

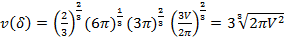
которое и определяет минимальное значение поверхности S. Следующий этап решения задачи заключается в определении размеров емкости.

Окончательно получим:

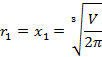
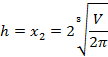
т. е. найдено в точности то же самое решение, которое было опре­делено при использовании метода множителей Лагранжа.

Литература

1. С. Гасс. Линейное програм мирование, пер. с англ.М.,"Физматгиз", 1961.

2. Ф. И.Карпелевич, Л.Е.Садовский. Элементы линейной алгебры и линейного программирования, М.,"Наука", 1967.

3. П. Е.Данко,А.Г.Попов. Высшая математика в упражнениях и задачах ч. 11, М.,"Высшая школа", 1999.

4. Пинскер А.Г.,Брыжина Э.Ф. Основы оптимального программирования, Л. 1974.

5. Калихман И.А. Сборник задач по математическому програм­мированию. «Высшая школа», 1975.

6. Т.Ф. Гуревич В.О. Лущук. Сборник задач по математическому програм­мированию. Москва «Колос», 1977.

7. Грешилов А.А. Прикладные задачи математического программирования: учеб. пособие для студ. втузов / Грешилов, Анатолий Антонович. - 2-е изд., доп. - М.: Логос, 2006.
8. Логинова И.В. Методы оптимизации: учебно-методич. пособие / И. В. Логинова, М. С. Мищенко; Казан. гос. технол. ун-т. - Казань, 2008.
9. Пантелеев С.Д. Математическое программирование и экономические задачи: учеб. пособие / Пантелеев, Сергей Дмитриевич. - М.: Изд-во МГОУ, 2007.
10. Хуснутдинов Р.Ш. Практикум по линейной алгебре и линейному программированию: учеб. пособие / Казан. гос. технол. ун-т. - Казань, 2009.
11. Бозиев С. Н. MATLAB 2006 а в примерах / Бозиев, Садин Назирович; Рос. гос. ун-т нефти и газа. - М., 2006.
12. Бояринов А. И., Кафаров В. В. Методы оптимизации в химической технологии. Изд. 2-е. М., «Химия» 1975.

13. Монахов В. М. и др. Методы оптимизации. Применение математических методов в экономике. Пособие для учителей. М., «Про­свещение», 1978. 175 с.

Оглавление

Методы оптимизации Введение.
§1. Этапы решения задачи
§2. Некоторые сведения из линейной алгебры.
Матрицы.
Определители.
§3. Классификация методов математического программирования.
Сравнительная характеристика методов решения задач оптимизации.
§4. Методы исследования функций классического анализа
4.1 Необходимые и достаточные условия безусловного экстремума функции. 1). Функция у = f (х) (одной переменной).   2) Функция у = f () (нескольких переменных).
2). Функция у = f () (нескольких переменных).
4.2. Необходимые и достаточные условия условного экстремума. Принцип Лагранжа.
§5. Методы исследования функций численного анализа.
Раздел 1. Линейное программирование.
Глава 1.Метод линейного программирования. Сведение общей задачи ЛП к равносильной ей основной задаче путём введения добавочных неизвестных.
§1. Примеры составления задач ЛП.
Формулировка задачи о рациональном питании.
Формулировка транспортной задачи
Аналитическая идея симплексного метода
§ 2. Геометрическая интерпретация решения задачи ЛП.
§ 3. Алгоритм решения канонической задачи ЛП симплексным методом (метод Данцига).
Алгоритм решения канонической задачи ЛП симплексным методом (общий случай).
§ 4. Решение почти канонических задач.
§ 5. Вырожденная задача ЛП.
Глава 2. Решение основной задачи линейного программирования   §1 Сведение основной задачи к двум каноническим. Метод искусственного базиса
§2. Задача о диете
Глава 3. Целочисленное линейное программирование.
§1 Метод Гомори
§2. Пример постановки задачи рационального раскроя.
Глава 4. Теория двойственности в ЛП.
§ 1. Симметричные двойственные задачи. Задача об использовании сырья.
§2. Несимметричные двойственные задачи.
Глава 5. Примеры задач оптимизации.
§1. Решить задачи оптимизации графическим методом (1-7).
§2. Решить задачи оптимизации симплексным методом (8 – 34).
§3. Используя метод искусственного базиса для нахождения исходного опорного плана, решить следующие задачи (35 – 52).
§4. Найти целочисленное решение задач оптимизации (53 – 62).
Раздел 2. Нелинейное программирование
Глава 1. § 1. Задачи нелинейного программирования с линейной целевой функцией и нелинейной системой ограничений.
§ 2. Задачи нелинейного программирования с линейной системой ограничений, но нелинейной целевой функцией.
Решение задач дробно-линейного программирования симплексным методом
§ 3. Задачи нелинейного программирования с нелинейной системой ограничений и нелинейной целевой функцией.
§4. Градиентный метод нелинейного программирования
§5. Выпуклое программирование.
Квадратичное программирование.
Геометрическая интерпретация и графический способ решения задачи квадратичного программирования
§6. Параметрическое программирование.
Глава 2.Динамическое программирование.
Глава 3.Метод случайных испытаний.
Глава 4.Геометрическое программирование.
Литература	9

Поиск по сайту: