Глава 3. Метод случайных испытаний

Пусть каким-то способом выбрано п случайных чисел. При­нимаем эти числа за значения переменных х₁, х_2…..., х_п, проверяем допустимость такого решения и вычисляем для него значение целевой функции. Такой процесс повторяем много­кратно, фиксируя точку в том случае, если целевая функция в ней достигает лучшего по сравнению с предыдущим значения (в смысле приближения к оптимуму). Общее число случайных проб зависит от числа переменных, требуемой точности искомых величин и заданной вероятности получения оптимального решения. Все это определяется зара­нее. Поиск прекращается, когда число испытанных точек до­стигнет расчётного. Точку с наибольшим (наименьшим) значе­нием целевой функции считаем оптимальной. Метод случайных испытаний может быть реализован только на ЭВМ, причем интересно отметить, что случайные числа ЭВМ вырабатывает сама

Глава 4. Геометрическое программирование.

Рассмотренные выше методы нелинейного программиро­вания предназначены для решения задач оптимизации с критерием оптимальности, сформулированным как нелинейная функция неза­висимых переменных, на допустимую область изменения которых накладываются ограничения, имеющие вид равенств или нера­венств, возможно также нелинейного вида. Как правило, решение подобных задач методами нелинейного программирования требует значительного объема вычислений и сопряжено с определенными трудностями, обусловленными особенностями целевой функции и ограничений. Поэтому создание методов решения задач нелинейного про­граммирования, использующих специфический характер целевых функций и ограничений для построения эффективных вычислитель­ных схем, несомненно имеет большое практическое значение. К числу таких методов, интенсивно развиваемых в последние годы, относится метод геометрического программирования,

Основные понятия.

Метод геометрического программирования возник и разви­вался в связи с задачами инженерного проектирования и имеет целью решение задач оптимизации, в которых критерий оптималь­ности и ограничения на переменные представляются в виде поло­жительных полиномов, называемых также позиномами, вида:

причем 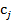— положительные константы, а показатели степени 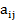— произвольные вещественные числа. Предполагается, что не­зависимые переменные принимают только поло­жительные значения.

В общем случае задача геометрического программирования за­ключается в

минимизации позинома при наличии ограни­чений

Позиномиальные выражения достаточно широко распростра­нены в науке и технике, примером чего являются известные крите­риальные соотношения, представляющие собой ни что иное как одночленные позиномы. Кроме того, во многих случаях позиномы могут использоваться для аппроксимации функциональных зави­симостей различной степени сложности, определяемых математи­ческими моделями или же свойствами рассматриваемых объектов. Таким образом, метод геометрического программирования может применяться во всех тех случаях, когда либо в самой поста­новке задачи присутствуют позиномиальные выражения, либо имеющиеся зависимости аппроксимируются позиномами.

Поиск по сайту: