 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачу решают в следующем порядке
1. Пользуясь симплекс-методом, решаем задачу (6.1) – (6.3) при 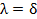 до получения оптимального плана.
до получения оптимального плана.
Коэффициенты линейной формы равны:
 (6.4)
(6.4)
Следовательно, для любого базиса разности  могут быть представлены в виде линейной функции от
могут быть представлены в виде линейной функции от  , то есть
, то есть
 (6.5)
(6.5)
Тогда
 (6.6)
(6.6)
что означает совместность всей системы неравенств
 (6.7)
(6.7)
Решение задачи (6.1) – (6.3), полученное при 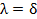 , является оптимальным для всех значений параметра
, является оптимальным для всех значений параметра  , удовлетворяющих условию
, удовлетворяющих условию 
| (6.8) |

| (6.9) |
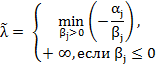
Здесь возможны следующие случаи:
а)  , процесс решения закончен. Полученный план при
, процесс решения закончен. Полученный план при 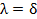 остается оптимальным для всех значений параметра
остается оптимальным для всех значений параметра 
б)  , при
, при  . Если все
. Если все  , то линейная форма (6.1) при
, то линейная форма (6.1) при  не ограничена снизу. Полученный план при
не ограничена снизу. Полученный план при 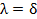 остается оптимальным для всех значений параметра
остается оптимальным для всех значений параметра  ;
;
в) 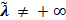 и существует по крайней мере одна
и существует по крайней мере одна  . В этом случае в базис вводится вектор
. В этом случае в базис вводится вектор  и исключается вектор
и исключается вектор  . Новый базис соответствует оптимальному плану хотя бы для одного значения параметра
. Новый базис соответствует оптимальному плану хотя бы для одного значения параметра  .
.
Если интервал  является полной совокупностью значений
является полной совокупностью значений  , для которых новый базис соответствует оптимальному плану, то
, для которых новый базис соответствует оптимальному плану, то 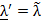 . Полученный оптимальный план при
. Полученный оптимальный план при 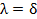 остается оптимальным для всех значений параметра
остается оптимальным для всех значений параметра  . Полагая далее
. Полагая далее 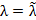 , продолжают процесс решения задачи. Аналогичным образом переходят от одного интервала изменения
, продолжают процесс решения задачи. Аналогичным образом переходят от одного интервала изменения  к другому, пока один из интервалов не включит
к другому, пока один из интервалов не включит  .
.
Величины  называют критическими значениями параметра
называют критическими значениями параметра  , а оптимальные планы, соответствующие различным значениям
, а оптимальные планы, соответствующие различным значениям  – критическими решениями.
– критическими решениями.
2. Пользуясь симплекс-методом, можно убедиться, что при 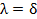 линейная форма не ограничена снизу на выпуклом множестве, определяемом условиями (6.2).
линейная форма не ограничена снизу на выпуклом множестве, определяемом условиями (6.2).
Здесь возможны следующие случаи:
а)  – вектор, подлежащий вводу в базис,
– вектор, подлежащий вводу в базис,  , все
, все 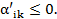 Если
Если  , то линейная форма задачи не ограничена снизу для любого
, то линейная форма задачи не ограничена снизу для любого 
б) если  , неравенство
, неравенство  будет иметь место для всех
будет иметь место для всех  , то есть для любого
, то есть для любого  задача не имеет оптимального плана. Если все
задача не имеет оптимального плана. Если все  , то оптимальный план задачи
, то оптимальный план задачи 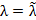 получен.
получен.
Пусть  , тогда этот план является решением задачи при
, тогда этот план является решением задачи при  , а далее решение продолжается так же, как в случае (а).
, а далее решение продолжается так же, как в случае (а).
Если не все  , в базис вводится любой вектор, для которого
, в базис вводится любой вектор, для которого 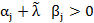 . Процесс продолжается до тех пор, пока не окажется, что
. Процесс продолжается до тех пор, пока не окажется, что  , или пока не будет обнаружен вектор
, или пока не будет обнаружен вектор  c
c  , все коэффициенты разложения которого по базису неположительны.
, все коэффициенты разложения которого по базису неположительны.
Если 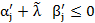 для всех j, встречаем случай (а).
для всех j, встречаем случай (а).
Если  , линейная форма задачи не ограничена снизу при всех
, линейная форма задачи не ограничена снизу при всех  .
.
Если  , то линейная форма при
, то линейная форма при 
 , где
, где  ’ >
’ >  , не ограничена снизу.
, не ограничена снизу.
Поиск по сайту: