АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Несимметричные двойственные задачи

Читайте также:
  1. А. Постановка транспортной задачи.
  2. Аналитический метод решения задачи.
  3. Аналитический метод решения задачи. Условия максимума функции одной переменной.
  4. Б. Математическая модель транспортной задачи.
  5. Биофизика – как наука. Практические задачи. Методы исследования
  6. Возникновение обществ содействия милиции, их правовое положение и задачи.
  7. Выберем поверхность интегрирования, учитывая симметрию задачи.
  8. Генетика, ее задачи. Наследственность и изменчивость – свойства организмов. Основные генетические понятия
  9. Государственная региональная политика: цели и задачи.
  10. Государственная туристическая политика и ее задачи.
  11. Двойственные задачи линейного программирования
  12. Двойственные задачи оптимизации.

 

Рассмотрение таких задач часто полезно в ЛП. Причём эти задачи сводятся к симметричным. Задача I – основная задача ЛП, задача II задача минимизации, но во II задаче могут быть любого знака.

Сведение осуществляется следующим образом. Как известно, равенство равносильно паре неравенств ; или . В задаче I каждое уравнение заменяется парой неравенств такого рода. Тогда задача I будет задачей максимизации с «n» переменными и «2m» неравенствами. Затем выписываем симметричную ей двойственную задачу. Например, дано:

Задача I Задача II
при условиях: Ответ: (2,3,0,0) при условиях: 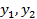– любого знака Ответ: (-1,-2),

 

Сведем к паре симметричных двойственных задач ЛП

 

Задача I Задача II
при условиях: при условиях:

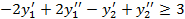
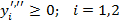
У задачи II, когда – любого знака, любой план называется псевдопланом.

Теорема: Если 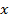* некоторый план задачи I, а * - некоторый псевдоплан задачи II и f(x*)=g(y*), то x* и y* оптимальные план и псевдоплан I и II задачи.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)