 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Двойственные задачи линейного программирования
С каждой задачей линейного программирования можно некоторым образом сопоставить другую задачу линейного программирования, называемую двойственной по отношению к исходной (прямой).
Прямая задача:


Двойственную задачу по отношению к прямой задаче составляют согласно правилам.
Целевая функция прямой задачи задается на максимум, тогда целевая функция двойственной задачи - на минимум, и наоборот.
Матрица

составленная из коэффициентов в системе ограничений прямой задачи, и аналогичная матрица

в двойственной задаче получаются друг из друга транспонированием. Число переменных в двойственной задаче (т) равно числу соотношений (ограничений) в прямой задаче, а число ограничений двойственной задачи (п) - числу переменных в прямой задаче.
Коэффициенты при неизвестных в целевой функции двойственной задачи - свободные члены (bi), а правые части в ограничениях двойственной задачи (сj) - коэффициенты при неизвестных в целевой функции прямой задачи.
Если переменная xj прямой задачи может принимать только положительные значения (хj≥ 0), то j -еусловие двойственной задачи - условие неравенства вида «≥». Если 1-е соотношение в прямой задаче - неравенство, то i -я переменная двойственной задачи zi≥ 0.
Если прямая задача имеет решение, то и двойственная задача тоже имеет решение, причем max(min) L1= min(max) L2, поэтому для отыскания оптимума достаточно решить одну какую-либо из задач двойственной пары. Обычно решают ту, которая проще.
Оптимальный план двойственной задачи позволяет оценить степень дефицитности ресурсов, потребляемых при выполнении оптимального плана исходной задачи.
Пример. Для производства изделий А, В, С используются три различных вида ресурсов. Каждый из видов ресурсов может быть использован в количестве, соответственно не большем 180, 210, 244 ед. Известны затраты каждого из видов ресурсов на ед. продукции и цена ед. продукции каждого вида (табл. 15).
Определить план производства, при котором обеспечивается максимальный доход, и оценить дефицитность каждого вида ресурсов, используемых для производства продукции.
Оценки, приписываемые каждому виду ресурсов, должны быть такими, чтобы оценка всех используемых ресурсов была минимальной, а суммарная оценка ресурсов на производство единицы продукции каждого вида - не меньше цены единицы продукции данного вида.
Решение. Обозначим через х1 искомый план производства изделий А, через х2 - В, x3 - С, а через z 1- двойственную оценку дефицитности первого вида ресурса, через z2 - второго, z3 - третьего.
Таблица 15
| Вид ресурса | Норма расхода ресурса на единицу продукции | ||
| А | В | С | |
| Цена продукции |
Тогда прямая и двойственная задачи формулируются:
· прямая задача
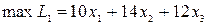

· двойственная задача


Решение прямой задачи дает оптимальный план производства изделий А, В, С, а решение двойственной задачи - оптимальную систему оценок ресурсов, используемых для производства этих изделий:

Исходя из анализа оптимальных двойственных оценок, можно сделать следующие выводы.
Ресурсы первого и третьего видов используются полностью. Полному использованию этих ресурсов соответствуют полученные оптимальные оценки  ,отличные от нуля, т. е. положительные двойственные оценки имеют ресурсы, полностью потребляемые при оптимальном плане производства. Значит, ресурс второго вида недоиспользуется (на 80 ед.).
,отличные от нуля, т. е. положительные двойственные оценки имеют ресурсы, полностью потребляемые при оптимальном плане производства. Значит, ресурс второго вида недоиспользуется (на 80 ед.).
Двойственные оценки определяют дефицитность используемых ресурсов. Величина двойственной оценки показывает, на сколько возрастает максимальное значение целевой функции прямой задачи при увеличении количества соответствующего ресурса на единицу.
Так, увеличение количества ресурса первого вида на 1 ед. приведет к тому, что появится возможность найти новый оптимальный план производства изделий, при котором общий доход возрастает на 5,75 д. е. и станет равным 1340 + 5,75 = 1345,75 д. е. Анализ полученных оптимальных значений новой прямой задачи показывает, что это увеличение общего дохода достигается за счет увеличения производства изделий В на 0,625 ед. и сокращения выпуска изделий С на 0,25 ед. Вследствие этого использование ресурса второго вида уменьшается на 0,125 ед.
Точно так же увеличение на 1 ед. количества ресурсов третьего вида позволит перейти к новому оптимальному плану производства, при котором доход возрастёт на 1,25 д. е. и составит 1340 + 1,25 = 1341,25 д. е., что достигается за счет увеличения выпуска изделий С на 0,25 ед, и уменьшения выпуска В на 0,25 ед., причем объем используемого ресурса, второго вида возрастает на 0,625 ед.
При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получаем:
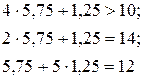
Первое ограничение выполняется как строгое неравенство, т. е. двойственная оценка всех ресурсов на производство единицы изделия А выше цены этого изделия и, следовательно, выпускать его невыгодно. Его производство и не предусмотрено оптимальным планом прямой задачи.
При одновременном изменении ресурсов всех видов на величину  можно оценить их суммарное влияние на значение целевой функции (при условии неизменности двойственных оценок в новой двойственной задаче относительно оценок в первоначальной двойственной задаче):
можно оценить их суммарное влияние на значение целевой функции (при условии неизменности двойственных оценок в новой двойственной задаче относительно оценок в первоначальной двойственной задаче):

где  - величина возможного (при сохранении оптимального плана первоначальной двойственной задачи) изменения (увеличения или уменьшения) ресурса i -го вида.
- величина возможного (при сохранении оптимального плана первоначальной двойственной задачи) изменения (увеличения или уменьшения) ресурса i -го вида.
Поиск по сайту: